Retrieving and Classifying Affective Images via Deep Metric Learning

论文标题：
Retrieving and Classifying Affective Images via Deep Metric Learning (基于深度学习的情感图像检索与分类)
论文地址：http://users.cs.cf.ac.uk/Yukun.Lai/papers/retrieving-classifying-affective-AAAI18.pdf

1、Introduction

Affective Image analysis(或Image sentiment analysis)，顾名思义，就是挖掘图像所蕴含的情感类别的任务。图像是一种直观的表达方式，当人们看到一张图片时，不仅会关注图像包含的物体，往往也会被图片传达的情绪所感染或冲击。因此，在某些实际场景中，仅对图像做分类、识别等研究是不够的。比如广告图中，图像所传达的情感是影响顾客倾向的重要方面。由此可见图像情感分析是一项具有广泛应用价值的任务。

本文作者认为先前的工作都只是将图像进行多分类，每一个标签都是独立的。然而实际上，情感标签不同于具体的对象类别标签，具有相同极性（即积极或消极）的情感标签是高度相关的。因此该任务本身具有模糊性，但很少有方法专注于利用情感的这种特性来理解情感图像。
于是，作者在传统的分类损失基础上，加入了相似度损失，利用图片所属情感标签之间的相似程度解决传统方式的缺陷。
本文使用The Mikels’ emotion wheel的八种情感划分作为标签。
如上图所示，图像的八种情感标签分别是：愉悦、满足、敬畏、激动、害怕、悲伤、厌恶、愤怒 。
文章的主要贡献有以下几个方面：

• 提出了一个多任务深度框架(multi-task deep framework)来优化检索和分类目标
• 针对相似度损失，在三重约束的基础上提出了情感约束(sentiment constraints)，能够探索情感标签的层次关系
• 利用情感向量(sentiment vector)作为一种有效的表示，利用来自卷积层的纹理表示(texture representation)来区分情感图像

2、Proposed Algorithm

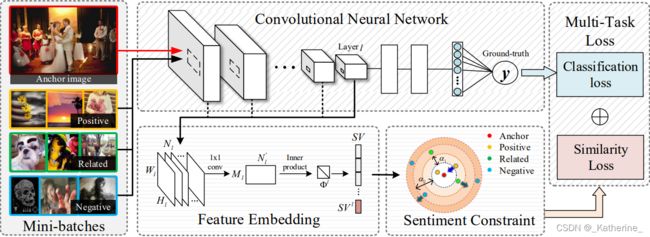
上图对所提出的算法进行了展示。对于包含不同情绪的图像的小批量，生成一个情绪向量(SV)来测量情绪差异。具体来说，使用1×1卷积层在降低特征映射维数的同时生成非线性激活，然后计算情感向量中每对特征映射之间的相关性。本文的框架同时优化了情感图像理解的分类损失和相似性损失。

Sentiment Metric Learning

使用图像的情感向量(SV)的欧氏距离表示图像之间的情感度量（SV将在下一节具体介绍）：
$$D(x_i,x_j)\to ||S{V}_i-S{V}_j|{|}_2^2$$ 其中$i$和$j$表示来自训练集$\Gamma$的不同图像，$S{V}_i$和$S{V}_j$指从卷积层计算出的情感向量。
不同情绪图像之间的距离可以说是主观的，但总体关系可以认为是明确的：具有相同极性的图像彼此接近，而具有相反极性的图像应该相距更远。
因此，将三重态约束推广到考虑情感关系的情感约束。

Triplet Constraints

算法通常生成小批量的三元组，即锚$a_i$、同一类的正实例$p_i$和不同类的负实例$n_i$。目标是学习一个嵌入函数，该函数将较小的距离分配给更相似的图像对，可以表示为：$$D(a_i,p_i)+\alpha <D(a_i,n_i)$$ $\alpha >0$是在正对和负对之间强制执行的边距。

Sentiment Constraints

情感标签之间存在层次关系，例如The Mikels’ emotion wheel八种情绪有四种积极情绪和四种消极情绪，即中上半圆的四种情绪()是同一个极性(积极)，下半圆的四种情绪是另一个极性(消极)。
本文作者基于上述情感之间的关系对图片进行三档划分：
对于每一张图片，将其视作锚定图片(archor image)，与它属于同一个情绪类别的图片记为正(positive)，与它属于同一极性其他类别的图片记为相关(relative)，与它情感极性不同的图片记作负(negative)
确保特定情绪的图像$a_i$(锚定)与完全相同情绪的所有图像$p_i$(正)更接近，这比具有相同极性情绪的任何相关图像$r_i$更接近，而具有相反极性$n_i$的图像保持最远的距离。
从形式上讲，情绪约束可以表示为
$$\{\begin{array}{l}{D}^{\ast }(a_i,p_i)+{\alpha }_1<D^{\ast }(a_i,r_i)\\ D^{\ast }(a_i,r_i)+{\alpha }_2<D^{\ast }(a_i,n_i)\end{array}$$ 其中 ${\alpha }_1,{\alpha }_2>0$
令y表示x对应的标签，$D^{\ast }(x_i,x_j)=\theta D(x_i,x_j)$, $\theta \propto \frac{1}{dis(y_i,y_j)}$,
$dis(y_i,y_j)$=1 + “the number of steps required
to reach one emotion from another by the Mikels’ wheel” (从一种情感到另一种情感所需的步数)。
通过上述公式，情绪约束能够利用自然的情绪关系，即情绪不仅可以分为两个极性，而是进一步根据情绪之间的距离决定相关性。
通过最小化情绪损失函数来学习情绪度量：$$\begin{gathered} E_{sml}=\sum _{i=1}^N[D^{\ast }(a_i,p_i)-D^{\ast }(a_i,r_i)+{\alpha }_1{]}_{+} \\ +\sum _{i=1}^N[D^{\ast }(a_i,r_i)-D^{\ast }(a_i,n_i)+{\alpha }_2{]}_{+} \end{gathered}$$ 其中N表示训练图片数量, $[\cdot {]}_{+}=max(\cdot ,0)$

Sentiment Vector for Feature Embedding

图像纹理(image texture)已被证明是与图像情感分类相关的重要视觉特征之一，为了有效地表示图像纹理，本文利用深度表示，提出了由多个Gram层组成的情感向量(SV)，每个Gram层计算卷积层中滤波器响应(filter responses)的内积。

具体地说，首先将图像输入CNN并计算每个中间卷积层$l\in \{1,2,\dots ,L\}$的响应。假设层$l$包含$N_l$个过滤器，因此包含$N_l$个特征映射(feature map)，每个映射的大小为$W_l\times H_l$。

由于CNN通常在一层中有几十个甚至更多的过滤器，因此Gram矩阵中会有数千个元素，这会导致沉重的计算负担。
为了提高该框架的泛化能力，采用1×1卷积层，在减小Gram矩阵大小的同时加入了非线性激活。
因此，层$l$中的响应可以存储在矩阵$F^l\in {\mathbb{R}}^{M_L\times N_L^{\prime }}$中，式中，$F_{ij}^l$是层$l$中位置$i$处第$j$个过滤器的激活。$N_L^{\prime }$是过滤器的数量，$M_L=W_L\times H_L$。
这些特征图可以表示为二维矩阵$\Phi \in {\mathbb{R}}^{N_L^{\prime }\times N_L^{\prime }}$, Gram矩阵中的每个元素表示每对特征映射(feature map)之间的相关性，${\Phi }_{ij}^l={\sum }_{k=1}^{M_L}{F}_{ki}^l{F}_{kj}^l$是层l中第i个和第j个矢量化特征映射之间的内积。
由于矩阵是对称的，独立元素个数有$N_L^{\prime }\times (N_L^{\prime }+1)$个，将来自层$l$的情感向量$SV$定义为:$$S{V}^l=[{\Phi }_{1,1}^l,{\Phi }_{2,1}^l,\dots ,{\Phi }_{N_L^{\prime },1}^l,\dots ,{\Phi }_{N_L^{\prime },N_L^{\prime }}^l]$$ 将来自多个卷积层的情感向量连接为$SV=[S{V}^1,S{V}^2,\dots ,S{V}^L]$, 然后将其归一化为单位l2范数，形成用于情绪度量学习的情绪向量(sentiment vector, SV)。

Multi-Task Framework

在标准训练过程中，传统的分类约束（如softmax损失）以最大化正确分类的概率被优化, 给定训练集$\{(x^{(i)},y^{(i)}){\}}_{i=1}^N$,
令$\{h_j^{(i)}|j=1,2,\dots ,C\}$表示$x^{(i)}$最后一个完全连接层中单元$j$的激活值(activation values), 通过最小化softmax loss对最后一层进行微调：$$E_{cls}=-\frac{1}{N}[\sum _{i=1}^N\sum _{j=1}^C\text{1}(y^{(i)}=j\ln p_j^{(i)})]$$式中$\text{1}(\delta )$在$\delta$为真时取1，否则取0。
$p_j^{(i)}$表示$x^{(i)}$标签为$j$的概率，$p_j^{(i)}=\frac{\exp h_j^{(i)}}{{\sum }_{k=1}^C\exp h_k^{(i)}}$, 该softmax的损失可以看作是所有训练图像$\{x^{(i)}\}$上的负对数似然的总和，这将平均惩罚每个类的分类错误，从而忽略类内方差。
给定情感三元组和图像标签作为输入，显式地训练深度模型来优化分类和相似性约束。损失函数是是这两种损失的加权组合: $$E=(1-\omega )E_{cls}+\omega E_{sml}$$

3、Experiment

Dataset

在四个数据集Flickr and Instagram (FI)、IAPSa,、ArtPhoto
和Abstract Paintings上进行实验。

• FI是通过查询Mikels的八种情绪作为关键词从社交网站收集的, 共有23,308张图片
• 国际情感图片系统（IAPS）是一个广泛应用于视觉情感理解研究的常见刺激数据集，IAPSa从中选择了395张带有相同八种情感类别注释的图片
• ArtPhoto包括照片共享网站上的806张艺术照片
• Abstract Paintings包含228幅由颜色和纹理组成的抽象画

Implementation Details

本文基于GoogleNet Inception构建框架，该框架在ImageNet上实现了大规模图像分类的最先进性能。首先使用在大规模数据集上训练的权重初始化网络，然后在FI数据集上进行微调。使用128个批次，通过随机梯度下降（SGD）在整个网络中对所有层进行微调，确保每个情感至少包含8幅图像。实验均在两个NVIDIA GTX 1080 GPU上进行(CPU内存为32 GB)。

Evaluation on the FI dataset

首先在当前最大的FI数据集上，对不同的算法进行评估

Constraints and Sampling Methods

下表展示了FI数据集上分类和检索任务的性能。'∗’, ‘•’, ‘$\diamond$’表示使用不同的抽样方法（即随机抽样、硬抽样、半硬抽样）。使用不同的嵌入来表示情感，即完全连接层（FC）、情感向量（SV）

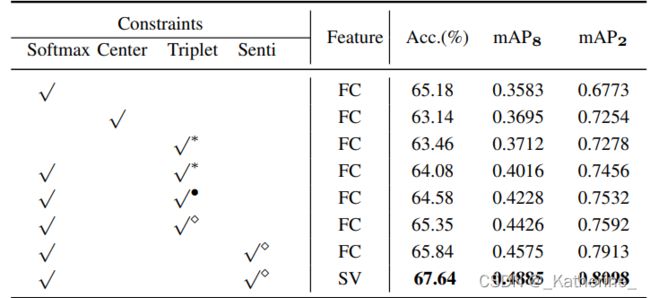
• 根据实验，本文选择了实验结果较好的semi-hard抽样方式，即考虑所有正图像，并在小批量中随机选择负图像，此种方法收敛较快且比较稳定。
• 实验同样表明，采用本文提出的**联合训练分类损失(softmax)和情感相似度损失(senti)**的方式，能够取得更好的结果。
• 更进一步，使用本文提出的情感向量(SV)能够得到比直接使用全连接层作为embedding更好的效果，证明了本文提出的情绪约束(sentiment constraint)能够捕捉情绪之间的关系。

为了更加直观地体现SV的效果，在FI的测试集上使用t-SNE对不同方式的embedding进行可视化。
如下图所示，不同的颜色代表不同的情感标签，(a)(b)表示使用FC层作为嵌入的特征空间，而©表示在框架中使用情感向量SV的特征空间。

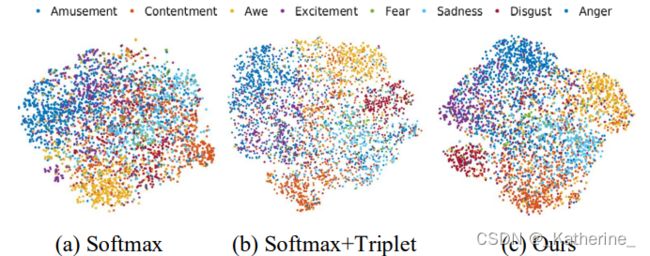
根据可视化结果，可以看出使用本文提出的方式能够更好地区分不同类别的图像。情感约束的特征始终比传统softmax损失的特征分离得更好，而本文的方法进一步扩大了类间方差，这得益于将情感关系纳入特征学习过程。

Affective Image Retrieval & Classification

作者比较了以往算法与本文提出的算法在FI数据集上的分类和检索性能，下表展示了学习情绪表征的不同baseline，包括传统方法和基于CNN的方法。此处“S+T”表示使用softmax和triple loss联合训练模型。（ImageNet是唯一没有微调的模型，其他模型已在FI数据集上进行了微调）
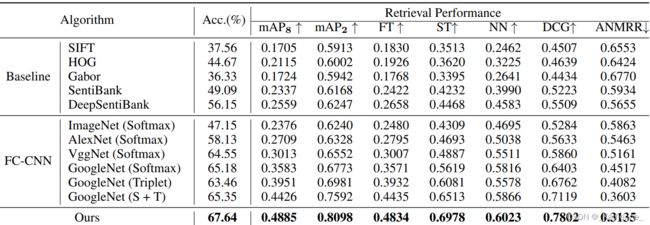与baseline进行比较，结果表明本文提出的方法在各项任务上都取得了更好的效果。

作者在文章中给出了检索任务的几个例子：上图是使用本文提出方法的检索结果实例，给定查询图像（第一列），显示前3名检索结果和相应的欧几里德距离。此外，最后一行展示了检索错误的例子（红色边框的图片）。

Results on Other Datasets

借助迁移学习，在另外三个较小的数据集上重复上述实验，并与其他几种最先进的方法进行了比较
实验结果表明，在这三个数据集中，本文提出的框架均达到了最优结果，这也体现出了对小规模数据集的泛化能力。

4、Concusion

• 在这项工作中，作者通过深度度量学习整合情绪的层次关系，并提出一个多任务框架，以端到端的方式联合优化分类损失和情绪相似度损失。
• 构建情感约束来利用情感关系，并进一步提出了基于Gram矩阵的情感向量用于情感图像之间的距离比较。
• 大量实验表明，在四种流行的情感数据集上，本文的算法在情感图像分类和检索任务方面都以往方法。