Deep Cosine Metric Learning for Person Re-Identification

论文地址： https://arxiv.org/abs/1812.00442v1
代码地址：https://github.com/nwojke/cosine_metric_learning
代码分析：
deep sort多目标跟踪模型外观特征模型

Abstract

Metric learning aims to construct an embedding where two extracted features corresponding to the same identity are likely to be closer than features from different identities. This paper presents a method for learning such a feature space where the cosine similarity is effectively optimized through a simple re-parametrization of the conventional softmax classification regime. At test time, the final classification layer can be stripped from the network to facilitate nearest neighbor queries on unseen individuals using the cosine similarity metric. This approach presents a simple alternative to direct metric learning objectives such as siamese networks that have required sophisticated pair or triplet sampling strategies in the past. The method is evaluated on two large-scale pedestrian re-identification datasets where competitive results are achieved overall. In particular, we achieve better generalization on the test set compared to a network trained with triplet loss.
度量学习的目的是构建一个嵌入，其中两个提取的特征对应于同一身份可能比来自不同身份的特征更接近。本文提出了一种学习这种特征空间的方法。空间的方法，其中余弦相似度被有效地优化了通过对传统的softmax分类系统进行简单的重新参数化，有效地优化了这种特征空间。softmax分类系统的简单再参数化，有效地优化了余弦相似性。在测试时，最后的分类层可以从网络中剥离出来，以便于使用余弦相似度指标对未见过的个体进行近邻查询。余弦相似性指标。这种方法为直接的度量学习目标提供了一个简单的替代方案，如连体网络的简单替代方案，因为过去需要复杂的配对或三联体采样策略。该方法在两个大规模的行人重新识别数据集上进行了评估。其中，总体上取得了有竞争力的结果。特别是，与用三倍体损失训练的网络相比，我们在测试集上取得了更好的泛化效果。

1. Introduction

Person re-identification is a common task in video surveillance where a given query image is used to search a large gallery of images potentially containing the same person. As gallery images are usually taken from different cameras at different points in time, the system must deal with pose variations, different lighting conditions, and changing background. Furthermore, direct identity classification is prohibited in this scenario because individuals in the gallery collected at test time are not contained in the training set. Instead, the re-identification problem is usually addressed within a metric learning framework. Here the goal is to learn a feature representation – from a set of separate training identities – suitable for performing nearest neighbor queries on images and identities provided at test time. Ideally, the learnt feature representation should be invariant to the aforementioned nuisance conditions while at the same time follow a predefined metric where feature similarity corresponds to person identity.
人员重新识别是视频监控中的一项常见任务，即用给定的查询图像来搜索可能包含同一人的大量图像库。由于图库中的图像通常是在不同的时间点由不同的摄像机拍摄的，系统必须处理姿势变化、不同的照明条件和变化的背景。此外，在这种情况下，直接的身份分类是被禁止的，因为在测试时间收集的画廊中的个人不包含在训练集中。相反，重新识别的问题通常在一个度量学习框架内解决。这里的目标是学习一个特征表示从一组单独的训练身份中学习适合于对测试时提供的图像和身份进行近邻查询。理想情况下，学习到的特征表示应该不受上述干扰条件的影响，同时遵循一个预定的度量，其中特征相似度与人的身份相对应。
Due to the annotation effort that is necessary to set up a person re-identification dataset, until recently only a limited amount of labeled images were available. This has changed with publication of the Market 1501 [36] and MARS [35] datasets. MARS contains over one million images that have been annotated in a semi-supervised fashion. The data has been generated using a multi-target tracker that extracts short, reliable trajectory fragments that were subsequently annotated to consistent object trajectories. This annotation procedure not only leads to larger amount of data, but also puts the dataset closer to real-world applications where people are more likely extracted by application of a person detector rather than manual cropping.
由于建立一个人的重新识别数据集所需的注释工作，直到最近，只有有限的标记图像可用。随着Market 1501[36]和MARS[35]数据集的发布，这种情况有所改变。MARS包含超过一百万张以半监督方式标注的图像。这些数据是通过一个多目标跟踪器产生的，该跟踪器提取了简短、可靠的轨迹片段，随后被注释为一致的物体轨迹。这种注释程序不仅导致了更大的数据量，而且使数据集更接近于现实世界的应用，在那里人们更有可能通过应用人的检测器而不是手工裁剪来提取。

Figure 1: The proposed classifier successfully learns a metric representation space that is robust to articulation, lighting, and background variation. For each query image the five most similar and dissimilar images are shown. 图1：提议的分类器成功地学习了一个对衔接、照明和背景变化具有鲁棒性的度量表示空间。对于每张查询图像 显示了五张最相似和最不相似的图像。

Much like in other vision tasks, deep learning has become the predominant paradigm to person re-identification since the advent of larger datasets. Yet, the problem remains challenging and far from solved. In particular, there is an ongoing discourse over the performance of direct metric learning objectives compared to approaching the training procedure indirectly in a classification framework. Whereas metric learning objectives encode the similarity metric directly into the training objective, classification-based methods train a classifier on the set of identities in the training set and then use the underlying feature representation of the network to perform nearest neighbor queries at test time. On the one hand, in the past direct metric learning objectives have suffered from undesirable properties that can hinder optimization, such as non-smoothness or missing contextual information about the neighborhood structure [19]. On the other hand, these problems have been approached with success in more recent publications [18, 8]. Nevertheless, with similarity defined solely based on class membership, it remains arguable if direct metric learning has a clear advantage over training in a classification regime. In this setting, metric learning is often reduced to minimizing the distance between samples of the same class and forcing a margin between samples of different classes [3, 8]. A classifier that is set up with care might decrease intra-class variance and increase inter-class variance in a similar way to direct metric learning objectives.
与其他视觉任务一样，自从有了更大的数据集，深度学习已经成为人物重新识别的主要范式。然而，这个问题仍然具有挑战性，远远没有得到解决。特别是，与在分类框架中间接处理训练程序相比，直接的度量学习目标的性能有一个持续的讨论。度量学习目标直接将相似度量编码到训练目标中，而基于分类的方法在训练集的身份集合上训练分类器，然后在测试时使用网络的底层特征表示来进行近邻查询。一方面，在过去，直接的度量学习目标有一些不理想的特性，会阻碍优化，比如非平滑性或缺少关于邻域结构的上下文信息[19]。另一方面，这些问题在最近的出版物中得到了成功的解决[18, 8]。然而，由于相似性仅仅是基于类的成员资格来定义的，直接的度量学习是否比分类制度的训练有明显的优势，这一点仍然值得商榷。在这种情况下，度量学习通常被简化为最小化同一类别的样本之间的距离，并在不同类别的样本之间强加一个余量[3, 8]。一个精心设置的分类器可能会以类似于直接公因子学习目标的方式减少类内方差，增加类间方差。
Inspired by this discussion, the main contribution of this paper is the unification of metric learning and classification. More specifically, we present a careful but simple re-parametrization of the softmax classifier that encodes the metric learning objective directly into the classification task. Finally, we demonstrate how our proposed cosine softmax training extends the effectiveness of the learnt embedding to unseen identities at test time within the context of person re-identification. Source code of this method is provided in a GitHub repository¹.
受这一讨论的启发，本文的主要贡献是统一了度量学习和分类。更具体地说，我们提出了一个仔细但简单的softmax分类器的重新参数化，将度量学习目标直接编码到分类任务中。最后，我们展示了我们提出的余弦软键训练是如何将学习到的嵌入的有效性扩展到人的重新识别背景下的测试时间的未见过的身份。该方法的源代码在GitHub仓库中提供¹。
https://github.com/nwojke/cosine_metric_learning

2. Related Work

Metric Learning Convolutional neural networks (CNNs) have shown impressive performance on large scale computer vision problems and the representation space underlying these models can be successfully transferred to tasks that are different from the original training objective [5, 22]. Therefore, in classification applications with few training examples a task-specific classifier is often trained on top of a general purpose feature representation that was learned beforehand on ImageNet [11] or MS COCO [16]. There is no guarantee that the representation of a network which has been trained with a softmax classifier can directly be used in an image retrieval task such as person re-identification, because the representation does not necessarily follow a certain (known) metric to be used for nearest-neighbor queries. Nevertheless, several successful applications in face verification and person re-identification exist [24, 31, 37]. In this case, a softmax classifier is trained to discriminate the identities in the training set. When training is finished, the classifier is stripped of the network and distance queries are made using cosine similarity or Euclidean distance on the final layer of the network. If, however, the feature representation cannot be used directly, an alternative is to find a metric subspace in a post processing step [10, 15].
机器学习 卷积神经网络（CNN）在大规模的计算机视觉问题上表现出令人印象深刻的性能，而且这些模型所依据的表示空间可以成功地转移到与原始训练目标不同的任务上[5, 22]。因此，在有少量训练实例的分类应用中，特定任务的分类器通常是在事先在ImageNet[11]或MS COCO[16]上学习的通用特征表示之上训练的。不能保证用softmax分类器训练的网络表征能直接用于图像检索任务，如人的重新识别，因为该表征不一定遵循某种（已知的）尺度，以用于最近邻的查询。然而，在人脸验证和人的重新识别中存在一些成功的应用[24, 31, 37]。在这种情况下，一个softmax分类器被训练来辨别训练集中的身份。训练结束后，分类器被从网络中剥离，并在网络的最后一层使用余弦相似度或欧氏距离进行距离查询。然而，如果不能直接使用特征表示，另一种方法是在后处理步骤中找到一个度量子空间[10, 15]。
Deep metric learning approaches encode notion of similarity directly into the training objective. The most prominent formulations are siamese networks with contrastive [3] and triplet [28] loss. The contrastive loss minimizes the distance between samples of the same class and forces a margin between samples of different classes. Effectively, this loss pushes all samples of the same class towards a single point in representation space and penalizes overlap between different classes. The triplet loss relaxes the contrastive formulation to allow samples to move more freely as long as the margin is kept. Given an anchor point, a point of the same class, and a point of a different class, the triplet loss forces the distance to the point of the same class to be smaller than the distance to the point of the different class plus a margin.
深度度量学习方法将相似性的概念直接编码到训练目标中。最突出的表述是具有对比性[ 3 ] 和三重性[28]损失的连体网络。对比性损失使同一类别的样本之间的距离最小化，并迫使不同类别的样本之间有一个差值。有效地，这种损失将同一类别的所有样本推向表示空间的一个点，并惩罚不同类别之间的重叠。三重损失放宽了对比性的表述，允许样本更自由地移动，只要保持余量。给定一个锚点，一个相同类别的点和一个不同类别的点，三重损失迫使到相同类别的点的距离小于到不同类别的点的距离，再加上一个余量。
Both the contrastive and triplet losses have been applied successfully to metric learning problems (e.g., [21, 26, 8]), but the success has long been dependent on an intelligent pair/triplet sampling strategy. Many of the possible choices of pairs and triplets that one can generate from a given dataset contain little information about the relevant structures by which identities can be discriminated. If the wrong amount of hard to distinguish pairs/triplets are incorporated into each batch, the optimizer either fails to learn anything meaningful or does not converge at all. Development of an effective sampling strategy can be a complex and time consuming task, thus limiting the practical applicability of siamese networks.
对比性损失和三联体损失都已经成功地应用于度量学习问题（例如，[21, 26, 8]），但长期以来，其成功取决于智能的对/三联体采样策略。从一个给定的数据集中可以产生的许多可能的对和三联体的选择，几乎不包含可以区分身份的相关结构的信息。如果在每一批中加入错误数量的难以区分的对/三联体，那么优化器要么不能学到任何有意义的东西，要么根本就不能收敛。开发有效的抽样策略可能是一项复杂而耗时的任务，因此限制了连体网络的实际适用性。
A second issue related to the contrastive and triplet loss stems from the hard margin that is enforced between samples of different classes. The hard margin leads to a nonsmooth objective function that is harder to optimize, because only few examples are presented to the optimizer at each iteration and there can be strong disagreement between different batches [19]. These problems have been addressed recently. For example, Song et al. [18] formulate a smooth upper bound of the original triplet loss formulation that can be implemented by drawing informative samples from each batch directly on a GPU. A similar formulation of the triplet loss where the hard margin is replaced by a soft margin has shown to perform well on a person re-identification problem [8].
与对比性和三联体损失有关的第二个问题来自于不同类别的样本之间强制执行的硬边距。硬边距导致非平滑目标函数更难优化，因为每次迭代时只有少数例子被提交给优化器，而且不同批次之间可能存在强烈的分歧[19]。这些问题最近已经得到解决。例如，Song等人[18]制定了一个原始三联体损失公式的平滑上界，可以通过在GPU上直接从每批中抽取信息样本来实现。一个类似的三联体损失的表述，其中硬边际被软边际取代，在一个人的重新识别问题上表现良好[8]。
Apart from siamese network formulations, the magnet loss [19] has been formulated as an alternative to overcoming many of the related issues. The loss is formulated as a negative log-likelihood ratio between the correct class and all other classes, but also forces a margin between samples of different classes. By operating on entire class distributions instead of individual pairs or triplets, the magnet loss potentially converges faster and leads to overall better solutions. The center loss [29] has been developed in an attempt to combine classification and metric learning. The formulation utilizes a combination of a softmax classifier with an additional term that forces compact classes by penalizing the distance of samples to their class mean. A scalar hyperparameter balances the two losses. Experiments suggest that this joint formulation of classification and metric learning produces state of the art results.
除了连体网络公式，磁铁损失[19]也被制定为克服许多相关问题的替代方案。该损失被表述为正确类别和所有其他类别之间的负对数似然比，但也迫使不同类别的样本之间有一个差值。通过对整个类的分布进行操作，而不是单个的对或三联体，磁损失可能会更快地收敛，并导致整体更好的解决方案。中心损失[29]已经被开发出来，试图结合分类和度量学习。该公式利用softmax分类器与一个附加项的组合，该附加项通过惩罚样本与它们的类平均值的距离来强制压缩类。一个标量超参数平衡了这两种损失。实验表明，这种分类和度量学习的联合配方产生了最先进的结果。
Person Re-Identification With the availability of larger datasets, person re-identification has become an application domain of deep metric learning and several CNN architectures have been designed specifically for this task. Most of them focus on mid-level features and try to deal with pose variations and viewpoint changes explicitly by introducing special units into the architecture. For example, Li et al. [13] propose a CNN with a special patch matching layer that captures the displacement between mid-level features. Ahmed et al. [1] capture feature displacements similarly by application of special convolutions that compute the difference between neighborhoods in the feature map of two input images. The gating functions in the network of Varior et al. [26] compare features along a horizontal stripe and output a gating mask to indicate how much emphasis should be paid to the local patterns. Finally, in [27] a recurrent siamese neural network architecture is proposed that processes images in rows. The idea behind the recurrent architecture is to increase contextual information through sequential processing.
Person Re-Identification 随着大型数据集的出现，人的重新识别已经成为深度度量学习的一个应用领域，一些CNN架构已经被专门设计用于这项任务。它们中的大多数都集中在中层特征上，并试图通过在架构中引入特殊单元来明确处理姿势变化和视角变化。例如，Li等人[13]提出了一个具有特殊补丁匹配层的CNN，该层可以捕捉到中层特征之间的位移。Ahmed等人[1]通过应用特殊的卷积，计算两幅输入图像的特征图中邻域之间的差异，以类似的方式捕捉特征位移。Varior等人[26]的网络中的门控功能沿水平条纹比较特征，并输出门控掩码，以表明对局部模式应给予多大的重视。最后，在[27]中提出了一个递归的连体神经网络架构，它以行为单位处理图像。递归结构背后的想法是通过顺序处理来增加背景信息。
More recent work on person re-identification suggests that baseline CNN architectures can compete with their specialized counter parts. In particular, the current best performing method on the MARS [35] is a conventional residual network [8]. Application of baseline CNN architectures can be beneficial if pre-trained models are available for finetuning to the person re-identification task. Influence of pretraining on overall performance is studied in [35]. They report between 9.5% and 10.2% recognition rate is due to pre-training on ImageNet [11].
最近关于人的重新识别的工作表明，基线CNN架构可以与它们的专门对应部分竞争。特别是，目前在MARS[35]上表现最好的方法是一个传统的剩余网络[8]。如果预先训练好的模型可以用来对人的重新识别任务进行微调，那么基线CNN架构的应用就会有好处。预训练对整体性能的影响在[35]中被研究。他们报告说9.5%到10.2%的识别率是由于ImageNet上的预训练造成的[11]。

3. Standard Softmax Classifier

Given a dataset $D=\{(x_i,y_i){\}}_{i=1}^N$ of N training images $x_i\in {\mathbb{R}}^D$ and associated class labels $y_i\in \{1,...,C\},$ the standard approach to classification in the deep learning setting is to process input images by a CNN and place a softmax classifier on top of the network to obtain probability scores for each of the C classes. The softmax classifier chooses the class with maximum probability according to a parametric function
给定数据集$D=\{(x_i,y_i){\}}_{i=1}^N$, N个训练图像$x_i\in {\mathbb{R}}^D$和相关的类标签$y_i\in \{1,...,C\},$，在深度学习设置中，标准的分类方法是通过CNN处理输入图像，并将softmax分类器放置在网络的顶部，以获得每个C类的概率得分。softmax分类器根据参数函数选择概率最大的类

$$p(y=k|r)=\frac{exp(w_k^{T}r+b_k)}{{\sum }_{n=1}^{C}exp(w_k^{T}r+b_k)}$$
where $r=f(x),r\in {\mathbb{R}}^d$ is the underlying feature representation of a paprametrized encoder network that is trained jointly with the classifier. For the special case of C = 2 classes this formulation is equivalent to logistic regression. Further, the specific choice perspective on the classification problem. If the class-conditional densities are Gaussian
其中 $r=f(x),r\in {\mathbb{R}}^d$ 是与分类器联合训练的参数化编码器网络的底层特征表示。对于C =2类的特殊情况，这个公式等价于逻辑回归。进一步，从具体的角度选择分类问题。如果类条件密度是高斯的

$$p(r|y=k)=\frac{1}{\sqrt{|2\pi \sum |}}exp(-\frac{1}{2}(r-u_k{)}^T\sum ^{-}1(r-u_k))$$
with shared covariance $\sum$, then the posterior class probability can be computed by Bayes’ rule

共有协方差$\sum$，则后验类概率可由贝叶斯规则计算

$$p(y=k|r)=\frac{p(r|y=k)p(y=k)}{{\sum }_{n=1}^{C}p(r|y=n)p(y=n)}$$
$$=\frac{exp(w_n^{T}r+b_n)}{{\sum }_{n=1}^{C}exp(w_n^{T}r+b_n)}$$

with $w_k={\sum }^{-1}{u}_k$ and $b_k=-\frac{1}{2}{u}_k^T{\sum }^{-1}{u}_k+logp(y_i=k)$[2]. However, the softmax classifier is trained in a discriminative regime. Instead of determining the parameters of the class-conditional densities and prior class probabilities, the parameters $\{w_1,b_1,....,w_C,b_C\}$ of the conditional class probabilities are obtained directly by minimizatioin of a classification loss. Let ${\mathbb{L}}_{y=k}$ denote the indicator function that evaluates to 1 if y is equal to k and 0 otherwise. Then, the corresponding loss

$w_k={\sum }^{-1}{u}_k$ 和 $b_k=-\frac{1}{2}{u}_k^T{\sum }^{-1}{u}_k+logp(y_i=k)$[2]。然而，softmax分类器是在一种判别机制中训练的。不是确定类条件密度和先验类概率的参数，而是参数$\{w_1,b_1,....,w_C,b_C\}$的条件类概率直接通过最小化分类损失得到。让${\mathbb{L}}_{y=k}$表示指示函数，如果y=k，则值为1，否则值为O。然后是相应的损失

$$\mathcal{L}(D)=-\sum _{i=1}^N\sum _{k=1}^C\mathbb{L}{y}_{i}k\bullet logp(y_i=k|r_i)$$
minimizes the cross-entropy between the true label distribution$p(y=k)={\mathcal{L}}_{y=k}$ and estimated probabilities of the softmax classifier $p(y=k|r)$. By minimizing the crossentropy loss, parameters are chosen such that the estimated probability is close to 1 for the correct class and close to 0 for all other classes.

最小化真标签分布 $p(y=k)={\mathcal{L}}_{y=k}$ 和softmax分类器的估计概率p(y = kr)之间的交叉熵。通过最小化互熵损失，参数的选择使正确类的估计概率接近1，而其他所有类的估计概率接近0。

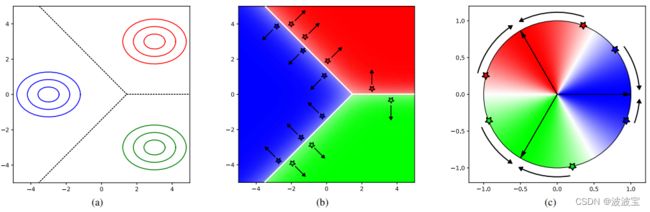
Figure 2a shows three Gaussian densities $p(r|y)$ together with the corresponding decision boundary. The posterior class probabilities of this scenario are shown in Figure 2b together with a set of hypothesized training examples. Whereas the Gaussian densities peak around a class mean, the posterior calss probability is a function of the distance to the decision boundary. When the feature encoder is trained with the classifier jointly by minimization of the cross-entropy loss, the parameters of the encoder network are adapted to push samples away from the decision boundary as far as possible, but not necessarily towards the class mean that has been taken to motivate the specific functional form. This behavior is problematic for metric learning because similarity in terms of class membership is encoded in the orientation of the decision boundary rather than in the feature representation itself.

图2a显示了三个高斯密度 $p(r|y)$以及相应的决策边界。此场景的后验类概率如图2b所示，并给出了一组假设的训练示例。而高斯密度峰值在类均值附近，后验类概率是到决策边界的距离的函数。当编码器的功能是训练的分类器由最小化叉损失,编码器的参数网络适应推动样品尽量远离边界的决定,但不一定对该类意味着被激励的具体函数形式。这种行为对于度量学习来说是有问题的，因为在类成员方面的相似性是在决策边界的方向中编码的，而不是在特征表示本身中。

Figure 2: Plot (a) shows three Gaussian class-conditional densities (iso-contours) and the corresponding decision boundary (dashed lines). Plot (b) shows the conditional class probabilities (color coded) and a set of hypothesized training examples. The softmax classifier models the posterior class probabilities directly, without construction of Gaussian densities. By training with the cross-entropy loss, samples are pushed away from the decision boundary, but not necessarily towards a class mean. Plot (c) illustrates the posterior class probabilities (color coded) and decision boundary (white line) of the cosine softmax classifier for three classes. During training, all samples are pushed away from the decision boundary towards their parametrized class mean direction (indicated by an arrow). 图2:图(a)显示了三个高斯类条件密度(等高线)和相应的决策边界(虚线)。图(b)显示了条件类概率(颜色编码)和一组假设的训练示例。softmax分类器直接建模后验类概率，无需构造高斯密度。通过训练交叉熵损失，样本被推离决策边界，但不一定是向类均值。图(c)显示了三个类的余弦软max分类器的后验类概率(彩色编码)和决策边界(白线)。在训练过程中，将所有样本从决策边界推向其参数化的类均值方向(用箭头表示)

4. Cosine Softmax Classifier

With few adaptations the standard softmax classifier can ben modified to produce compact clusters in representation space. First, ${\mathcal{L}}_2$ normalization must be applied to the fimal layer of the encoder network to ensure the representation is unit length $\Vert f_{\partial }(x){\Vert }_2=1,{\forall }_x\in {\mathbb{E}}^D$. Second, the weights must be normalized to unit-mength as well, i.e., $w_k=w_k/\Vert w_k{\Vert }_2,\forall k=1,...,C$. Then, the cosine softmax classifier can be stated by

只需少量修改，标准softmax分类器就可以在表示空间中产生紧凑的簇。首先，编码器网络的最后一层必须对${\mathcal{L}}_2$归一化，以确保表示为度量归一化 $\Vert f_{\partial }(x){\Vert }_2=1,{\forall }_x\in {\mathbb{E}}^D$。其次，权重也必须归一化到单位长度，即$w_k=w_k/\Vert w_k{\Vert }_2,\forall k=1,...,C$。 那么，cos softmax分类器可以表示为

$$p(y_i=k|r_i)=\frac{exp(k\cdot w_n^T{r}_i)}{{\sum }_{n=1}^{C}exp(k\cdot w_n^T)},$$
where $k$ is a free scaling parameter. This parametrization has $C-1$ fewer parameters parameters compared to the standard formulation (1) because the bias terms $b_k$ have been removed$\{k,w_1,....,w_C\}$. Otherwise, the funcational form resembles strong similarity to the standard parametrization and implementaion is straight-forward. In particular, decoupling the length of the weight vector $k$ from its direction has been proposed before[20] as a way to accelerate convergence of stochastic gradient descent. Training itself can be carried out using the cross-entropy loss as usual since the cosine softmax classifier is merely a change of parameterization compared to the standard formulation.
其中 $k$ 为自由缩放参数。与标准公式(1)相比，此参数化具有少 $C-1$ 的参数参数，因为偏差项 $b_k$ 已被删除$\{k,w_1,....,w_C\}$。否则，函数形式类似于标准参数化和实现是直接的。特别地，在[20]之前已经提出将权向量k的长度与其方向解耦，以加速随机梯度下降法的收敛。训练本身可以像往常一样使用交叉熵损失进行，因为cossoftmax分类器与标准公式相比只是参数化的变化。

The functional modeling of log-probabilities by $k\cdot w_K^{T}r$ can be motivated from a generative perspective as well. If the class-conditioinal likelihoods follow a von Mises-Fisher(vMF) distribution

由 $k\cdot w_K^{T}r$ 建立的对数概率函数模型也可以从生成式的角度出发。如果类条件似然服从von MisesFisher(vMF)分布
$$p(r|y=k)=c_d(k)exp(k\cdot w_k^{T}r),$$
with shared concentration parameter $k$ and normalizer $c_d(k)$, then Equation 6 is the posterior class probability under an equal prior assumption $p(y=k)=p(y=l),\forall k,l\in \{1,....,C\}$. The vMF distribution is an isotropic probability distribution on the d-1 dimensional sphere in ${\mathbb{R}}^d$ that peaks mean direction $w_k$ and decays as the cosine similarity decreases.
有共享浓度参数$k$和归一化器$c_d(k)$，则式6为等先验假设$p(y=k)=p(y=l),\forall k,l\in \{1,....,C\}$ . vMF分布是d-1维球上${\mathbb{R}}^d$ 上的各向同性概率分布，在$w_k$ 方向上峰值，随着余弦相似度的降低而衰减。

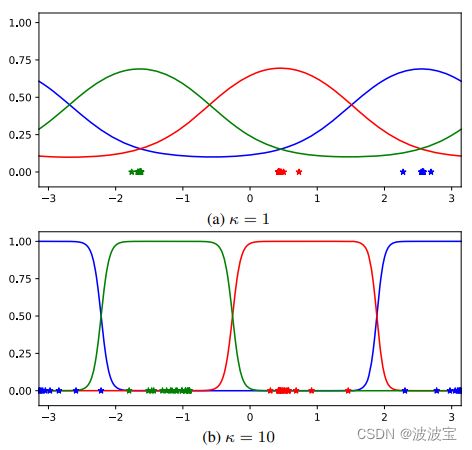
To understand why this parametrization enforces a cosine similarity on the representation space, observe that the log-probabilities are directly proportional to the cosine similarity between training examples and a parametrized class mean direction. By minimizing the cross-entropy loss, examples are pushed away from the decision boundary towards their parametrized mean as illustrated in Figure 2c. In onsequence, parameter vector $w_k$ becomes a surrogate for all samples in cases k. The scaling parameter κ controls the shape of the conditional class probabilities as illustrated in Figure 3. A low value corresponds to smoother functions with wider support. A high κ value leads to conditional class probabilities that are box-like shaped around the decision boundary. This places a larger penalty on misclassified examples, but at the same time leaves more room for samples to move freely in the region of representation space that is occupied by its corresponding class. In this regard, the scale takes on a similar role to margin parameters in direct metric learning objectives. When the scale is left as a free parameter, the optimizer gradually increases its value as the overlap between classes reduces. A margin between samples of different classes can be enforced by regularizing the scale with weight decay.
为了理解为什么这个参数化在表示空间上强制一个余弦相似度，观察对数概率直接与训练示例和参数化的类平均方向之间的余弦相似度成比例。通过最小化交叉熵损失，示例被从决策边界推向其参数化平均值，如图2c所示。因此，参数向量 $w_k$ 成为情况k中所有样本的代理。缩放参数k控制条件类概率的形状，如图3所示。低值对应的是支持范围更广的平滑函数。高K值会导致在决策边界周围形成框状的条件类概率。这对错误分类的例子施加了更大的惩罚，但同时也为样本在其对应类所占据的表示空间区域内的自由移动留下了更多的空间。在这方面，规模采取了类似的作用，边际参数在直接度量学习目标。当比例作为自由参数保留时，随着类之间重叠的减少，优化器逐渐增加它的值。不同类别的样本之间的差值可以通过权重衰减来规范尺度。

Figure 3: Illustration of the free scaling parameter κ in a one dimensional problem with three classes. The conditional class probabilities are shown as colored functions. Optimized sample locations are visualized as stars at y = 0. A low κ value (a) leads to smoother functions with wider support, such that samples are pushed into tight clusters. The shape becomes box-like for high values (b), allowing samples to move more freely within a region that is occupied by the class. 图3：自由缩放参数κ在一个有三类的一维问题中的说明。维问题中的自由比例参数κ的说明，有三个类别。条件类概率显示为彩色函数。优化后的样本位置在y=0处显示为星星。低κ值（a）会导致具有更宽支持度的平滑函数，从而使样本被推入紧密的集群中。对于高值（b），形状变得像盒子，允许样本在被类所占据的区域内更自由地移动。

5. Evaluation

The first part of the evaluation compares both the training behavior and validation error between our loss formulation and common metric learning losses using a network trained from scratch. In the second part, overall system performance is established against existing re-identification systems on the same datasets.

评估的第一部分比较了我们的损失公式和使用从零开始训练的网络的普通度量学习损失之间的训练行为和验证误差。在第二部分中，针对相同数据集上的现有重新识别系统建立总体系统性能。

5.1. Network Architecture

The network architecture used in our experiments is relatively shallow to allow for fast training and inference, e.g., for application in the related task of appearance based object tracking [30]. The architecture is summarized in Table 1. Input images are rescaled to 128 × 64 and presented to the network in RGB color space. A series of convolutional layers reduces the size of the feature map to 16 × 8 before a global feature vector of length 128 is extracted by layer Dense 10. The final 2 normalization projects features onto the unit hypersphere for application of the cosine softmax classifier. The network contains several residual blocks that follow the pre-activation layout proposed by He et al. [7]. The design follows the ideas of wide residual networks [33]: All convolutions are of size 3 × 3 and max pooling is replaced by convolutions of stride 2. When the spatial resolution of the feature map is reduced, then the number of channels is increased accordingly to avoid a bottleneck. Dropout and batch normalization are used as means of regularization. Exponential linear units [4] are used as activation function in all layers.

我们实验中使用的网络架构比较浅，可以进行快速的训练和推理，例如应用在基于外观的对象跟踪[30]的相关任务中。表1总结了该体系结构。输入图像缩放到128 x 64，在RGB颜色空间中呈现给网络。一系列卷积层将feature map的大小减少到16 x 8，然后通过layer Dense 10提取一个长度为128的全局特征向量。最后2个归一化方案将特征投影到单位超球上，用于cossoftmax分类器的应用。该网络包含几个残块，它们遵循He等人[7]提出的预激活布局。设计遵循宽剩余网络[33]的思想:所有卷积的大小为3 x 3，最大池化被stride 2的卷积取代。当特征图的空间分辨率降低时，相应增加通道数，以避免出现瓶颈。采用Dropout和batch归一化作为正则化手段。各层均采用指数线性单位[4]作为激活函数。

Note that with in total 15 layers (including two convolutional layers in each residual block) the network is relatively shallow when compared to the current trend of ever deeper architectures [7]. This decision was made for the following two reasons. First, the network architecture has been designed for the application of both person re-identification and online people tracking [30], where the latter requires fast computation of appearance features. In total, the network has 2,800,864 parameters and one forward pass of 32 bounding boxes takes approximately 30 ms on an Nvidia GeForce GTX 1050 mobile GPU. Thus, this network is well suited for online tracking even on low-cost hardware. Second, architectures that have been designed for person reidentification specifically [13, 1] put special emphasis on mid-level features. Therefore, the dense layer is added at a point where the feature map still provides enough spatial resolution.

请注意，总共有15层(包括两个卷积层在每个残差块)，与目前的更深层次架构[7]相比，网络是相对较浅的。作出这一决定有两个原因。首先，设计了既适用于人的再识别，又适用于在线跟踪[30]的网络架构，后者需要快速计算外观特征。该网络总共有2,800,864个参数，在Nvidia GeForce GTX 1050移动GPU上，32个包围盒的一次向前传递大约需要30毫秒。因此，即使在低成本的硬件上，这个网络也非常适合在线跟踪。其次，专门为人员再识别设计的体系结构[13,1]特别强调了中层特征。因此，致密层被添加在feature map仍然提供足够空间分辨率的点上。

5.2. Datasets and Evaluation Protocols

Evaluation is carried out on the Market 1501 [36] and MARS [35]. Market 1501 contains 1,501 identities and roughly 30,000 images taken from six cameras. MARS is an extension of Market 1501 that contains 1,261 identities and over 1,100,000 images. The data has been generated using a multi-target tracker that generates tracklets, i.e. short-term track fragments, which have then been manually annotated to consistent identities. Both datasets contain considerate bounding box misalignment and labeling inaccuracies. For all experiments a single-shot, cross-view evaluation protocol is adopted, i.e. a single query image from one camera is matched against a gallery of images taken from different cameras. The gallery image ranking is established using cosine similarity or Euclidean distance, if appropriate. Training and test data splits are provided by the authors. Additionally, 10% of the training data is split for hyperparameter tuning and early stopping. On both datasets cumulative matching characteristics (CMC) at rank 1 and 5 as well as mean average precision (mAP) are reported. The scores are computed with evaluation software provided by the corresponding dataset authors.

对Market 1501[36]和MARS[35]进行评价。1501市场包含1501个身份和大约3万张来自6个摄像头的图像。MARS是1501市场的扩展，包含1,261个身份和超过1,100,000张图像。数据已经使用多目标跟踪器生成轨迹，即短期轨迹碎片，然后手动注释到一致的身份。这两个数据集都包含考虑周到的边界框不对齐和标签不准确。所有实验均采用单镜头、交叉视图评估协议，即从一个摄像头获取的单个查询图像与从不同摄像头获取的图像库进行匹配。图库图像排序是使用余弦相似度或欧氏距离，如果合适。训练和测试数据的分割由作者提供。此外，10%的训练数据被分割用于超参数调优和早期停止。在这两个数据集上，我们报告了1级和5级的累积匹配特征(CMC)和平均平均精度(mAP)。分数由数据集作者提供的评价软件计算。

5.3. Baseline Methods

In order to assess the performance of the joint classification and metric learning framework on overall performance, the network architecture is repeatedly trained with
two baseline direct metric learning objectives.

为了评估联合分类和度量学习框架在整体性能上的表现，网络架构被重复训练两个基线直接度量学习目标。

Triplet loss The triplet loss [28] is defined over tuples of three examples $r_a,r_p$ and $r_n$ that include a positive pair $y_a=y_p$ and a negative pair $y_a\ne y_p$. For each such triplet the loss demands that the difference of the distance between the negative and positive pair is larger than a predefined margin $m\in R$:

三重态损耗[28]定义在三个例子$r_a,r_p$ 和 $r_n$ 的元组上，其中包括一对正的$y_a=y_p$ 和一对负的$y_a\ne y_p$。对于每一个这样的三元组，损耗要求负极和正极对之间的距离差大于预定义的边界 $m\in R$：

$${\mathcal{L}}_t(r_a,r_p,r_n)=\{\Vert r_a-r_p{\Vert }_2-\Vert r_a-r_n{\Vert }_2+m{\}}_{+},$$
where $\{{\}}_{+}$ denotes the hinge function that evaluates to 0 for negative values and identity otherwise. In this experiment, a soft-margin version of the original triplet loss [8] is used where the hinge is replaced by a soft plus function {x + m}+ = log(1 + exp(x)) to avoid issues with non-smoothness [19]. Further, the triplets are generated directly on GPU as proposed by [8] to avoid potential issues in the sampling strategy. Note that this particular triplet loss formulation has been used to train the current best performing model on the MARS dataset.

其中$\{{\}}_{+}$表示铰链函数，对于负数，其计算值为O，否则为恒等值。在本实验中，我们使用了原始三重损耗[8]的软边缘版本，其中铰链被软加函数[x+ m)+ = log(1 + exp(x))取代，以避免[19]的不平滑问题。此外，根据[8]的建议，三胞胎直接在GPU上生成，以避免采样策略中的潜在问题。请注意，这种特殊的三片损耗公式已被用于训练MARS数据集上当前表现最好的模型。

Magnet loss The magnet loss has been proposed as an alternative to siamese loss formulations that works on entire class distribution rather than individual samples. The loss is a likelihood ratio measure that forces separation in terms of each sample’s distance away from the means of other classes. In its original proposition [19] the loss takes on a multi-modal form. Here, a simpler, unimodal variation of this loss is employed as it better fits the single-shot person re-identification task:

磁体损耗已被提出作为连体损耗公式的替代，该公式适用于整个类分布，而不是单个样本。损失是一种似然比度量，它迫使每个样本与其他类别均值的距离分离。在其原始命题[19]中，损失具有多模态形式。这里，我们采用了这种损失的一个更简单的单峰变化，因为它更适合单次射击的人的重新识别任务:

$${\mathcal{L}}_m(y,r)=\{-log\frac{e^{\frac{1}{2e^2}\Vert r-u_y{\Vert }_2^2-m}}{{\sum }_{k\in C(y)}{e}^{\frac{1}{2e^2}\Vert r-u_y{\Vert }_2^2-m}}{\}}_{+},$$
where $c(y)=\{1,....,C\}\{y\}$,$m$ is again a margin parameter, $u_y$ is the sample mean of class y, and $q^2$ is the variance of all samples away from their class mean. These parameters are computed on GPU for each batch individually.

其中$c(y)=\{1,....,C\}\{y\}$,$m$又是一个边缘参数， $u_y$是y类的样本均值，$q^2$ 是所有样本离其类均值的方差。这些参数是在GPU上为每批单独计算的。

5.4. Results

The results reported in this section have been established by training the network for a fixed number of 100, 000 iterations using Adam [9]. The learning rate was set to 1 × 10−3. As can be seen in Figure 4 all configurations have fully converged at this point. The network was regularized with a weight decay of 1 × 10−8 and dropout inside the residual units with probability 0.4. The margin of the magnet loss has been set to m = 1 and the cosine softmax scale κ was left as a free parameter for the optimizer to tune, but regularized with a weight decay of 1 × 10−1. The batch size was fixed to 128 images. Gallery rankings are established using Euclidean distance in case of magnet and triplet loss, while cosine similarity is used for the softmax classifier. To increase variability in the training set, input images have been randomly flipped, but no random resizing or cropping has been performed.

本节中报告的结果是通过使用Adam[9]对网络进行固定数量的10万次迭代来建立的。学习速率设置为1 × 10-3。如图4所示，此时所有配置都已完全收敛。网络正则化，权值衰减为1 × 10-8，残差单元内的缺失概率为0.4。磁体损失的裕度被设为m = 1，余弦softmax尺度k被留作优化器的自由参数来进行调优，但用1 x 10-1的权重衰减进行了正则化。批处理大小固定为128张图像。在磁体和三重态损失的情况下，使用欧氏距离建立图库排名，而在softmax分类器中使用余弦相似度。为了增加训练集的可变性，对输入图像进行了随机翻转，但没有进行随机调整大小或裁剪。

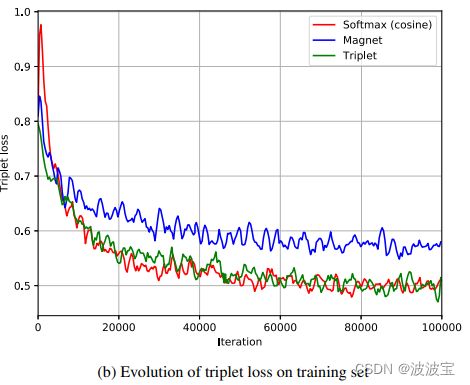
Training Behavior Figure 4a shows the rank 1 matching rate on the validation set of MARS as a function of training iterations. The results obtained on Market 1501 are omitted here since the training behavior is similar. The network trained with cosine softmax classifier achieves overall best performance, followed by the network trained with soft-margin triplet loss. The best validation performance of the softmax network is reached at iteration 49 760 with rank 1 matching rate 84.92%. The best performance of the triplet loss network is reached at iteration 86 329 with rank 1 matching rate 83.23%. The magnet loss network reaches its best performance at iteration 47 677 with rank 1 matching rate 77.34%. Overall, the convergence behavior of the three losses is similar, but the magnet loss falls behind on final model performance. In its original implementation [19] the authors sample batches such that similar classes appear in the same batch. For practical reasons such more informative sample mining has not been implemented. Instead, a fixed number of images per individual was randomly selected for each batch. Potentially, the magnet loss suffers from this less informative sampling strategy more than the other two losses.

图4a显示了MARS验证集的秩1匹配率作为训练迭代的函数。在市场1501上得到的结果在这里省略，因为训练行为是相似的。使用cossoftmax分类器训练的网络总体性能最好，其次是使用软裕量三联损失训练的网络。softmax网络的验证性能在迭代49 760时达到最佳，一级匹配率为84.92%。迭代86 329时三态损耗网络性能最佳，秩1匹配率为83.23%。磁损耗网络在迭代47 677时性能最佳，一级匹配率为77.34%。总的来说，三种损耗的收敛行为相似，但磁体损耗落后于最终模型的性能。在其原始实现[19]中，作者对批处理进行了采样，以便在同一批处理中出现类似的类。由于实际原因，这种信息更丰富的样本挖掘还没有实现。相反，每个人随机选择固定数量的图像为每批。与其他两种损失相比，这种信息较少的采样策略可能会造成磁体损失

During all runs the triplet loss has been monitored as an additional information source on training behavior. Figure 4b plots the triplet loss as a function of training iterations. Note that the triplet loss has not been used as a training objective in runs softmax (cosine) and magnet. Nevertheless, both minimize the triplet loss indirectly. In particular the softmax classifier is quite efficient at minimizing the triplet loss. During iterations 20,000 to 40,000 the triplet loss drops even slightly faster when optimization is carried out with the softmax classifier rather than optimizing the triplet loss directly. Therefore, the cosine softmax classifier effectively enforces a similarity metric onto the representation space.

在所有的运行过程中，三联体损耗都被监测作为训练行为的额外信息源。图4b描绘了三元组损失作为训练迭代的函数。请注意，在softmax (cos)和magnet测试中，三片损耗并没有被用作训练目标。然而，两者都间接地减少了三联体的损失。特别是softmax分类器在最小化三重态损失方面非常有效。在20000到40000次迭代中，使用softmax分类器进行优化比直接优化三重态损失下降得更快。因此，cossoftmax分类器有效地在表示空间上强制一个相似性度量。

Figure 4: Plot (a) shows the rank 1 matching accuracy on the validation set as a function of training iterations. Plot (b) shows how the triplet loss evolves on the training set. Note that the triplet loss is only used as training objective for the triplet network. For the other two methods the loss is only monitored to obtain insight into the training behavior. 图4：图（a）显示了验证集上的等级1匹配精度与训练迭代的关系。图（b）显示了三联体损失在训练集上的演变情况。请注意，三联体损失只被用作三联体网络的训练目标。对于其他两种方法，损失的监测只是为了获得对训练行为的深入了解。

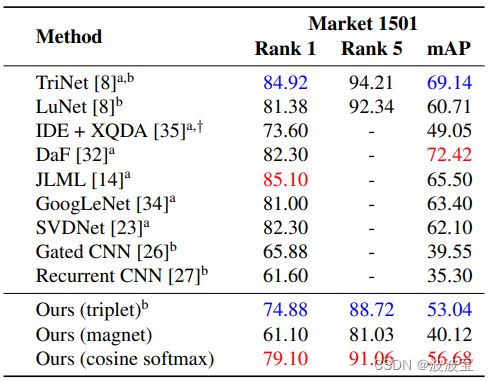
Re-Identification Performance All three networks have been evaluated on the provided test splits of the Market 1501 and MARS datasets. Table 2 and 3 summarize the results and provide a comparison against the state of the art. The training behavior and rank 1 matching rates that have been observed on the validation set manifest in the final performance on the provided test splits. Of our own networks, on both datasets the cosine softmax network achieves the best results, followed by the siamese network. The gain in mAP due to the softmax loss is 3.64 on the Market 1501 dataset and 2.58 on the MARS dataset. This is a relative gain of 6.8% and 4.7% respectively. The state of the art contains several alternative siamese architectures that have been trained with a contrastive or triplet loss, marked by b in Table 2 and 3. The performance of these networks is not always directly comparable, because the models have varying capacity. However, the LuNet of Hermans et al. [8] is a residual network with roughly double the capacity of the proposed architecture. The reported numbers have been generated with test-time data augmentation that accounts for approximately 3 mAP points according to the corresponding authors. Thus, the proposed network comes in close range at much lower capacity. Further, the method of [35] refers to a CaffeNet that has been trained with the conventional softmax classifier and the metric subspace has been obtained in a separate post processing step. The results suggest that the proposed joint classification and metric learning framework not only enforces a metric onto the representation space, but also that encoding the metric directly into the classifier works better than treating it in a subsequent post processing step.

所有三个网络都已在Market 1501和MARS数据集的测试片段上进行了评估。表2和表3总结了结果，并提供了与最新技术的比较。在提供的测试分割上的最终性能中，在验证集清单上观察到的训练行为和秩1匹配率。在我们自己的网络中，在两个数据集上，cos softmax网络的效果最好，其次是暹罗网络。由于softmax损失，mAP的收益在Market 1501数据集上为3.64，在MARS数据集上为2.58。相对涨幅分别为6.8%和4.7%。目前的技术水平包括几种可供选择的连体结构，它们都经过了对比或三重损失的训练，表2和表3中的b标记了它们。这些网络的性能并不总是可以直接比较的，因为模型的容量是不同的。然而，Hermans等人[8]的LuNet是一个剩余网络，其容量大约是所提议的体系结构的两倍。报告的数字是通过测试时间数据扩展生成的，根据相应作者的说法，这些数据大约占了3个mAP点。因此，拟议的网络以低得多的容量进入近距离。[35]方法指的是用传统的softmax分类器训练过的CaffeNet，并且在单独的后处理步骤中得到了度量子空间。结果表明，提出的联合分类和度量学习框架不仅在表示空间上强制一个度量，而且将度量直接编码到分类器中比在后续处理步骤中处理它效果更好

Table 2: Performance comparison on Market 1501 [36]. †: Numbers taken from [8]. Methods below the line show our network architecture trained with different losses. a : Pretrained on ImageNet. b: Siamese network. 表2：Market 1501的性能比较[36]。†: 数字取自[8]。线条下面的方法显示了我们用不同损失训练的网络结构。 a : 在ImageNet上预训练。b : 连体网络。

The best performing method on Market 1501 has a 15.84 points higher mAP score than the cosine softmax network. On MARS, the best performing method achieves a 10.82 higher mAP. This is a large-margin improvement over the proposed network, which shows that considerate improvement is possible by application of larger capacity architectures with additional pre-training. Note that, for example, the TriNet [8] is a ResNet-50 [6] with 25.74 million parameters that has been pre-trained on ImageNet [11]. With roughly a tenth of the parameters, our network has much lower capacity. The best performing network that has been trained from scratch, i.e., without pre-training on ImageNet, is the LuNet of Hermans et al. [8]. With approximately 5 million parameters the network is still roughly double the size, but the final model performance in terms of mAP is only 4.03 and 3.6 points higher (including test-time augmentation). Therefore, the proposed architecture provides a good trade off between computational efficiency and reidentification performance.

在Market 1501上表现最好的方法比cossoftmax网络的mAP得分高15.84分。在MARS上，表现最好的方法实现了10.82更高的mAP。这是对拟议网络的大幅改进，这表明，通过应用更大容量的体系结构和额外的预培训，可以实现考虑周到的改进。注意，例如，TriNet[8]是一个ResNet-50[6]，具有2574万个参数，这些参数已经在ImageNet[11]上进行了预训练。只有大约十分之一的参数，我们的网络容量要低得多。从零开始训练，即没有在ImageNet上进行预先训练的，性能最好的网络是Hermans等人的LuNet[8]。在大约500万个参数的情况下，网络的规模仍然是之前的两倍左右，但最终的模型性能在mAP方面只提高了4.03分和3.6分(包括测试时间的增加)。因此，提出的体系结构提供了计算效率和再识别性能之间的良好权衡

Table 2: Performance comparison on Market 1501 [36]. †: Numbers taken from [8]. Methods below the line show our network architecture trained with different losses. a : Pretrained on ImageNet. b: Siamese network. 表2：Market 1501的性能比较[36]。†: 数字取自[8]。线条下面的方法显示了我们用不同损失训练的网络结构。 a : 在ImageNet上预训练。b : 连体网络。

Learned Embedding Figure 1 and 5 show a series of exemplary queries computed from the Market 1501 test gallery. The queries shown in Figure 1 represent a selection of many identities that the network successfully identifies by nearest neighbor search. In many cases, the feature representation is robust to varying poses as well as changing background and image quality. Figure 5 shows some challenging queries and interesting failure cases. For example, in the second row the network seems to focus on the bright handbag in a low-resolution capture of a woman. The top five results returned by the network contain four women with colorful clothing. In the third row the network fails to correctly identify the gender of the queried identity. In the last example, the network successfully re-identifies a person that is first sitting on a scooter and later walks (rank 4 and 5), but also returns a wrong identity with similarly striped sweater (rank 3). A visualization of the learned embedding on the MARS test split is shown in Figure 6.

图1和图5显示了从Market 1501测试库计算出的一系列示例性查询。图1所示的查询表示网络通过最近邻居搜索成功识别的许多身份的选择。在许多情况下，特征表示对不同姿态以及背景和图像质量的变化具有鲁棒性。图5显示了一些具有挑战性的查询和有趣的失败案例。例如，在第二排，网络似乎集中在明亮的手提包在一个低分辨率捕获的女人。该网站返回的前五名搜索结果中，有四名身穿彩色服装的女性。第三行，网络无法正确识别所查询身份的性别。在最后一个例子,网络成功之后一个人坐在摩托车,后来走(等级4和5),但也返回一个错误的身份与类似的条纹毛衣(等级3)。学会了嵌入在MARS 的可视化测试分割如图6所示。

6. Conclusion

We have presented a re-parametrization of the conventional softmax classifier that enforces a cosine similarity on the representation space when trained to identify the individuals in the training set. Due to this property, the classifier can be stripped of the network after training and queries for unseen identities can be performed using nearest-neighbor search. Thus, the presented approach offers a simple, easily applicable alternative for metric learning that does not require sophisticated sampling strategies. In our experiments, training in this regime provided a modest gain in test performance. While the method itself is general, our evaluation was limited to a very specific application using a single light-weight CNN architecture. In future work, the approach should be further validated on more datasets and application domains. Such an evaluation should also include larger capacity architectures and pre-training on ImageNet.

我们提出了传统softmax分类器的一个重新参数化，该分类器在训练识别训练集中的个体时，强制表示空间上的余弦相似度。由于这个属性，分类器可以在训练后从网络中剥离，并且可以使用最近邻居搜索执行对不可见身份的查询。因此，本文提出的方法为度量学习提供了一个简单、容易适用的替代方法，不需要复杂的抽样策略。在我们的实验中，这种模式下的训练在测试表现上提供了适度的提高。虽然该方法本身是通用的，但我们的评估仅限于使用单一轻量级CNN架构的非常具体的应用。在未来的工作中，该方法应该在更多的数据集和应用领域进行进一步的验证。这种评估还应该包括更大容量的架构和ImageNet的预培训。

Figure 5: Failure cases on example queries generated from Market 1501 [36] test gallery. For each query image the five most similar and dissimilar images are shown. 图5：Market 1501[36]的测试图库中产生的失败案例。对于每张查询图片，都有五张显示了最相似和最不相似的图像。

Figure 6: Excerpt of the learned embedding on the MARS test split generated with t-SNE [25]. 图6：在MARS上学习嵌入的摘录用t-SNE[25]生成的测试分割图。

References

[1] E. Ahmed, M. Jones, and T. K. Marks. An improved deep learning architecture for person re-identification. In CVPR, pages 3908–3916, 2015.
[2] C. M. Bishop. Pattern Recognition and Machine Learning. Springer, New York, NY, 2006.
[3] S. Chopra, R. Hadsell, and Y. LeCun. Learning a similarity metric discriminatively, with application to face verification. In CVPR, pages 539–546, 2005.
[4] D.-A. Clevert, T. Unterthiner, and S. Hochreiter. Fast and accurate deep network learning by exponential linear units (ELUs). In ICLR, pages 1–14, 2015.
[5] J. Donahue, Y. Jia, O. Vinyals, J. Hoffman, N. Zhang, E. Tzeng, and T. Darrell. Decaf: A deep convolutional activation feature for generic visual recognition. In ICML, pages 647–655, 2014.
[6] K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning for image recognition. In CVPR, pages 770–778, 2016.
[7] K. He, X. Zhang, S. Ren, and J. Sun. Identity mappings in deep residual networks. In ECCV, pages 630–645, 2016.
[8] A. Hermans, L. Beyer, and B. Leibe. In defense of the triplet loss for person re-identification. arXiv preprint arXiv:1703.07737, 2017.
[9] D. Kingma and J. Ba. Adam: A method for stochastic optimization. In ICLR, pages 1–15, 2015.
[10] M. Koestinger, M. Hirzer, P. Wohlhart, P. M. Roth, and H. Bischof. Large scale metric learning from equivalence constraints. In CVPR, pages 2288–2295, 2012.
[11] A. Krizhevsky, I. Sutskever, and G. E. Hinton. Imagenet classification with deep convolutional neural networks. In NIPS, pages 1097–1105, 2012.
[12] D. Li, X. Chen, Z. Zhang, and K. Huang. Learning deep context-aware features over body and latent parts for person re-identification. In CVPR, pages 384–393, 2017.
[13] W. Li, R. Zhao, T. Xiao, and X. Wang. Deepreid: Deep filter pairing neural network for person re-identification. In CVPR, pages 152–159, 2014.
[14] W. Li, X. Zhu, and S. Gong. Person re-identification by deep joint learning of multi-loss classification. In IJCAI, pages 2194–2200, 2017.
[15] S. Liao, Y. Hu, X. Zhu, and S. Z. Li. Person re-identification by local maximal occurrence representation and metric learning. In CVPR, pages 2197–2206, 2015.
[16] T.-Y. Lin, M. Maire, S. Belongie, J. Hays, P. Perona, D. Ramanan, P. Dollar, and C. L. Zitnick. Microsoft COCO: Common objects in context. In ECCV, pages 740–755, 2014.
\[17] Y. Liu, J. Yan, and W. Ouyang. Quality aware network for set to set recognition. In CVPR, pages 1–10, 2017.
[18] H. Oh Song, Y. Xiang, S. Jegelka, and S. Savarese. Deep metric learning via lifted structured feature embedding. In CVPR, pages 4004–4012, 2016.
[19] O. Rippel, M. Paluri, P. Dollar, and L. Bourdev. Metric learning with adaptive density discrimination. ICLR, pages 1–15, 2016.
[20] T. Salimans and D. P. Kingma. Weight normalization: A simple reparameterization to accelerate training of deep neural networks. In NIPS, pages 901–909, 2016.
[21] F. Schroff, D. Kalenichenko, and J. Philbin. Facenet: A unified embedding for face recognition and clustering. In CVPR, pages 815–823, 2015.
[22] A. Sharif Razavian, H. Azizpour, J. Sullivan, and S. Carlsson. Cnn features off-the-shelf: an astounding baseline for recognition. In CVPR Workshops, pages 806–813, 2014.
[23] Y. Sun, L. Zheng, W. Deng, and S. Wang. Svdnet for pedestrian retrieval. In ICCV, pages 3800–3808, 2017.
[24] Y. Taigman, M. Yang, M. Ranzato, and L. Wolf. Deepface: Closing the gap to human-level performance in face verification. In CVPR, pages 1701–1708, 2014.
[25] L. Van Der Maaten. Accelerating t-sne using tree-based algorithms. JMLR, 15(1):3221–3245, 2014.
[26] R. R. Varior, M. Haloi, and G. Wang. Gated siamese convolutional neural network architecture for human reidentification. In ECCV, pages 791–808, 2016.
[27] R. R. Varior, B. Shuai, J. Lu, D. Xu, and G. Wang. A siamese long short-term memory architecture for human reidentification. In ECCV, pages 135–153, 2016.
[28] K. Q. Weinberger and L. K. Saul. Distance metric learning for large margin nearest neighbor classification. JMLR, 10(Feb):207–244, 2009.
[29] Y. Wen, K. Zhang, Z. Li, and Y. Qiao. A discriminative feature learning approach for deep face recognition. In ECC, pages 499–515, 2016.
[30] N. Wojke, A. Bewley, and D. Paulus. Simple online and realtime tracking with a deep association metric. In ICIP, pages 3645–3649, 2017.
[31] T. Xiao, H. Li, W. Ouyang, and X. Wang. Learning deep feature representations with domain guided dropout for pperson re-identification. In CVPR, pages 1249–1258, 2016.
[32] R. Yu, Z. Zhou, S. Bai, and X. Bai. Divide and fuse: A re-ranking approach for person re-identification. In BMVC, pages 1–13, 2017.
[33] S. Zagoruyko and N. Komodakis. Wide residual networks. In BMVC, pages 1–12, 2016.
[34] L. Zhao, X. Li, J. Wang, and Y. Zhuang. Deeply-learned part-aligned representations for person re-identification. In ICCV, pages 3219–3228, 2017.
[35] L. Zheng, Z. Bie, Y. Sun, J. Wang, C. Su, S. Wang, and Q. Tian. MARS: A video benchmark for large-scale person re-identification. In ECCV, pages 868–884, 2016.
[36] L. Zheng, L. Shen, L. Tian, S. Wang, J. Wang, and Q. Tian. Scalable person re-identification: A benchmark. In ICCV, pages 1116–1124, 2015.
[37] L. Zheng, H. Zhang, S. Sun, M. Chandraker, and Q. Tian. Person re-identification in the wild. In CVPR, 2017.
[38] Z. Zhou, Y. Huang, W. Wang, L. Wang, and T. Tan. See the forest for the trees: Joint spatial and temporal recurrent neural networks for video-based person re-identification. In CVPR, pages 4747–4756, 2017.