2021SC@SDUSC软件工程应用与实践08----GNN基础及代码实现
2021SC@SDUSC
一,背景
CNN是提取图片特征的成熟方法,基于CNN的变式也很多,通过随机卷积核的卷积操作,提取出某种特征,在通过反向传播优化卷积核,就可以提取出高精度的特征,因为其简洁与优秀,在很多领域都有用到。但现实中的大多数数据都是通过图的形式存储的,区别于图片的规则矩阵,图的形式是非格式化的,因此,类比于CNN,也需要一种基于图的卷积操作,来提取图类型数据的特征,这就是GNN。
二,参考资料
以下资料很好的囊括了从GNN基础知识到代码实现,以及原码分析等诸多方面,推荐参考
一文读懂图卷积GCN - 知乎
图神经网络库PyTorch geometric(PYG)零基础上手教程 - 知乎
torch_geometric.data — pytorch_geometric 2.0.2 documentation
从代码的角度深入浅出图神经网络(GNN)第一期_哔哩哔哩_bilibili
零基础多图详解图神经网络(GNN/GCN)【论文精读】_哔哩哔哩_bilibili
三,原理讲解
1,GNN类型
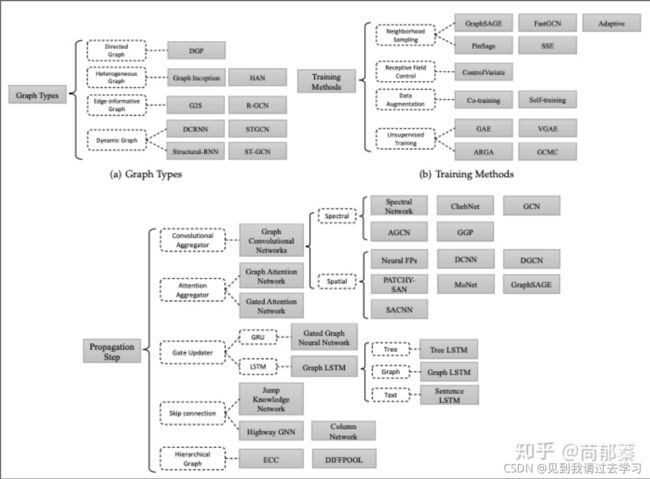
与CNN类似,GNN也有一种基础的模型,根据图的类型,训练方式,传播的方式可以分为以上的许多类型。以上的所有模型都可以统称为GNN,接下来主要讲下GNN的基础模型。
2,关于GNN
①什么可以表示成图?
1,图片表示成图
可以将图中每一个像素表示成一个点,像素和相邻像素连一条边
2,文本句子表示成图
可以把每一个词表示成一个点,文本顺序表示成边
3,分子图表示成图
4,甚至以图中人物为点,人之间的关系为边
。。。。
总之就是多种多样,同一事物,都可能表示成不同的图
②图的定义
③GNN的工作
就像前文所提到的那样,GNN主要是提取图的特征的,大体可以分为
1)提取图顶点的特征
2)提取边的特征
3)提取代表整个图的整体特征
3,GNN原理
①思路
对于图中顶点的特征,我们很容易想到邻居节点对他的影响,以及边对他的影响,GNN,就可以通过当前节点特征加上各个邻居特征,作为一层训练后的新特征,邻居也会找邻居的邻居,依次类推,最终理论上,一个点能整合所有点的特征。我们的GNN大致就是按这个思路搭建的。
②图相关矩阵定义
③图卷积的通式
针对第三种形式的归一化,目的是为了防止某个点的度太大从而增大了它的影响力,我们目前仅需要它关联其他点来更新自己特征而已。
四,代码分析
1,环境配置
我们主要通过pytorch_geometirc框架来搭建GNN,因此需要配置的库也比较少。
①pytorch
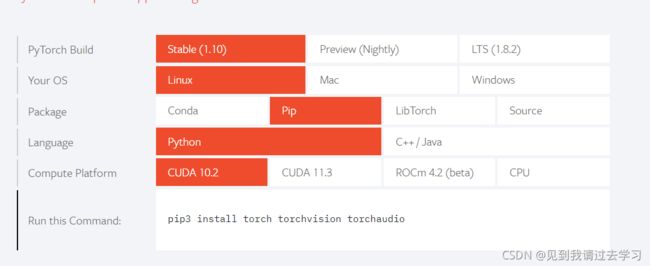
直接到官网:PyTorch 在中间部分,选用自己适配的选项,就可以安装
②pytorch_geometric
也直接到官网:Installation — pytorch_geometric 2.0.2 documentation 选择自己适配的选项,注意这里的Pytorch是1.10版本及以上
二,编码
接下来将从一个简单的GNN来讲解
需要torch中的一些函数来实现dropout,relu等等
引入GCNConv作为卷积层
我们写的GNN需要继承于torch.nn.module
import torch
import torch.nn.functional as F
from torch_geometric.nn import GCNConv这里使用torch_geometric自带的一个数据集
#数据集加载
from torch_geometric.datasets import Planetoid
dataset = Planetoid(root='/tmp/Cora', name='Cora')
print(len(dataset))这里定义了两个卷积层,conv1和conv2,从conv1中出来的数据会送到conv2中。
这里的dropout方法是为了防止过拟合,它的作用是,有一定概率(我们定),让当前这个神经元在这次循环时不工作。
relu就是激活函数了,便于求梯度
#网络定义
class Net(torch.nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = GCNConv(dataset.num_node_features, 16) # num_node_features表示一个节点几个特征
self.conv2 = GCNConv(16, dataset.num_classes)# num_classes指数据库有几个类
def forward(self, data):
x, edge_index = data.x, data.edge_index
x = self.conv1(x, edge_index)
x = F.relu(x)
x = F.dropout(x, training=self.training) # 归一化注意系数的丢失概率
x = self.conv2(x, edge_index)
return F.log_softmax(x, dim=1)
这里是选择用CPU还是GPU来计算
# 选定GPU还是CPU
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
model = Net().to(device)
data = dataset[0].to(device)这里还有些疑惑,似乎给定了两种梯度下降的方式?
# 组装好模型 这里既有学习率也有权重衰减值?
optimizer = torch.optim.Adam(model.parameters(), lr=0.01, weight_decay=5e-4)训练模型,200轮,optimizer.zero_grad()确定梯度下降来反向传播,并制定nll_loss损失函数。
#网络训练
model.train()
for epoch in range(200):
optimizer.zero_grad() # 表明是梯度下降法?
out = model(data)
loss = F.nll_loss(out[data.train_mask], data.y[data.train_mask])
loss.backward()
optimizer.step()因为该数据集仅有一个图(但有3000多个节点,是一个很复杂的图),我们这里用符合预测的节点的特征/所有节点数来算一个预测准确率。
#测试
model.eval()
_, pred = model(data).max(dim=1)
correct = float(pred[data.test_mask].eq(data.y[data.test_mask]).sum().item())
acc = correct / data.test_mask.sum().item()
print('Accuracy: {:.4f}'.format(acc))最终的测试结果也有82%的准确度
四,总结
以上便是本次报告的全部内容,如有问题,欢迎在评论区指出。