AI 数学基础知识-方向导数与梯度、范数矩阵、SVD分解、PCA、凸函数
原课程链接
自己的课程笔记,方便自己查漏补缺。想补充数学预备知识的友友,建议去看原视频。
相比于考研数学,这里更注重理解,而不是强调计算能力。
数分
方向导数和梯度
之后学梯度下降算法需要,考研时没学留下的坑,赶紧补




下面又通过一个案例计算说明:梯度方向的方向导数=梯度的模

线性代数
a = np.array([[1, 2, 3], [4, 5, 6]])
b = np.array([[1, 2, 1], [2, 2, 1]])
#点对点相乘
np.multiply(a, b)
#数学定义上的矩阵相乘
c = a.dot(b)
数学计算上,一个二维数组和一个一维数组是无法相加的。因为它们的位置无法一一对应。但是 NumPy 为我们提供了一种可以实现大小不同的数组相加的机制叫做广播机制。计算时,计算机自动使用广播机制。
#4维的单位矩阵
np.identity(4)
a = np.array([[1, 2], [3, 4]])
np.linalg.inv(a) #矩阵的逆
print(a.T) #矩阵的转置
print("a的行列式为", np.linalg.det(a)) #行列式,行列式为0,则为不可逆矩阵
print("按列向量计算 a 的范数", np.linalg.norm(a, axis=0)) # 按列向量计算范数
print("按行向量计算 a 的范数", np.linalg.norm(a, axis=1)) # 按列向量计算范数
print("计算矩阵 a 的范数", np.linalg.norm(a)) # 按列向量计算范数
print("Tr(a):", np.trace(a)) #矩阵的迹即为矩阵的对角元素(即对角线上的所有元素)之和,记作 ()
范数
用到范数来衡量向量的大小。范数的形式有很多种,而机器学习中经常使用的是 L2 范数,又称做欧几里得范数。该范数的计算公式如下: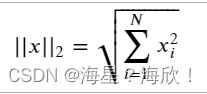
L2 范数其实就是绝对值的平方和再开方。L2 范数除来被应用于传统机器学习中,如岭回归、贝叶斯推断等,还被广泛应用于深度学习中。如利用 L2 范数进行的正则化,可以很好的缓解神经网络权重的衰减,提高模型的泛化能力。
# 函数传入的是对角线上的值
x = np.diag((1, 2, 3, 4))
# 随机初始化 25 个数,然后将这一组数转换为 5*5 的矩阵
x = np.random.randn(25).reshape(5, 5)
x
cov_up = np.triu(x) #利用 triu()函数取出矩阵 x 的上三角矩阵
cov_up
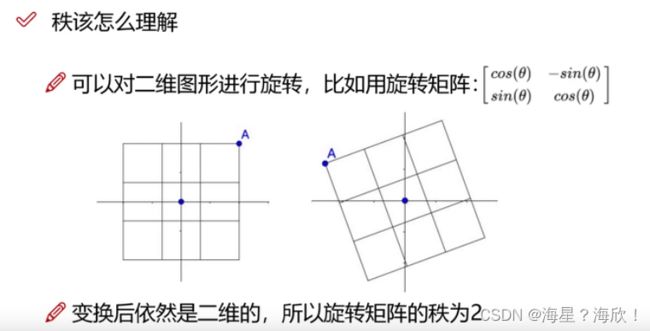
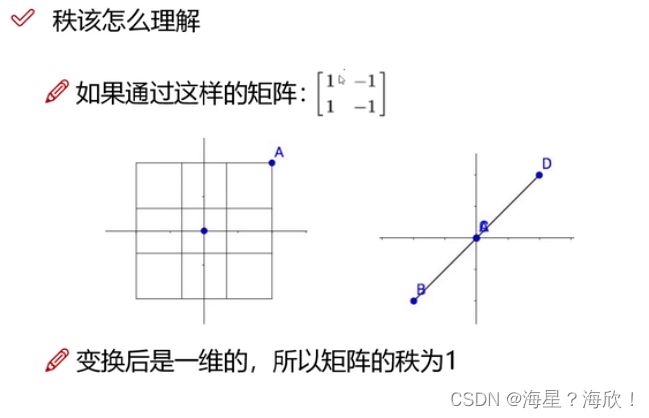
矩阵的秩理解

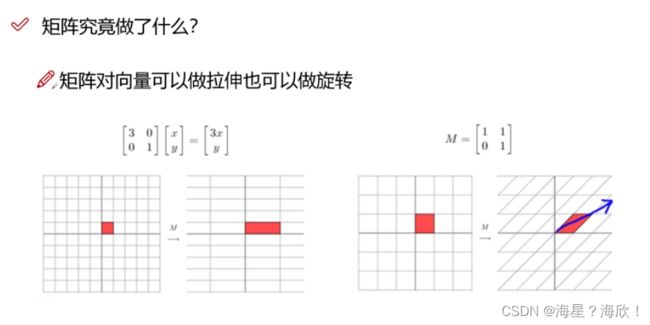
特征值与特征向量
理解:拳击中,击打方向是特征向量,击打的力是特征值。特征值越大说明该特征向量更重要。特征值大的是主要信息。—降维会用到

矩阵乘以向量,指对该向量做旋转和拉伸
而特征向量指和矩阵相乘后,向量只发生伸缩而无旋转,伸缩值即特征值
使用 vals,vecs = np.linalg.eig(x) 函数来完成特征分解
a = np.array([[1, 2, 3], [5, 8, 7], [1, 1, 1]])
e_vals, e_vecs = np.linalg.eig(a)
print("特征值为:", e_vals)
print("特征向量为:\n", e_vecs)
特征分解其实就是将原矩阵中的向量方向和距离进行了分离。我么可以得到每个特征向量上的特征值,进而比较每组向量(特征向量+特征值)对原矩阵内容的贡献程度。
每个特征值占总特征值的百分比进而估算每个特征向量对原矩阵的贡献程度(这里的特征值都需要先进行绝对值,再求和。因为这里的正负号,表示的只是方向而已)
pro = abs(e_vals)/np.sum(abs(e_vals))
pro
我们就可以把那些对原矩阵内容贡献程度较小的 特征值+特征向量 给删除掉,达到降维的目的。即在保存原数据大部分内容的情况下,缩小数据量,减少数据特征的过程
SVD分解
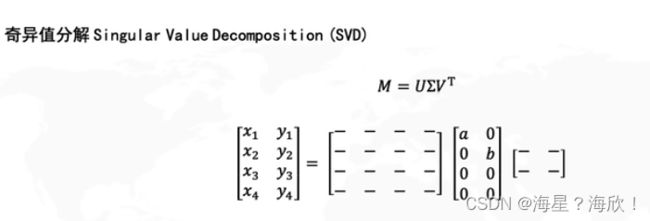
其中 中间的矩阵为对角矩阵,而它对角线上的元素就被称之为奇异值。矩阵 的列向量被称之为「左奇异向量」,矩阵 的列向量被称之为「右奇异向量」。当我们需要对矩阵的行数进行压缩时,我们使用到的组合就是:左奇异向量 + 奇异值。当我们是对矩阵的列数进行压缩降维时,我们使用到的就是:右奇异向量 + 奇异值。
使用 np.linalg.svd(a) 函数 对矩阵 进行奇异值分解,得到三个返回值:矩阵 M 的左奇异向量 、对角矩阵 的对角线上的值、矩阵 的右奇异向量 的转置
a = np.array([[1, 2, 3, 4], [5, 8, 6, 7], [1, 1, 1, 2]])
u, s, vh = np.linalg.svd(a) # vh 表示 v 的转置
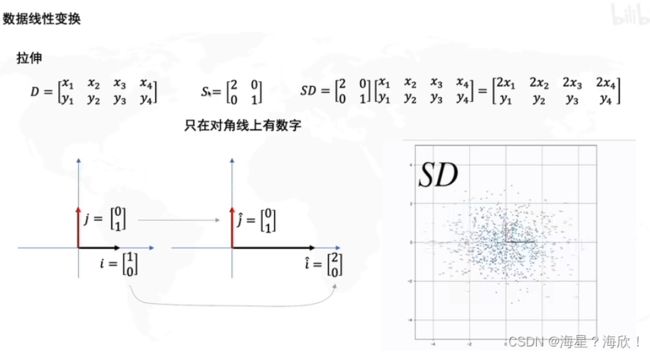
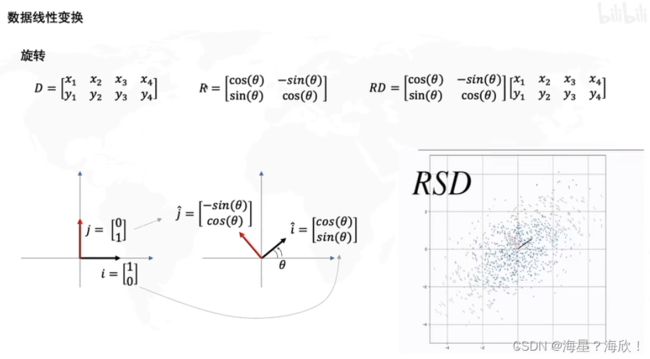
逆时针旋转角度seita
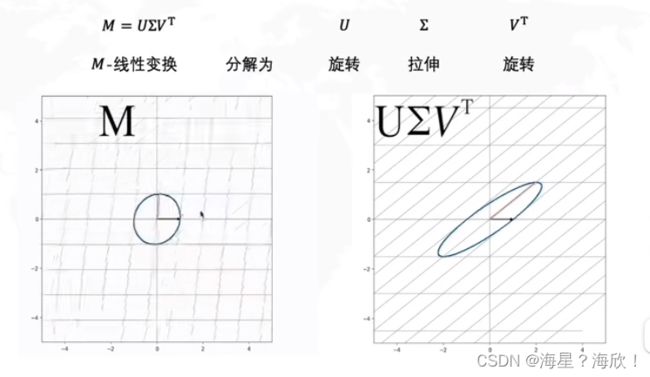
即SVD分解将原本旋转拉伸一步到位的矩阵M,分解成旋转-拉伸-旋转 。
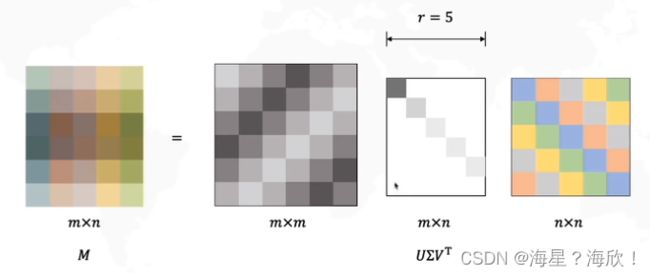
r原本为m,但也可以去掉不重要的奇异值,达到压缩的目的。即r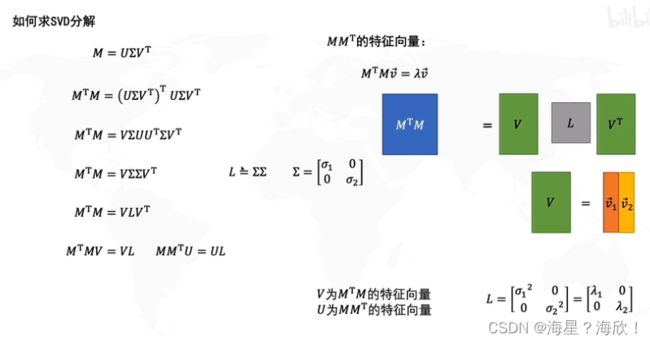
求解U、V、y以及奇异值的方法
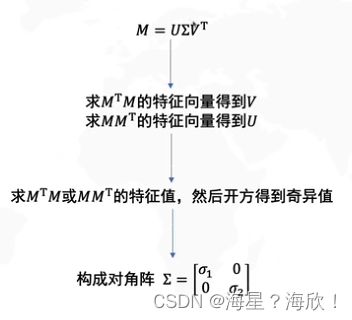
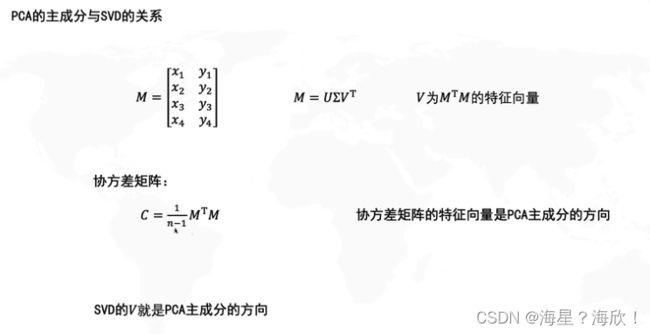
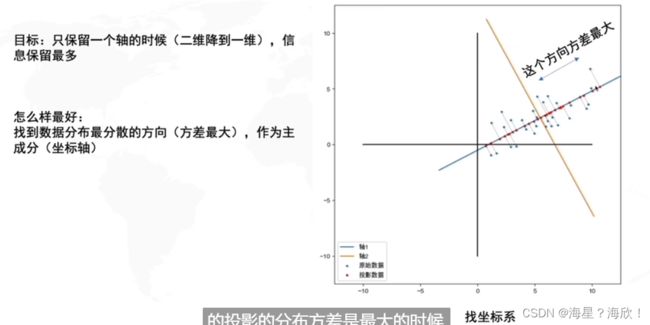
主成分分析PCA
是一种数据降维的算法
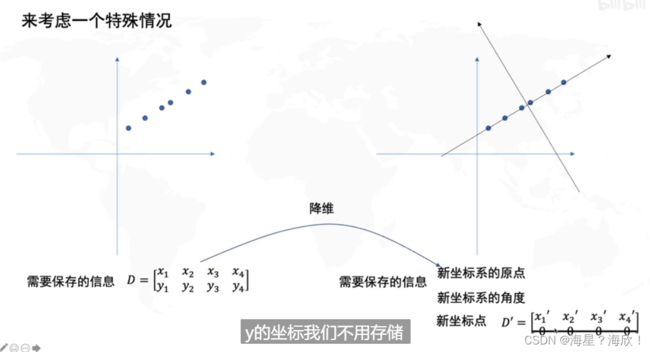
方差最大,也就是投影到这一个轴后,也能很好的区分不同的点数据
概率论
最优化问题
基本概念
最优化问题统一表示为最优化问题
约束有等式约束,不等式约束
驻点:
- 一元找最小值:求导等于0的点
- 多元找最小值:梯度等于0的点
但实际操作中不一定好求
采用迭代法:先近似求解,再不断迭代直到某点的梯度趋于0
数值优化方法
1,梯度下降法
2,牛顿法
3,坐标下降法
优化算法面临的问题:
1.局部极值问题
2.鞍点问题
凸优化问题
定义:满足变量可行域是个凸集,且目标函数是个凸函数
凸集
凸集定义:若随意取两点在集合内,则两点连线上的所有点都在集合内.
数学表达式:若x,y属于集合C,则 Qx+(1-Q)y 也属于C,其中
等式约束都是凸集
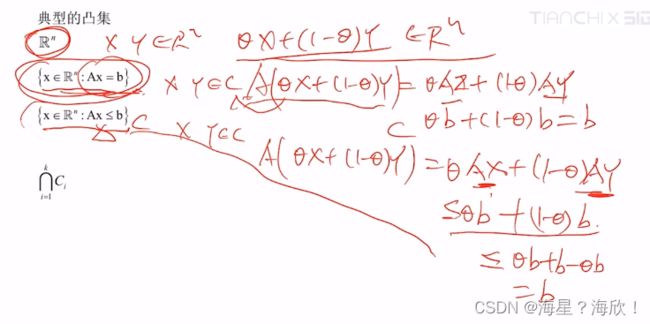
若c1,c2…ck是凸集,则他们的交集也是凸集
凸函数

对于凸优化问题,所有局部最优解一定是全局最优解
用反证法证明
拉格朗日对偶
KKT条件