机器学习中的数学知识1——导数、向量、偏导与梯度
数学是机器学习的基础,各种算法需要大量使用微积分,线性代数,概率论,最优化方法等数学知识,特别是最优化理论,可以说机器学习中的大多数算法研究到最后都是一个数学优化问题。接下来将一一介绍机器学习中的数学知识。
1.导数
导数定义为函数的自变量变化值趋向于0时,函数的变化量与自变量的变化量的比值的极限,即

如果该极限存在,则称函数在该点可导。导数的几何意义就是函数在某一点处的切线的斜率。
以下列出了各种基本函数和运算的求导公式(这些都是高中的知识点)。
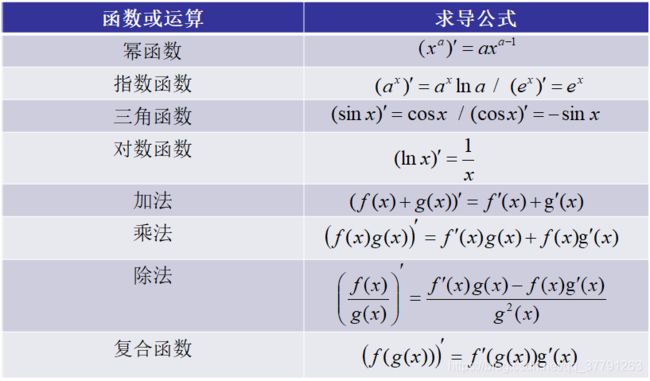
复合函数的求导公式可以推广到多层复合函数和多元复合函数,而在机器学习的最优化理论中用到最多的也是复合函数的求导。下面用一个例子来说明一下复合导数的计算方法,对于函数 f ( x ) = l n ( 1 + x 2 + e 2 x ) f(x)=ln(1+x^2+e^2x) f(x)=ln(1+x2+e2x)的导数为
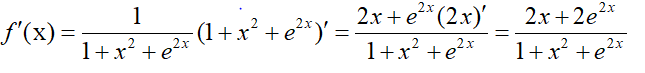
导数和函数的单调性密切相关,导数大于0时,函数单调递增,导数小于0时,函数单调递减。在极值点处导数必定为0。导数等于0的点成为函数的驻点,为函数值求解极值提供依据。
拓展
如果可以对导数继续求导,可以到高阶导数。二阶导数记为 f ′ ′ ( x ) f''(x) f′′(x),高阶导数记为 f ( n ) f^{(n)} f(n) ( x ) (x) (x)。
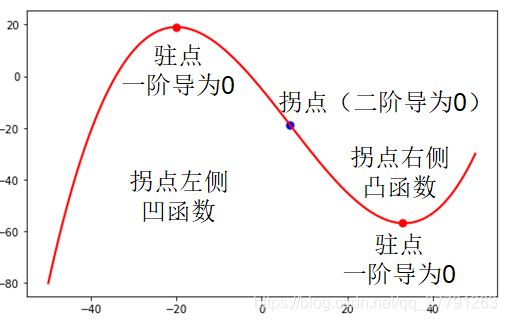
二阶导数决定了函数的凹凸性,
如果二阶导数大于0,则称函数为凸函数;
如果二阶导数小于0,则称函数为凹函数;
二阶导数等于0,并且两侧的二阶导数异号的点称为函数的拐点(改变函数凹凸性的点)。如下图所示:
根据一阶导数和二阶导数,可以得到一元函数的极值判别法:
在驻点如果二阶导数大于0,则为函数的极小值点;
如果二阶导大于0,则为函数的极大值点;
如果二阶导数等于0,情况不定。
2.向量
向量是有大小和方向的量,是由多个数构成的一维数组,每个数称为它的分量。分量的数量称为向量的维度。
n维行向量记为 x = [ x 1 , x 2 , . . . . . . , x n − 1 , x n ] ∈ R n \mathbf{x}=[x_{1},x_{2},......,x_{n-1},x_{n}]\in\mathbb{R}^n x=[x1,x2,......,xn−1,xn]∈Rn,向量的转置记为 x T x^T xT
向量的内积,定义为他们对应元素乘积的和,记作: x T y = ∑ i = 1 N x i y i \mathbf{x}^T\mathbf{y}=\sum_{i=1}^Nx_{i}y_{i} xTy=i=1∑Nxiyi
如果两个向量的内积为0,则称为它们正交。
向量的L-P范数
向量的L-P范数是一个标量,定义为
∥ x ∥ p = ( ∑ i = 1 n ∣ x i ∣ p ) 1 p \lVert x \rVert_{p}=(\sum_{i=1}^n|x_{i}|^p)^\frac{1}{p} ∥x∥p=(i=1∑n∣xi∣p)p1
其中常用的是L1和L2范数。向量L1范数为所有分量的绝对值之和,即:
∥ x ∥ 1 = ( ∑ i = 1 n ∣ x i ∣ ) \lVert x \rVert_{1}=(\sum_{i=1}^n|x_{i}|) ∥x∥1=(i=1∑n∣xi∣)
向量L2范数也称为向量的模长,即向量的长度,公式:
∥ x ∥ 2 = ( ∑ i = 1 n ∣ x i ∣ 2 ) \lVert x \rVert_{2}=(\sqrt{\sum_{i=1}^n|x_{i}|^2)} ∥x∥2=(i=1∑n∣xi∣2)
3.偏导与梯度
偏导
多元函数的偏导数是一元函数导数的推广。假设有多元函数 f ( x 1 , x 2 , . . . . . . , x n − 1 , x n ) f(x_{1},x_{2},......,x_{n-1},x_{n}) f(x1,x2,......,xn−1,xn),它们对自变量 x i x_{i} xi的偏导数定义为
∂ f ∂ x i = lim Δ x i → 0 f ( x 1 , . . . x i + Δ x i , . . . x n ) − f ( x 1 , . . . x i + , . . . x n ) Δ x i \frac{\partial f}{\partial x_{i}}=\lim_{\Delta x_{i}\to 0}\frac{f(x_{1},...x_{i}+\Delta x_{i},...x_{n})-f(x_{1},...x_{i}+,...x_{n})}{\Delta x_{i}} ∂xi∂f=Δxi→0limΔxif(x1,...xi+Δxi,...xn)−f(x1,...xi+,...xn)
具体计算时,对要求导的变量求导,把其他的变量当做常量即可,例如:
( x 2 + x y − y 2 ) x ′ = 2 x + y (x^2+xy-y^2)'_{x}=2x+y (x2+xy−y2)x′=2x+y ( x 2 + x y − y 2 ) y ′ = x − 2 y (x^2+xy-y^2)'_{y}=x-2y (x2+xy−y2)y′=x−2y
梯度
梯度是导数对多元函数的推广,他是多元函数对各个自变量的偏导数形成的向量。梯度定义为:
∇ f ( x ) = [ ∂ f ∂ x 1 , ∂ f ∂ x 2 , . . . , ∂ f ∂ x n ] T \nabla f(x)=[\frac{\partial f}{\partial x_{1}},\frac{\partial f}{\partial x_{2}},...,\frac{\partial f}{\partial x_{n}}]^T ∇f(x)=[∂x1∂f,∂x2∂f,...,∂xn∂f]T
其中 ∇ \nabla ∇表示为梯度算子它作用于一个多元函数得到一个向量。例如:
∇ ( x 2 + x y − y 2 ) = [ 2 x + y , x − 2 y ] T \nabla (x^2+xy-y^2)=[2x+y,x-2y]^T ∇(x2+xy−y2)=[2x+y,x−2y]T
梯度与函数的单调性,极值有关。可导函数在某一点处取得极值点的必要条件是梯度为0,梯度为0的点成为驻点,但是梯度为0只是函数取极值的必要条件,而不是充分条件。也就是说驻点不一定是极值点,但极值点一定是驻点。
类似的可以定义函数的高阶偏导数,这比一元函数的高阶导数复杂,因为有多个变量,以二阶导数为例:
∂ 2 f ∂ x ∂ y \frac {\partial^2 f }{\partial x \partial y} ∂x∂y∂2f
表示先对 x x x求偏导数,然后再对 y y y求偏导数。举个例子:
∂ 2 f ∂ x ∂ y ( x 2 + x y − y 2 ) = ∂ 2 f ∂ y ( 2 x + y ) = 1 \frac {\partial^2 f }{\partial x \partial y}(x^2+xy-y^2)=\frac {\partial^2 f }{ \partial y}(2x+y)=1 ∂x∂y∂2f(x2+xy−y2)=∂y∂2f(2x+y)=1
一般情况下,混合二阶偏导数与求导的次序无关,即,
∂ 2 f ∂ x ∂ y = ∂ 2 f ∂ y ∂ x \frac {\partial^2 f }{\partial x \partial y}=\frac {\partial^2 f }{\partial y \partial x} ∂x∂y∂2f=∂y∂x∂2f