MATLAB简介与矩阵定义

---

MATLAB简介

MATLAB简介

MATLAB是 matrix & laboratory 两个词的组合，意为矩阵工厂（矩阵实验室）。它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中。

MATLAB界面(以2016a为例)

实时编辑器字体的放大缩小：ctrl + 鼠标的滚轮。

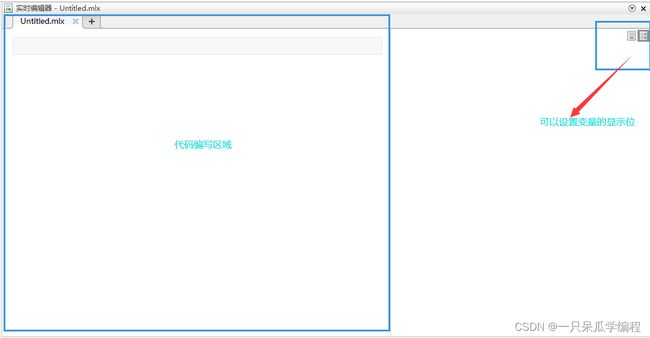
实时脚本编辑器中代码和文本切换的快捷键：alt + enter。

插入分解符，可以使代码分块运行。

注释

注释符号：%

续行符

续行符符号：...

每行结束符号

每行结束符号：;

常用函数

abs( 参数 )

求绝对值或复数的模

sqrt( 参数 )

开平方

mod( x, y )

取余
求 x 对 y 的余数

exp( 参数 )

指数函数，参数为次方

log( 参数 )

求以 e 为底的对数

log2( 参数 )

求以 2 为底的对数

log10( 参数 )

求以 10 为底的对数

三角函数

sin( x )
cos( x )
tan( x )
cot( x )
…

统计相关的函数

sum()

求和
sum( [1,2,3] )求1 2 3三数之和

mean()

求均值
mean( [1,2,3] )求1 2 3的平均值

std()

求标准差
方差：(std())^2

var()

求方差

cov()

求协方差

max()

最大值

min()

最小值

range()

极差：max() - min()

median()

中位数

mode()

众数

矩阵运算

赋值运算符

赋值运算符：=

等号运算符

等号运算符：==
返回值：相等返回 1 ，反之返回 0 。

定义空矩阵

m = []
m 是一个空矩阵。

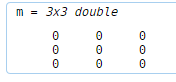
定义一个m*n的矩阵

m = [ 1 ]
m 为一个一行一列的矩阵，其中的元素为 1 。

m = [ 1 2 3 ]
m = [ 1, 2, 3 ]
m 为一个行矩阵，一行三列。
同一行的元素之间可以用逗号分割也可以使用空格进行分割。

m = [ 1; 2; 3 ]
m为一个列矩阵，三行一列。
不同行之间使用;进行分割。

m = [ 1 2 3; 4 5 6 ]
m 为一个两行三列的矩阵。

使用 冒号运算符 生成矩阵

1 : 10
生成一个一行10列的矩阵

第一个数表示矩阵开始数，第二个数表示矩阵结束的数。默认矩阵中元素的步长为1，即每个元素之间相差1，所以 1 : 10 一共生成1-10的10个数。
默认生成的矩阵为行矩阵。

1 : 0.5 : 10
生成一个1行20列的矩阵。

第一个数表示矩阵的开始，第二个数为步长，第三个数为矩阵的结束。

使用冒号运算符生成矩阵语法

m = 初始值 ：步长 ：终值
步长默认为1，所以步长为1时可以省略。

使用linspace()生成矩阵

语法：
linspace( 初始值，终值，点数 )
点数默认为100。

m = linspace(1, 10, 10)

矩阵的拼凑和变形

矩阵的拼接

m1 = [ 1 2 3 ];
m2 = [ 4 5 6 ];
m = [ m1 m2 ]
m = [ m1, m2 ]

m 为 m1 m2 进行行拼接的结果矩阵。

m1 = [ 1 2 3 ];
m2 = [ 4 5 6 ];
m = [ m1; m2 ]

m 为 m1 m2 进行列拼接的结果矩阵。

矩阵的变形

语法：
reshape( 矩阵, 要变成的形状 )

m1 = 1:10;
m2 = reshape( m1, [2, 5] )
m2 = reshape( m1, 2, 5 )

将 m1 变成 2行5列的矩阵。

特殊矩阵和随机矩阵

特殊矩阵

单位矩阵

对角线为1的方阵。
eye( n )其中为方阵的阶数。

n = 3;
m = eye( n )

全0矩阵

zeros( n )生成n阶全0的方阵。

n = 3;
m = zeros( n )

zeros( m, n )生成m*n的全0矩阵。
m为行数，n为列数。

m = 2;
n = 3;

res = zeros( m, n )
res = zeros( [m, n] )

全1矩阵

ones( n )

n = 3;

res = ones( n )

ones( m, n )

m = 2;
n = 3;

res = ones( m, n )

三维矩阵

ones( [3, 5, 2] )生成一个三维全1矩阵。
三个数分别对应 [ 行，列，页 ]。

m = ones( 3, 5, 2 )
m = ones( [3, 5, 2] )

随机数矩阵

rand()

m = 3;
n = 5;
% 生成一个n阶的方阵，其中每个元素的取值范围为0-1
rand(n)

% 生成一个m*n的矩阵，其中每个元素的取值范围为0-1
rand( m, n )
rand( [m, n] )

randi()

m = 3;
n = 5;
% 生成一个取值区间在[1,max]的整数
% randi(max)
randi(10)

% 生成一个取值区间在[1,max]的n阶方阵
% randi(max, n)
randi(10, n)

% 生成一个取值区间在[1,max]的m*n矩阵
% randi(max, m, n)
% randi(max, [m, n])
randi( 10, m, n )

randn()

randn()用法同rand()。
服从正态分布。

m = 3;
n = 5;
% 生成一个n阶的方阵
randn(n)

% 生成一个m*n的矩阵
randn( m, n )
randn( [m, n] )

在MATLAB中搜索相关函数用法