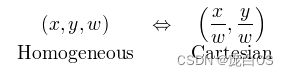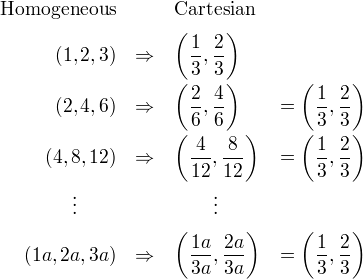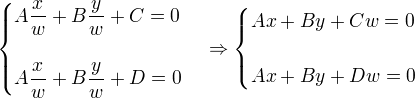openGL 3D geometry 之数学部分

以下内容是自己从各处整理出来，便于自己的理解，以便忘记后回忆恢复。

1.裁切空间

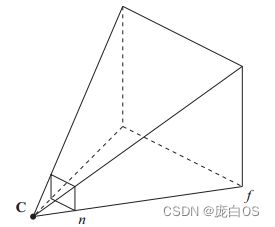
1. opengl 只会处理视椎体内的物体，f不是无穷远是因为Z深度精度问题所限，n不是o点，因为越近越大。因为视椎体的取舍，舍了完备，留下的已经足够了用了。

2.因为视椎体的原因，必然会有裁切，因此有物体就是在边界，还有一些在视椎体外。

3.理论上直接用视椎体来裁切也行，但是裁切不是那么方便，还有三角形视椎体交点插值问题。

目前用的标准方案如下：

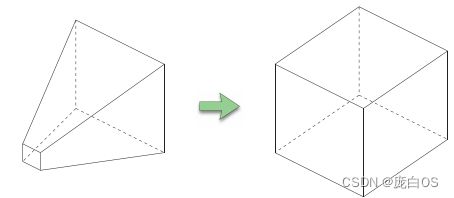
 将视椎体frustum变换为CVV（规则观察体(Canonical View Volume）。

在规则的立方体进行裁切，自然比较简单，并且这个变换就是一次matrix矩阵乘法。

之后在用逆矩阵就可以变换回来。简洁明了。

2.点，向量，齐次空间

这是重点内容，首先点和向量的问题。这其实是关键。我一开始没搞明白的根本原因就出在这里。

“齐次坐标表示是计算机图形学的重要手段之一，它既能够用来明确区分向量和点，同时也更易用于进行仿射（线性）几何变换。”—— F.S. Hill, JR。

事实上，到现在我还是有点模糊。不能想象出3D齐次空间是什么样子。

以下内容参考：

什么是齐次坐标? - 知乎

问题:两条平行线可以相交?

在欧氏空间（几何学）中，同一平面上的两条平行线不能相交，或者说不能永远相交。这是一个大家都熟悉的常识。

但是，在投影空间中就不一样了，比如，下图上的火车铁路在远离眼睛的时候会变得更窄。最后，两条平行的铁轨在地平线处相交，也就是无限远处的一点。

欧氏空间（或笛卡尔空间）能很好地描述我们的2D/3D几何，但它们不足以处理投影空间（实际上，欧氏几何是投影几何的一个子集）。一个2D点的笛卡尔坐标可以表示为（x，y）。

如果这个点远去到无穷远呢？无穷远处的点在欧氏空间中无法具体展示。在投影空间中，平行线会在无穷远处相遇，但在欧氏空间中却做不到。

那么数学家如何用数学的方法来描述这个问题呢?

解决方案: 齐次坐标

由 August Ferdinand Möbius(不错,就是那个莫比乌斯圈的那位) 提出的齐次坐标，使图形和几何学的计算在投影空间中成为可能。齐次坐标是用N+1个数来表示N维坐标的一种方式。

要制作二维齐次坐标，我们只需在现有坐标中增加一个额外的变量w。因此，笛卡尔坐标中的一点，(X，Y)在齐次坐标中就变成了(x，y，w)。而笛卡儿坐标中的X和Y在齐次坐标中的x、y和w则重新表达为

X = x/w
Y = y/w

为什么叫 “齐次”呢？

如前所述，为了将齐次坐标（x，y，w）转换为笛卡尔坐标，我们只需将x和y除以w即可。

将Homogeneous转换为Cartesian，我们可以发现一个重要的事实。让我们看看下面的例子。

如你所见 (1, 2, 3), (2, 4, 6)和(4, 8, 12)这三个点对应于同一个欧氏点(1/3, 2/3). 而任何乘以a的数（1a，2a，3a）与欧氏空间中的（1/3，2/3）是同一个点。因此，这些点是 “homogeneous/齐次 “的，因为它们在欧氏空间（或笛卡尔空间）中代表同一个点。换句话说，齐次坐标是与乘数a不相关的。

数学证明: 两条平行线可以相交

考虑以下欧氏空间的线性系统。

而我们知道，由于C≠D，所以上述方程没有解。 如果C=D，那么两条线是相同的（重叠的）。

让我们重写投影空间的方程，将x和y分别替换为x/w，y/w。

现在，我们有一个解，(x，y，0)，因为(C-D)w=0，∴w=0. 因此，两条平行线在(x，y，0)处相交.

(x,y,0)在几何上代表一条没有起点与终点, 也没有长度的射线，它只有方向。

齐次坐标的应用

齐次坐标在计算机图形学中是非常有用的基本概念，通过增加一个额外的维度W后，可以用来对几何体进行缩放,旋转,平移,透视投影的矩阵变换.

任何N维度齐次坐标，只要W不为0，都可以通过将每一个分量除以W来转换到 W=1的向量, 然后获得其N-1维的欧式空间的点值。

而当W=0时，这个坐标表示无限长的一个向量，通常表示N-1维的矢量。

齐次坐标的一个重要的优点就是能区分点和向量。简单点就是说,比如二维空间（x,y)这是个点，还是个向量？无法区分！如F.S. Hill, JR所说，在齐次坐标上就能，(x,y,1)是点，（x,y,0）是向量。

同理在3维空间，如果是点世界，那么点(x,y,z)=V+P0必然有位置信息P0。而向量(x,y,z)只是一个有大小和方向的信息，没有位置信息。也就是说，无法用(x,y,z)来同时表达3维的点与向量。如果要区分就必需要加一个维度信息。

3维世界的点集，由于参考原点的变化，构成了4维空间。就像时间流逝一样，变成4维空间。是不是很神奇？

再来展开一下点和向量：

深入探索透视投影变换_popy007的博客-CSDN博客_透视投影变换

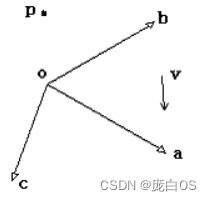
根据《向量几何在游戏编程中的使用6》中关于基的概念。对于一个向量v以及基oabc，

可以找到一组坐标(v1,v2,v3)，使得

v = v1 a + v2 b + v3 c （1）

而对于一个点p，则可以找到一组坐标（p1,p2,p3），使得

p – o = p1 a + p2 b + p3 c （2）

从上面对向量和点的表达，我们可以看出为了在坐标系中表示一个点（如p），我们把点的位置看作是对这个基的原点o所进行的一个位移，即一个向量——p – o（有的书中把这样的向量叫做位置向量——起始于坐标原点的特殊向量），我们在表达这个向量的同时用等价的方式表达出了点p:

p = o + p1 a + p2 b + p3 c (3)

(1)(3)是坐标系下表达一个向量和点的不同表达方式。这里可以看出，虽然都是用代数分量的形式表达向量和点，但表达一个点比一个向量需要额外的信息。如果我写出一个代数分量表达(1, 4, 7)，谁知道它是个向量还是个点！

我们现在把（1）（3）写成矩阵的形式：

这里(a,b,c,o)是坐标基矩阵，右边的列向量分别是向量v和点p在基下的坐标。这样，向量和点在同一个基下就有了不同的表达：3D向量的第4个代数分量是0，而3D点的第4个代数分量是1。像这种这种用4个代数分量表示3D几何概念的方式是一种齐次坐标表示。

“齐次坐标表示是计算机图形学的重要手段之一，它既能够用来明确区分向量和点，同时也更易用于进行仿射（线性）几何变换。”—— F.S. Hill, JR
————————————————
版权声明：本文为CSDN博主「popy007」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/popy007/article/details/1797121

 如上，就是一种齐次坐标表示。w=1就是我们所在的3维空间。

进一步投影空间和齐次空间是很有关系，有时候很容易模糊深度和w。没有错，它们真的有一种同构关系。(x,y,1)是一个点，那么在w=1时，就是一个点，当w->无穷大时，这个点就变成(x/无穷大，x/无穷大，1/无穷大）那么这个点就很有意思了，变成(0,0,0)，就像我们拿同样一个画，离我们越远，这个投影就越小，拿到很远时，就成了一个点。画还是那幅画，homegenuos齐次就是相同的东西生成的意思。

3 透视投影

参考自：3D游戏与计算机图形学中的数学方法

裁切非常重要，目前标准的做法是在CVV中干这事。方便算（1.容易判断是否在椎体外面，2，方便插入交点值）

推导过程：

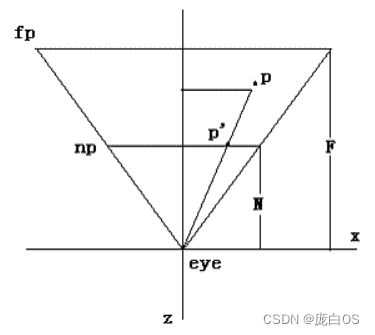
推导要领：先计算x,y的投影到CVV。然后计算Z的投影到CVV。要注意一点，这个投影必须考虑光栅化的要求，即扫描点是线性的。特别是Z值。

注意一下，这个图，说明齐次空间。 

 这两步只是简单的几何等比运算。上面是拉伸成-1,1的空间

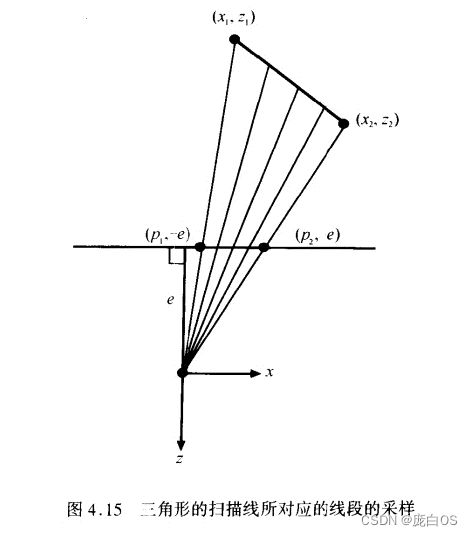
 关于Z，如果要线性插值，就必须是1/z的关系。推导如下：

 

 

 因此，此处的变换也必需是1/z关系，

 

 

 注意到一点，这个Pz就当w使用了。刚好是一致的。也就是说3维在2维屏幕上投影时，是一个齐次空间，主要是近大远小，其次有了位置信息。因为2维屏幕是容纳不了3维物体的，主个齐次空间可以理解为2D切片，将3维物体进行2D切片，并且近大远小，有一个深度信息。