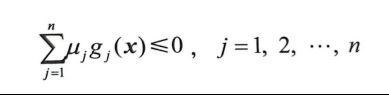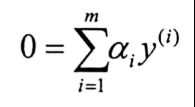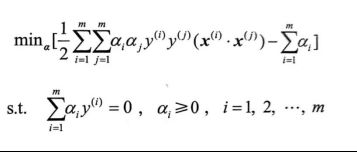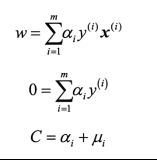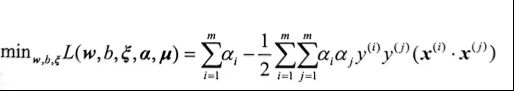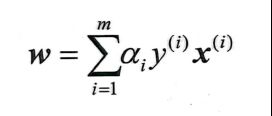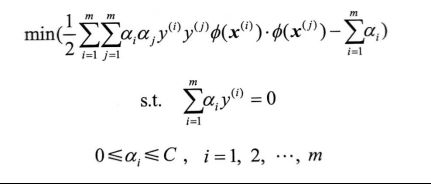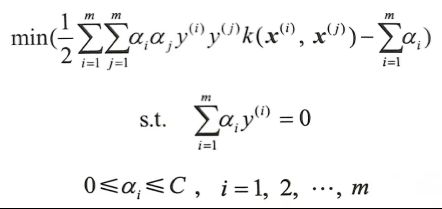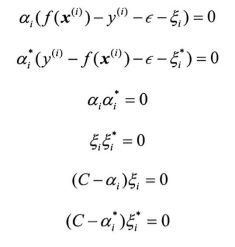机器学习极简入门笔记-3-有监督学习进阶-SVM、SVR数学原理
目录
第12章 SVM
12.1 线性可分SVM
12.2 直观理解拉格朗日乘子法和KKT条件
12.3 对偶学习算法
12.3.1 对偶问题
12.3.2 强对偶性
12.4 求解线性可分SVM的目标函数
12.4.1 线性可分SVM的主问题
12.4.2 使用对偶算法求解线性可分SVM的步骤
12.5 线性SVM,间隔由硬到软
12.5.1 线性SVM的主问题
12.6.3 线性SVM的支持向量
12.6 非线性SVM和核函数
12.6.1 非线性SVM
12.6.2 核函数
12.6.3 数据归一化
第13章 SVR
13.1 宽容的SVR
13.1.1 模型函数
13.1.2 原理
13.1.3 两个松弛变量
13.2 SVR的主问题和对偶问题
13.3 支持向量与求解线性模型参数
-
第12章 SVM
12.1 线性可分SVM
怎么找到最大间隔超平面呢?
我们可以先找到两个平行的、能够分离正负例1的辅助超平面,然后将它们分别推向正负例两侧,让它们之间的距离尽可能大,直到有至1少一个正样本或者负样本通过对应的辅助超平面,即“推到无法再推”,再推就“过界”。
这两个辅助超平面互相平行,它们中间没有样本的区域称为“间隔”,最大间隔超平面位于这两个辅助超平面的正中间并与它们平行。
以二维情况为例
目标函数
本书中未对目标函数进行明确推导,为了降低阅读门槛,只推导了二维空间的情形
而且没有使用点到面距离公式,也未明确说明距离表达式中对分子进行放缩的过程
故略去相关内容。
详细解释请移步【浙江大学机器学习胡浩基】02 支持向量机_南鸢北折的博客-CSDN博客
12.2 直观理解拉格朗日乘子法和KKT条件
推荐看看马同学的相关文章
如何理解拉格朗日乘子法?_马同学图解数学的博客-CSDN博客_拉格朗日乘子法原理
为什么相切?反过来想,如果它们不相切的会怎样?要么不相交,这样的话 g(x,y)=0就没法约束f(x,y)了。要么有两个交点,如果这样,我们可以再作 f(x,y)的另一条等高线,让新等高线和g(x,y)=0相切,取切点为(x*,y*)。如此一来,它们仍在(x*,y*)处相切。
那么,带有不等式约束的优化问题如何解决?
推荐看看文章
【数学】拉格朗日对偶,从0到完全理解_frostime的博客-CSDN博客_拉格朗日对偶
在这篇文章中,对于为何限制λ≥0,在3.5节中做出了解释
但没有给出直观解释。这里刚好依据本书中的思路解释一下
当条件是g(x,y)≤0时,我们可以把它拆分成g(x,y)=0和g(x,y)<0 两种情况来看。
先各取一个极小值,再比较哪个更小,使用最小的那个
对于g(x, y)<0
“<0”是一个区间,对应到三维坐标中不再是某个固定的曲面。在这种情况下,如果 f(x,y)的极小值就在这个区间里,那么直接对f(x,y)求无约束的极小值就好了。
对应到拉格朗日函数就是:令λ=0,直接通过令f(x,y)的梯度为0求f(x,y)的极小值。求出极小值f(x,y)之后,再判断(x,y)是否符合约束条件。
对于g(x,y)=0
可以参考等式约束条件的做法。
有一点要注意,在仅有等式约束条件时,我们设f’(x,y)+λg’(x,y)=0,只要常数λ≠0即可
但是在以从g(x,y)≤0中拆分出来的等式为约束条件时,我们要求:存在常数λ>0
这是为什么呢?我们来可视化地看一下不等式约束的两种情况
(黑点表示最终满足约束条件的函数极小值)
若是左侧的情况,即g(x,y)<0的区域包含了f(x,y)的极小值点,此时可以直接求f(x,y)的极小值
若是右侧情况,即g(x,y)<0的区域不包含了f(x,y)的极小值点,此时整体的极小值点在g(x,y)=0的某处取到
下面用数学方式来描述
回想一下函数梯度的物理意义:实际上,一个函数在某一点的梯度方向(向量方向)指明了该函数的函数值沿着自变量增长的方向变化的趋势。
现在已知(x*,y*)为最小值点,那么我们在g(x,y)的梯度方向上前进一个微小的长度,到达点(x**,y**),则g(x**,y**)>g(x*,y*)。
而g(x*,y*)=0,根据梯度的物理意义,则(x*,y*)点处g(·)函数的梯度方向指向的是g(x,y)>0的区域。
而约束条件却是g(x,y)<0,那说明不等式约束条件所对应的区域与(x*,y*)点处g(·)函数的梯度方向是相反的。
现在考虑图右侧的情况,此时f(·)函数带约束条件的极小值点(x*,y*)就位于g(x,y)=0对应的曲线上。而(x,y)点处f(·)函数的梯度方向正是f(·)函数本身的增量方向,因此在g(x,y)<0所在的区域对应的应该是f(x,y)的递增方向,如若不然,就应该是图左侧的情况了。
因此,只有当f(x,y)梯度方向和g(x,y)<0区域所在方向相同,也就是和(x*,y*)点处 g(·)函数梯度方向相反,f(x,y)的约束条件极小值才会出现在g(x,y)=0的曲线上。
所以,在这种情况下,存在常数λ>0,使得f’(x*,y*)=-λg’(x*,y*),进一步可以导出:
f'(x*,y*)+λg’(x*,y*)=0,λ>0
下面将之前拆开的两种情况合起来
- 如果严格不等式成立时得到f(·)函数的极小值,则有λ=0,这样才能将拉格朗日函数直接转换为原始函数。则有λg(x,y)=0。
- 如果等式成立时得到f(·)函数的约束条件极小值,则必然存在λ>O,且同时g(x,y)=0,因此也有λg(x,y)=0。
于是,对于不等式约束条件g(x,y)≤0,最终的约束条件变成了:
- g(x, y)≤0
- λ≥0
- λg(x, y)=0
这样由一变三的约束条件,叫作 KKT 约束条件
12.3 对偶学习算法
12.3.1 对偶问题
主问题
我们考虑在d维空间上有m个等式约束条件和n个不等式约束条件的极小化问题
其中x为d维
我们把上述问题称为主问题
为了解决主问题,我们引入拉格朗日乘子λ和μ,并构造拉格朗日函数为
再设
其中D为主问题的可行域,且
当μ非负时
假设x^是主问题可行域的一点
假设主问题的最优解为p*,则
因此,Γ(λ,μ)是主问题最优解的下界
我们称
为主问题的对偶问题,λ,μ称为对偶变量
12.3.2 强对偶性
设对偶问题的最优解为d*,显然有d*≤p*。若d*==p*,则我们将主问题和对偶问题的关系称为强对偶性,否则称为弱对偶性。显然,强对偶性如果成立,我们就可以通过最优化对偶问题来达到最优化主问题的目的了。
那么什么时候强对偶性成立呢?
如果主问题是凸优化问题,那么当下面3个条件同时成立时,强对偶性成立。
- 拉格朗日函数中的f(x)和g(x)都是凸函数
- h(x)是仿射函数;
- 主问题可行域中至少有一点使得不等式约束严格成立。即存在x,对所有j,均有g(x)<0
12.4 求解线性可分SVM的目标函数
12.4.1 线性可分SVM的主问题
其中α为拉格朗日乘子
其显然满足强对偶的三个条件
因此,线性可分SVM的目标函数可以通过求解其对偶问题来求解
12.4.2 使用对偶算法求解线性可分SVM的步骤
步骤1:对主问题构造拉格朗日函数
步骤2:求拉格朗日对于w和b的极小
分别对w和b求偏导,令偏导为零,得到
带入拉格朗日函数,得到
步骤3:求对α的极大
由
得到
步骤4:求解α
设最优解为α*
这是一个典型的二次规划问题,可以使用二次规划方法求解
但为了节约开销,我们采用SMO算法求解
为了大致理解,可以参考
SMO算法最通俗易懂的解释_Y1ran_的博客-CSDN博客_smo算法
这里略去
假设我们已经求解出α*
步骤5:由α*求w
代入下面式子即可
步骤6:由w求b
注意这里求的是均值
步骤7:最终结果
构造最大分割超平面
利用符号函数构造分类决策函数
12.5 线性SVM,间隔由硬到软
12.5.1 线性SVM的主问题
引入松弛变量ξ,如图所示
因此,线性SVM的主问题为
12.5.2 求解过程
第一步,构建拉格朗日函数
第二步,极大极小化拉格朗日函数
分别对三个主问题参数求偏导,得到
代回对偶问题中,得到
然后对α和μ极大化
这和线性可分最优化过程的极小化目标是一样的,只是约束条件不同。
我们同样可以使用SMO算法
12.6.3 线性SVM的支持向量
我们先来看看线性SVM的主问题的KKT条件
我们还知道
因此,α为0的项对w的值是没有影响的
由KKT条件的第三行,可知,能够影响w的样本,一定满足
下面针对ξ,分三种情况讨论
ξ=0,则此时样本刚好落在两个辅助超平面上
ξ≤1,此时虽然yf(x)不为1,但至少没有被归类错误
ξ>1,此时归错类了,但即便如此,也影响了w的取值
因此,对于线性SVM而言,除了落在两个辅助超平面上的样本,落在软间隔之间的样本也是支持向量
12.6 非线性SVM和核函数
12.6.1 非线性SVM
对于在有限维度向量空间中线性不可分的样本,我们将其映射到更高维度的向量空间中,再通过间隔最大化的方式,学习得到 SVM,就是非线性 SVM。
我们将样本映射到的更高维度的新空间叫作特征空间。
如果是理想状态,样本从原始空间映射到特征空间后直接就成为线性可分了,那么接下来的学习是可以通过硬间隔最大化的方式来学的。
不过,一般的情况总没有那么理想,因此在通常情况下,我们还是按照软间隔最大化的方式在特征空间中学习 SVM。
简单理解就是:非线性 SVM = 核技巧 +线性 SVM
我们用向量x表示位于原始空间中的样本,φ(x)表示x映射到特征空间之后的新向量
则非线性SVM的分隔超平面为
套用线性SVM的对偶问题,得到非线性SVM的对偶问题为
12.6.2 核函数
对于有限维度的原始空间,一定存在更高维度的空间,使得前者中的样本映射到新空间后可分。
但是新空间(特征空间)的维度也许很大,甚至可能是无限维的
这样的话直接计算φ(x)的内积就会很困难,为了避免这样的情况,我们需要设置一个新的函数k
由此以来,对偶问题变成了
最大分隔超平面变成了
函数可以作为核函数的充要条件:
半正定的对称矩阵
核函数的种类有哪些?
- 线性核:无需指定参数,直接计算两个输入向量的内积。经过线性核函数转换的样本,特征空间与输入空间重合,相当于并没有将样本映射到更高维度的空间里去。浙大胡浩基老师是这样描述线性核的“只具有理论的意义,没有实用价值”
- 多项式核:复杂度可以调节。指数d越大,对应的φ维度越高。这是一个不平稳的核,适用于对数据进行归一化的情况
- RBF核:参数设置非常关键。如果设置过大,则整个RBF 核会向线性核方向退化,向更高维度非线性投影的能力就会减弱;但如果设置过小,则会使得样本中噪声的影响加大,从而干扰最终SVM 的有效性。对应的φ维度是无限的。最常用的核函数
- Sigmoid核:β和b都是超参数。在某些参数设置之下,Sigmoid核矩阵可能不是半正定的,此时 Sigmoid核也就不是有效的核函数了。因此参数设置要非常小心。对应的φ维度是无限的
自定义核函数:
- 与正数相乘:k是核函数,对于任意正数(标量)a≥0,a*k也是核函数
- 与正数相加:k是核函数,对于任意正数(标量)a≥0,a+k也是核函数
- 线性组合:k是核函数,则其线性组合也是核函数:∑ak,α≥0
- 乘积:k1和k2都是核函数,则它们的乘积k1k2也是核函数
- 正系数多项式函数:设P为实数域内的正系数多项式函数,k是核函数,则P(k)也是核函数
- 指数函数:k是核函数,则exp(k)也是核函数
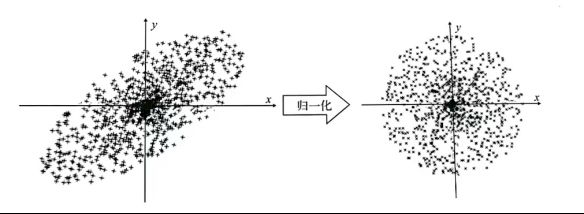
12.6.3 数据归一化
常用的归一化算法有两种
- 最大-最小归一化
- 平均归一化
第13章 SVR
13.1 宽容的SVR
13.1.1 模型函数
SVR模型的模型函数也是一个线性函数:y=wx+b
它看起来和线性回归的模型函数一样,但 SVR 和线性回归是两个不同的回归模型:
- 计算损失的原则不同
- 目标函数和最优化算法不同
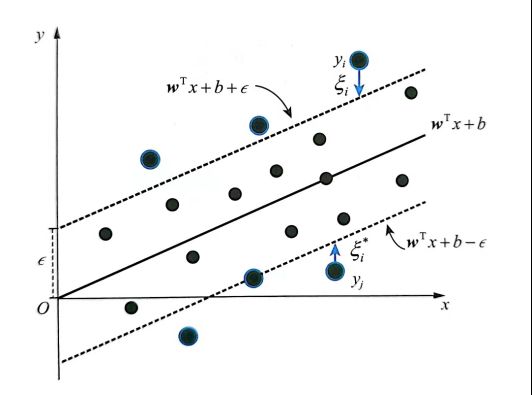
13.1.2 原理
SVR在线性函数两侧制造了一个“隔离带”, 对于所有落入隔离带的样本,都不计算损失,只有隔离带之外的,才计入损失函数。之后再通过最小化隔离带的宽度与总损失,来最优化模型。如图所示
13.1.3 两个松弛变量
SVR和SVM有很多相似之处。但SVR 有一点和SVM相反:SVR希望所有的样本点都落在隔离带里面,而SVM恰恰希望所有的样本点都落在隔离带之外。正是这一点区别,导致SVR要同时引入2个而不是1个松弛变量
13.2 SVR的主问题和对偶问题
SVR主问题的数学描述如下
引入拉格朗日乘子μ、μ*、α、α*
得到拉格朗日函数如下
与之对应的对偶问题是
先求其最小化部分。
分别对w、b、ξ、ξ*求偏导,并令偏导数为0,得到
代回对偶问题中,得到
此时由于存在α、α*两个参数,无法直接使用SMO算法
我们先来看看SVR对偶问题的KKT条件
显然α、α*其中至少有一个为0
设λ=α-α*
则|λ|=α+α*
代回对偶问题,得到
如此以来,就可以使用SMO求解了
13.3 支持向量与求解线性模型参数
之前在求偏导时我们得到
因此
由此可见,只有α≠α*的样本才对w的取值有意义,才是SVR的支持向量
结合KKT条件,显然落在隔离带之外的向量才是SVR的支持向量
其中Su是位于隔离带上边缘的支持向量集合,Sd是位于隔离带下边缘的支持向量集合