Coursera-吴恩达机器学习课程个人笔记-Week7

1.支持向量机(SVM,Support Vector Machine)的数学表达

  本章中的向量和矩阵不再加粗，请读者自行判断，如有疑问可以留言咨询。

1.1从逻辑回归过渡到SVM

  从另一角度分析逻辑回归的sigmoid函数。对于二分类问题，我们希望的是
$$如果y=1,那么h_{\theta }(\text{x})\to 1，⟺{\text{θ}}^T\text{x}\gg 0$$
$$如果y=0,那么h_{\theta }(\text{x})\to 0，⟺{\text{θ}}^T\text{x}\ll 0$$
  那么，对于一个样本(x,y)来说，逻辑回归的损失函数为：
$$cost=-y\log h_{\theta }(x)-(1-y)\log (1-h_{\theta }(x))$$
$$=-y\log \frac{1}{1+e^{-{\text{θ}}^T\text{x}}}-(1-y)\log (1-\frac{1}{1+e^{-{\text{θ}}^T\text{x}}})$$
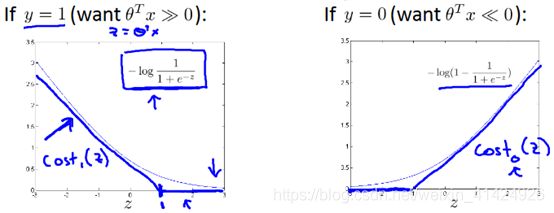  SVM是当y=1时，将$-\log \frac{1}{1+e^{-z}}$项替换为$cos{t}_1(z)$，其函数图像如上图左所示，由两条直线表示；同理当y=0时，用$cos{t}_0(z)$替代$-\log (1-\frac{1}{1+e^{-z}})$项，如上图右所示。其中，cost(z)函数由于像门的合叶，因此也叫Hinge损失函数。
   理论上，想要完全区分正负例，只需要${\theta }^{T}x>0$或${\theta }^{T}x<0$即可。但是SVM更加严格，为了表示出${\theta }^{T}x>>0$，所以$cos{t}_1(z)$是以(1,0)作为转折点，而不是(0,0)。$cos{t}_0(z)$同理。

1.2 SVM的损失函数

  经过1.1的变化后，可以得到SVM的损失函数表达式如下：
$$J(\theta )=C\sum _{i=1}^m[y^{(i)}cos{t}_1({\theta }^T{x}^{(i)})+(1-y^{(i)})cos{t}_0({\theta }^T{x}^{(i)})]+\frac{1}{2}\sum _{j=1}^n{\theta }_j^2$$
  其中，通常C=1/λ。作为对比，以下是逻辑回归的损失函数：
$$J(\theta )=-\frac{1}{m}\sum _{i=1}^m[y^{(i)}\log h(x^{(i)})+(1-y^{(i)})\log (1-h(x^{(i)}))]+\frac{\lambda }{2m}\sum _{j=1}^n{\theta }_j^2$$
  通常人们用支持向量机的时候，会把1/m这一项删去，没有特殊的原因，也不会影响最优参数的结果。另外，会在正则项的系数上做一些变化，把原先的超参数λ融入到超参数C中，并从第二项移到第一项。虽然数学本质相同，但是表达了两个损失函数正则化的侧重点不同：逻辑回归的正则化侧重点在于第二项的正则项，而SVM的侧重点在于第一项。

1.3 SVM的预测值

  和逻辑回归不同，SVM输出的不是预测值概率，而直接是类别，即：
$$h_{\theta }(x^{(i)})=\{\begin{array}{l}1,if{\theta }^T{x}^{(i)}\ge 0\\ 0,if{\theta }^T{x}^{(i)}<0)\end{array}$$

2. SVM的理解

  当C很大的时候会出现什么情况？(相当于正则项很小)
  这时根据SVM的损失函数可知，为了尽量减小损失值，又由于C很大，因此会思考使得第一项尽量为0，只留下第二项。要使第一项为零，需要满足如下条件：
$$\{\begin{array}{l}当y=1时，cos{t}_1({\theta }^T{x}^{(i)})=0,即{\theta }^T{x}^{(i)}\ge 1\\ 当y=0时，cos{t}_0({\theta }^T{x}^{(i)})=0,即{\theta }^T{x}^{(i)}\le -1\end{array}$$
  此时，损失值的优化问题就转换为：
$$\underset{\theta }{\min }\frac{1}{2}\sum _{j=1}^n{\theta }_j^2，s.t.\{\begin{array}{l}当y=1时，{\theta }^T{x}^{(i)}\ge 1\\ 当y=0时，{\theta }^T{x}^{(i)}\le -1\end{array}$$
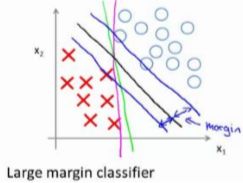  转化后的优化问题会在完全分割正负例的基础上(如上图的粉线、绿线和黑线)，找到上图黑线的分割线，使得正负例距离分割线最近的样本与分割线的距离最大，因此SVM也叫large margin classifier。图中，正负例距离分割线最近的样本与分割线的距离就称作间距(margin)。
  切记，上述情况是在超参数C很大的时候得到的。
  实际上，SVM的超参数通常设置的不会很大，也就使得SVM算法本身要比上述的large margin classifier更成熟。这体现在SVM对于离群样本等异常值的处理，比如下图：
  当C选很大时，最终可能得到的是图中粉色的分割线。而SVM中选择合适的C数值时，最终可以得到黑色分割线。很明显，黑色分割线是更符合实际的。
  因此，超参数C其实和逻辑回归的超参数λ类似，可以控制模型的泛化能力。但效果与λ正好相反。当C较大时，相当于λ较小，可能导致模型过拟合；当C较小时，相当于λ较大，可能导致模型欠拟合。

3. SVM的推导

  为什么SVM算法能找出间距最大的决策边界？

3.1 吴恩达课程的思路

  1).向量内积的几何说明
  假设两个向量$u⃗,v⃗$。
  向量内积$u⃗\cdot v⃗=p\cdot ||u⃗||$
  其中，p是向量v ⃗投影到向量u ⃗上的长度，是个标量。注意，此处p是由正负的，如果两个向量夹角大于90°，则p是负值，如下图。
  其实就是向量$u⃗$的范数，即长度，也是标量。
  2). SVM的决策边界
  如第2章中SVM的优化问题转换为：
$$\underset{\theta }{\min }\frac{1}{2}\sum _{j=1}^n{\theta }_j^2，s.t.\{\begin{array}{l}当y=1时，{\theta }^T{x}^{(i)}\ge 1\\ 当y=0时，{\theta }^T{x}^{(i)}\le -1\end{array}$$
  假设$\theta =({\theta }_0,{\theta }_1,{\theta }_2{)}^{\prime }$，令${\theta }_0=0$方便理解且不影响后续推导的正确性。此时有：
$$\underset{\theta }{\min }\frac{1}{2}\sum _{j=1}^n{\theta }_j^2=\frac{1}{2}(\sqrt{{\theta }_1^2+{\theta }_2^2}{)}^2=\frac{1}{2}||\theta |{|}^2等价于\underset{\theta }{\min }||\theta ||$$
  其中，限制条件s.t.又可以改写成：
$$s.t.\{\begin{array}{l}当y=1时，{\theta }^T{x}^{(i)}\ge 1\\ 当y=0时，{\theta }^T{x}^{(i)}\le -1\end{array}⟺\{\begin{array}{l}{p}^{(i)}\cdot ||\theta ||\ge 1\\ p^{(i)}\cdot ||\theta ||\le -1\end{array}$$

  其中，$p^{(i)}$是样本$x^{(i)}$投影到参数向量θ上的距离。此处需要注意，参数向量其实就是最终决策边界的法向向量，所以样本$x^{(i)}$投影到参数向量θ上的距离$p^{(i)}$，其实就是样本$x^{(i)}$和决策边界的距离。
  因为限制条件s.t.已经把决策边界控制在绝大部分正例在边界一侧，绝大部分负例在边界另一侧，因此对于负例来说，$p^{(i)}<0$(如下图)。所以上述限制条件其实可以统一写成：
$$p^{(i)}\cdot ||\theta ||\ge 1$$
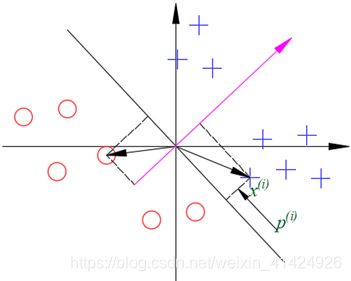  综上所述，SVM想要使得||θ||最小，那么，根据限制条件可知，等价于使得$p^{(i)}$最大，即样本点到决策边界的距离越大越好。因此，SVM算法能找出间距最大的决策边界。

3.2 更数学的SVM推导思路

  1).支持向量机原理的引论
  对于一般的直线：Ax+By+C=0，某点$(x_0,y_0)$到该直线的距离为：
$$d=\frac{|A{x}_0+B{y}_0+C|}{\sqrt{A^2+B^2}}$$
  其实$|A{x}_0+B{y}_0+C|=\pm (A{x}_0+B{y}_0+C)$，正负只是说明该点实在直线的正半区还是负半区，无实际数值意义，所以正负可以去掉，所以有：
$$d=\frac{A{x}_0}{\sqrt{A^2+B^2}}+\frac{B{y}_0}{\sqrt{A^2+B^2}}+\frac{C}{\sqrt{A^2+B^2}}$$
  上式可以看成向量的形式：
$$d=\left[\begin{array}{c}\frac{A}{\sqrt{A^2+B^2}}\\ \frac{B}{\sqrt{A^2+B^2}}\end{array}\right](x_0{y}_0)+\frac{C}{\sqrt{A^2+B^2}}$$
  令：
$$w{⃗}^T=\left[\begin{array}{c}A\\ B\end{array}\right],x=(x_0{x}_1=y_0),b=\frac{C}{\sqrt{A^2+B^2}},||w||=\sqrt{A^2+B^2}$$
$$\therefore d=\frac{1}{||w⃗||}w{⃗}^T\cdot x+b$$
  如果$\frac{1}{||w⃗||}w{⃗}^T$是归一化后的向量，$x⃗$是数据的特征组成的某样本点向量，那么$d=\frac{1}{||w⃗||}w{⃗}^T\cdot x{⃗}_1+b$表示的就是样本点$x{⃗}_1$到“直线$0=\frac{1}{||w⃗||}w{⃗}^T\cdot x+b$”的距离(正负表示正半区或负半区)。每个样本点都能求出一个距离值。所以我们需要找一条直线，使得最近的样本点距离该直线最远。即：
$$(w^{\ast },b^{\ast })=\arg \underset{w,b}{\max }\underset{i}{\min }(\frac{1}{||w⃗||}w{⃗}^T\cdot x{⃗}_i+b)$$
  推广到多维空间，所求的就是一个分割超平面。

  2).线性可分支持向量机
  记样本点数据为：
$$T=(x_1,y_1),(x_2,y_2),\dots ,(x_N,y_N)$$
  其中，$x_i\in R^n,y_i\in +1,-1,i=1,2,\dots ,N$；(若n>1则，x_i为向量)
称x_i为第i个实例，$y_i$为$x_i$的类标记，当$y_i=+1$时，称$x_i$为正例；反之$y_i=-1$时，称$x_i$为负例。(为什么这边要用±1？因为后边方便推导。当然也能多分类，只是用2分类推导作示例。另外，可以调高数值来调高正例或负例的权值，比如用-1和50，则说明正例权值调高。在样本不平衡时比较有效)
  给定线性可分的训练数据集，通过间隔最大化得到的分离超平面为：
$$0=\frac{1}{||w^{\ast }||}{w}^{\ast }\cdot \Phi (x)+b^{\ast }$$
  相应的分类决策函数：(即正为1，负为-1)
$$f(x)=sign(\frac{1}{||w^{\ast }||}{w}^{\ast }\cdot \Phi (x)+b^{\ast })$$
  该决策函数称为线性可分支持向量机。
  其中，Φ(x)是某个确定的特征空间转换函数，作用是将x映射到更高的维度，是已知量，即下文中的核函数。注意，下面推导里，$\Phi (x^{(i)})$都是个关于各种特征的向量。
  该问题等价于求解相应的凸二次规划问题。
  3).SVM目标函数的推导
  根据题设有
  令$y(x)=w{⃗}^T\cdot \Phi (x)+b$
$$\{\begin{array}{l}y(x^{(i)})>0\iff y^{(i)}=+1\\ y(x^{(i)})<0\iff y^{(i)}=-1\end{array}\iff y^{(i)}y(x^{(i)})>0$$
  w ⃗,b等比例缩放(相当于y=2x+1→y=4x+2)，则t*y的值同样缩放，从而：
$$\frac{y^{(i)}y(x^{(i)})}{||w||}=\frac{y^{(i)}\cdot (w^T\cdot \Phi (x^{(i)})+b)}{||w||}>0$$
  其中，|(|w ⃗ |)|=√(w_1^2+w_22+⋯)，除以||w ⃗||是对w ⃗进行归一化，所以((w ⃗^T·Φ(x_i)+b))/(||w ⃗|| )项就代表样本点到超平面的距离。
  所以目标函数就是求解使得距离超平面最近样本的间隔最大的分离超平面：
$$\arg \underset{w,b}{\max }\frac{1}{||w||}\underset{i}{\min }[y^{(i)}\cdot (w^T\cdot \Phi (x^{(i)})+b)]$$
  通过w ⃗,b等比例缩放，总能够使得min┬i⁡[(w ⃗^T·Φ(x((i)))+b)]=1，即样本点距离分割平面的最小距离为1。所以有如下不等式：
$$\forall i,|y^{(i)}|=|y^{(i)}\cdot (w^T\cdot \Phi (x^{(i)})+b)|\ge 1$$
  由于上述不等式的等号是可取的(当选取距离分割平面最近的样本点时取得)，所以目标函数转变为：
$$\arg \underset{w,b}{\max }\frac{1}{||w⃗||}\underset{i}{\min }[y^{(i)}\cdot (w{⃗}^T\cdot \Phi (x^{(i)})+b)]\Rightarrow \arg \underset{w,b}{\max }\frac{1}{||w⃗||}$$
  $\frac{1}{||w⃗||}$求最大值其实就是$||w⃗||$求最小值。因为$||w⃗||$有根号，所以再将$||w⃗||$取平方加系数0.5，即可得到最后的目标函数：
$$\arg \underset{w,b}{\max }\frac{1}{||w||}\Rightarrow \arg \underset{w,b}{\min }\frac{1}{2}||w|{|}^2$$
$$s.t.(约束条件)：\forall i,|y^{(i)}|=|y^{(i)}\cdot (w^T\cdot \Phi (x_i)+b)|\ge 1$$
  仔细观察可以发现，两者的解释角度虽然不太一样，但是最终的结果是一致的。吴恩达的思路更容易理解，是从直观角度进行解释；而邹博的解释比较理论，是从数学角度进行解释。
  4).SVM目标函数优化问题的求解(拓展)
  有时间再加上。

4.核函数(kernels)

4.1定义

  核函数是某个确定的特征空间转换函数，作用是将x映射到其他维度。
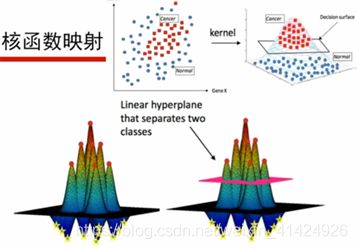  如上图，通过高斯核函数，就将二维平面的样本集，映射到高维空间，使得样本原来线性不可分，转换为了线性可分。
  核函数举例：
  给定一组训练实例x，利用x的各个特征和我们预先选定的地标(landmarks) $l^{(1)},l^{(2)},l^{(3)}$的相似度(similarity)作为新的特征$f_1,f_2,f_3$。如下图所示：

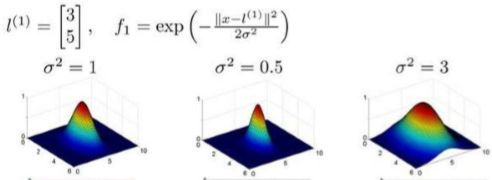
$$f_i=similarity(x,l^{(i)})=exp(\frac{-||x-l^{(i)}|{|}^2}{2{\sigma }^2})$$
  其中，$||x-l^{(i)}|{|}^2={\sum }_{j=1}^n(x_j-l_j^{(i)}{)}^2$，是样本x中所有特征与地标$l^{(i)}$之间的距离之和。此处$k(x,l^{(i)})=similarity(x,l^{(i)})$就是高斯核函数，是核函数的一种。

4.2地标的作用是什么？

  如果样本x与地标$l^{(i)}$之间的距离近似于0，则新特征$f_i\to 1$；反之，如果距离较远，则新特征$f_i\to 0$。所以可以看出，新特征与地标的位置关系十分密切。
  另外高斯核函数中的超参数σ控制了特征的泛性，σ越大，则特征的泛性越大，如下图。
  通过设置地标，可以看到下图中，当θ=(-0.5,1,1,0)时，大概处于红色范围内的区域，预测值$h_{\theta }(x)=1$。而其他区域，预测值$h_{\theta }(x)=0$。所以，可以看出，地标基本上构建了一个非线性的决策边界。

4.3地标(Landmark)怎么选择？

  通常是根据训练集的数据选择地标。如果训练集有m个样本，那么就选择m个地标，并且有$l^{(i)}=x^{(i)}$,i=1,2,…,m。注意，新特征$f=[f_0,f_1,\dots ,f_m]$中，通常也包含$f_0=1$这一特征。

4.4 核函数种类(拓展)

  1).多项式核函数
$$k(x,l)=(\alpha \cdot \Vert x-l{\Vert }^a+r{)}^b，\alpha ,a,b,r为常数$$
  2).高斯核函数RBF
$$k(x,l)=exp(\frac{-\Vert x-l{\Vert }^2}{2{\sigma }^2})，\sigma 是超参数$$
  3).Sigmoid核函数
$$k(x,l)=tanh(\gamma \cdot \Vert x-l{\Vert }^a+r)，\gamma ,a,r为常数$$
  核函数的选择：
  1).如果有先验知识，知道要用哪种核函数，那就用该核函数；
  2).如果数据够多，可以用实验的方式，交叉验证，选择效果最好的核函数；
  3).如果没有任何先验知识，那就使用高斯核函数。(因为高斯核可以说是把数据映射到无穷维的空间，所以区分度就很强。但是也要注意过拟合问题。)

  理论上，核函数也可以用在逻辑回归等地方，但是由于数学表达式不同，其他算法用核函数的计算量会很大，而SVM的算法中，刚好可以对核函数的计算做一点点改善，而大大提高算法效率(具体方法查阅数学理论)。所以通常核函数这种方法是用在SVM中。
  也不是所有函数都能用作核函数，通常核函数需要满足“Mercer‘s Theorem”,才可以使核函数在优化计算中大大加速且保证收敛，否则，不满足条件的函数加入SVM后效率非常低，甚至会发散。

5.SVM的应用

5.1 SVM和核函数的结合

  1).给定样本集$x^{(i)}$,使用核函数计算新特征样本集$f^{(i)}=k(x^{(i)},l^{(i)})$；
  注意，在使用高斯核函数前，必须做一下特征的缩放，因为特征值的范围通常非常不同。
  2).将修改后的样本集代入SVM的损失函数进行优化计算：
$$J(\theta )=C\sum _{i=1}^m[y^{(i)}cos{t}_1({\theta }^T{f}^{(i)})+(1-y^{(i)})cos{t}_0({\theta }^T{f}^{(i)})]+\frac{1}{2}\sum _{j=1}^{n(n=m)}{\theta }_j^2$$
  实际使用时，在计算∑_(j=1)^{(n(n=m))▒θ_j}2 =θ^T θ时，其实是计算了θ^T Mθ，M矩阵的选择是根据核函数而定的，这样做可以大大加快计算速度，原理这里不介绍了。所以，通常SVM的最优参数的求解是利用已有函数库来解决。
  3). SVM主要调参超参数是两个，一个是C，一个是核函数的σ。
  C较大时，相当于λ较小，可能会导致过拟合，高方差；
  C较小时，相当于λ较大，可能会导致欠拟合，高偏差；
  σ较大时，可能会导致欠拟合，高偏差；
  σ较小时，可能会导致过拟合，高方差；

5.2 多分类SVM

  类似于逻辑回归的one vs all方法。

5.3 SVR(Support Vector Regression)

  SVM处理回归问题，即SVR。有时间再补充。

5.4 SVM的一些注意点

  1).不使用任何核函数，也叫做使用“线性核函数”；
  2).如果当n≫m时(eg:n=10000+,m=10~1000)，即特征数量远大于样本数量，会使用逻辑回归或者不使用核函数的SVM，因为特征数量太大，核函数的使用会明显影响算法效率；
  3).如果n较小，且m适中(eg:n=1~1000, m=10~10000)，使用高斯核函数的SVM；
  4).如果m≫n(eg:n=1~1000,m=50000+)，要么增加样本特征，要么使用逻辑回归或者不使用核函数的SVM，不用核函数是因为算法效率会大大下降；
  5). SVM是个凸优化过程，所以不用担心寻找到的是局部最优解。