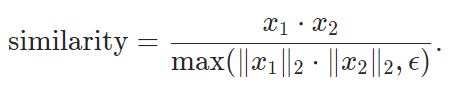pytorch一行实现：计算同一tensor矩阵内每行之间的余弦相似度

0 输入数据

import torch
# 设置随机数种子，以保证结果可重现
torch.manual_seed(0)
a = torch.randn(4, 3)

tensor([[ 1.5410, -0.2934, -2.1788],
        [ 0.5684, -1.0845, -1.3986],
        [ 0.4033,  0.8380, -0.7193],
        [-0.4033, -0.5966,  0.1820]])

1 余弦相似度（Cosine Similarity）

  余弦相似度的公式如下所示：

2 torch.cosine_similarity

  可以使用torch自带的余弦相似度计算函数（下面三种用哪一个都可以，效果是一样的）：

torch.cosine_similarity(x1, x2, dim=1, eps=1e-08)
torch.nn.CosineSimilarity(x1, x2, dim=1, eps=1e-08)
torch.nn.functional.cosine_similarity(x1, x2, dim=1, eps=1e-08) → Tensor

  该函数原文档在：torch官方文档

3 问题

  cosine_similarity中的参数要两个tensor数据，而我们的需求是求一个tensor内的行与行之间的余弦相似度。很显然不能直接使用该函数。

4 分析与解决

  变量a的shape是(4, 3), 求a中的行与行之间的相似性，每行与每行有一个相似度，那么最终得到的结果应该是shape为(4, 4)。这个结果意味着a中的每一行要与包括本行在内的4行都有一个相似度数值。
  如下图所示，以第一行与所有行的相似度计算为例：

  分别拿着第一行的数据再与右侧所有行的数据按照余弦相似度计算，然后再换第二行的数据再与右侧所有行数据计算。这是正常人类的计算过程。
  固然上图中的处理torch 配合for循环依然能够实现。但是torch的一种快捷做法如下图所示，直接将第一行数据复制多份，每一份分别与右侧的每一行计算。

  按照这个逻辑，下图则是计算的全过程：

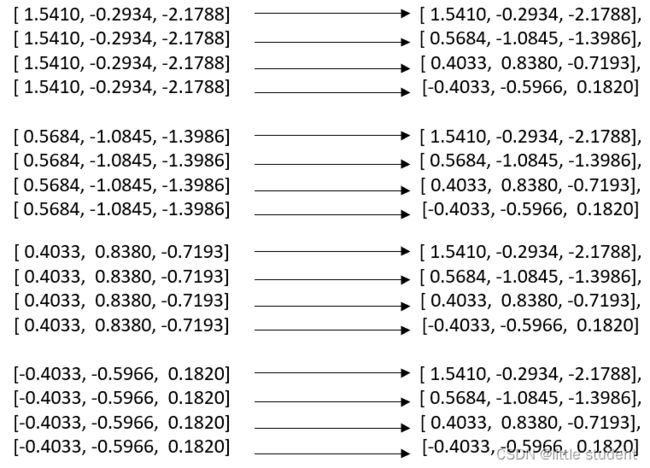
  如此就满足torch.cosine_similarity需要输入两个tensor的要求了。左侧的数据是每一行都分别复制了4次，右侧的是整体所有行被复制了4次。

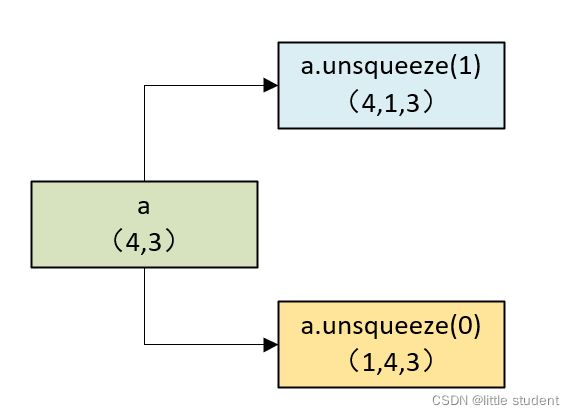
  a.unsqueeze(1)得到一个shape为(4,1,3)的tensor，a.unsqueeze(0)得到一个shape为(1,4,3)的tensor。（4，1，3）的tensor要和（1，4，3）的tensor进行运算，必须扩充到同一个shape，这样就都变成了(4，4，3),这就是torch的广播机制(broadcast)。
  而在广播过程中，shape为(4,1,3)的tensor要变成(4,4,3)的tensor就只能把后边的3多复制几次。也就实现了上图中的左侧tensor的效果；同理shape为(1,4,3)的tensor要变成(4,4,3)的tensor就只能把后边的(4,3)多复制几次。

4.1 答案

  因此对于一个shape为(4,3)的tensor，使用下行公式可以得到其行与行的余弦相似度。

similarity = torch.cosine_similarity(a.unsqueeze(1), a.unsqueeze(0), dim=-1)

tensor([[ 1.0000,  0.8499,  0.6155, -0.4228],
        [ 0.8499,  1.0000,  0.1493,  0.1182],
        [ 0.6155,  0.1493,  1.0000, -0.9087],
        [-0.4228,  0.1182, -0.9087,  1.0000]])

5 另外的实现方法

  上述是一行实现余弦相似度的代码，在代码角度上非常简洁，但是会消耗较多的时间（因为参与计算的维度增大的原因）。下面可以根据公式两行代码实现，由公式可以看出，两行之间的余弦相似度是通过方差归一化后的两行数值内积得到的。
所以方法如下：

a = a / torch.norm(a, dim=-1, keepdim=True) # 方差归一化，即除以各自的模
similarity = torch.mm(a, a.T) # 矩阵乘法

  该方法可以不通过扩充快速实现同一tensor矩阵内每行之间的余弦相似度。该方法在CPU上的求解速度几乎是torch.cosine_similarity的10X倍。

如果该内容对您有用，请点击 收藏+点赞