机器学习算法学习笔记：朴素贝叶斯

一、理论篇

1、概述

朴素贝叶斯（naive Bayes）算法是有监督的学习算法，解决的是分类问题，如客户是否流失、是否值得投资、信用等级评定等多分类问题。该算法的优点在于简单易懂、学习效率高、在某些领域的分类问题中能够与决策树、神经网络相媲美。但由于该算法以自变量之间的独立（条件特征独立）性和连续变量的正态性假设为前提，就会导致算法精度在某种程度上受影响。

朴素贝叶斯法是基于贝叶斯定理与特征条件独立假设的分类方法。对于给定的训练数据集，首先基于特征条件独立假设学习输入输出的联合概率分布；然后基于此模型，对给定的输入$x$，利用贝叶斯定理求出后验概率最大的输出$y$。朴素贝叶斯法实现简单，学习与预测的效率都很高，是一种常用的方法。

2、频率学派与贝叶斯派

在说极大似然估计（MLE）与最大后验概率估计（MAP）之前，不得不说对于概率看法不同的两大派别频率派与贝叶斯派。他们看待世界的视角不同，导致他们对于产生数据的模型参数的理解也不同。

（1）频率派：

他们认为世界是确定的。他们直接为事件本身建模，也就是说事件在多次重复实验中趋于一个稳定的值$p$，那么这个值就是该事件的概率。

他们认为模型参数是个定值，希望通过类似解方程组的方式从数据中求得该未知数。这就是频率派使用的参数估计方法-极大似然估计（MLE），这种方法往往在大数据量的情况下可以很好的还原模型的真实情况。

（2） 贝叶斯派

他们认为世界是不确定的，因获取的信息不同而异。假设对世界先有一个预先的估计，然后通过获取的信息来不断调整之前的预估计。 他们不试图对事件本身进行建模，而是从旁观者的角度来说。因此对于同一个事件，不同的人掌握的先验不同的话，那么他们所认为的事件状态也会不同。

他们认为模型参数源自某种潜在分布，希望从数据中推知该分布。对于数据的观测方式不同或者假设不同，那么推知的该参数也会因此而存在差异。这就是贝叶斯派视角下用来估计参数的常用方法-最大后验概率估计（MAP），这种方法在先验假设比较靠谱的情况下效果显著，随着数据量的增加，先验假设对于模型参数的主导作用会逐渐削弱，相反真实的数据样例会大大占据有利地位。极端情况下，比如把先验假设去掉，或者假设先验满足均匀分布的话，那它和极大似然估计就如出一辙了。

3、极大似然估计与最大后验概率估计

如果我们现在有一个任务，就是根据已知的一堆数据样本，来推测产生该数据的模型的参数，即已知数据，推测模型和参数。因此根据两大派别的不同，对于模型的参数估计方法也有两类：极大似然估计与最大后验概率估计。

（1）极大似然估计（MLE）-频率派模型参数估计的常用方法。

似然，可以简单理解为概率、可能性，也就是说要最大化该事件发生的可能性。它的含义是根据已知样本，希望通过调整模型参数来使得模型能够最大化样本情况出现的概率。

• 例子：假如一个盒子里面有红黑共10个球，每次有放回的取出，取了10次，结果为7次黑球，3次红球。问拿出黑球的概率$p$是多少？

我们假设7次黑球，3次红球为事件 A ，一个理所当然的想法就是既然事件 A已经发生了，那么事件 A 发生的概率应该最大。所以既然事件 A 的结果已定， 我们就有理由相信这不是一个偶然发生的事件，这个已发生的事件肯定一定程度上反映了黑球在整体中的比例。所以我们要让模型产生这个整体事件的概率最大，我们把这十次抽取看成一个整体事件 A ，很明显事件 A 发生的概率是每个子事件概率之积。我们把$P(A)$ 看成一个关于$p$的函数，求$P(A)$ 看取最大值时的$p$，这就是极大似然估计的思想。具体公式化描述为$P(A)=C_{10}^7{p}^7(1-p{)}^3$。

接下来就是取对数$ln$转换为累加，然后通过求导令式子为0来求极值，求出$p$的结果。

取对数得：（对数似然）$$L(p)=ln(P(A))=ln(p^7(1-p{)}^3)=7ln(p)+3ln(1-p)$$

$$p=\underset{p}{\mathrm{argmax}}L(p)$$

令$L^{\prime }(p)=0$，得$$\frac{7}{p}+\frac{3}{p-1}=0$$

解得$p=0.7$。

贝叶斯分类器的训练过程就是参数估计。总结最大似然法估计参数的过程，一般分为以下四个步骤：
①写出似然函数；
②对似然函数取对数，并整理；
③求导数，令偏导数为0，得到似然方程组；
④解似然方程组，得到所有参数即为所求。

【数值下溢问题：是指计算机浮点数计算的结果小于可以表示的最小数，因为计算机的能力有限，当数值小于一定数时，其无法精确保存，会造成数值的精度丢失，由上述公式可以看到，求概率时多个概率值相乘，得到的结果往往非常小；因此通常采用取对数的方式，将连乘转化为连加，以避免数值下溢】

（2）最大后验概率估计（MAP）-贝叶斯派模型参数估计的常用方法。

根据已知样本，来通过调整模型参数使得模型能够产生该数据样本的概率（后验概率）最大，只不过对于模型参数有了一个先验假设，即模型参数可能满足某种分布，不再一味地依赖数据样例（万一数据量少或者数据不靠谱呢）。

• 例子：抛一枚硬币10次，有10次正面朝上，0次反面朝上。求正面朝上的概率$p$。

在频率派看来，利用极大似然估计可以得到$p=10/10=1$。显然当缺乏数据时MLE可能会产生严重的偏差。

如果我们利用极大后验概率估计来看这件事，先验认为大概率下这个硬币是均匀的（例如最大值取在0.5处的Beta分布），那么$P(p|X)$是一个分布，最大值会介于0.5~1之间，而不是武断的给出$p=1$。

4、判别式模型和生成式模型

首先我们需要明确，两种不同的模型都用于监督学习任务中。监督学习的任务就是从数据中学习一个模型，并用基于这个模型对给定的输入预测相应的输出。这种模型的一般形式为决策函数$y=f(x)$或者条件概率分布$P(y|x)$。

生成式模型先对数据的联合分布$P(x,y)$进行建模，然后再通过贝叶斯公式计算样本属于各类别的后验概率$P(y|x)=\frac{P(x,y)}{P(x)}$。

判别式模型直接进行条件概率建模，由数据直接学习决策函数$y=f(x)$或条件概率分布$P(y|x)$作为预测的模型。判别方法不关心背后的数据分布，关心的是对于给定的输入，应该预测什么样的输出。

【用一句话总结就是生成模型估计的是联合概率分布，判别式模型估计的是条件概率分布】

• 例子1：两种模型来如何确定一只羊是山羊还是绵羊？

生成式模型：首先根据山羊的数据和绵羊的数据分别学习出山羊的特征$p(x,y_1)$和绵羊的特征$p(x,y_2)$，然后从待识别的羊中提取特征$x$，将这些特征分别放到山羊模型和绵羊模型中并得到条件概率$p(y_1|x)=\frac{p(x,y_1)}{p(x)}$和$p(y_2|x)=\frac{p(x,y_2)}{p(x)}$，如果$p(y_1|x)>p(y_2|x)$，那么我就认为这只羊属于山羊，否则为绵羊。

判别式模型：直接从山羊和绵羊的数据中提取特征$x$并学习得到模型$f(x)$，然后从待识别的羊中提取特征$x$，然后带入到模型中以判断这只羊是绵羊和山羊概率（比如 LR 中，结果大于 0.5 为正例，小于 0.5 为反例）。

我们可以看到，生成式模型强调数据本身特点，判别式模型强调数据边界。在分类的过程中，生成式模型对每个结果都要亲自试一试，遍历完一遍后取概率最大的结果；而判别式模型直接通过模型得到结果。

• 例子2：对于给定数据集$(x,y)$：(1,0),(1,1),(1,1),(2,0),(2,0),(2,1)。

生成式模型 $p(x,y)$：

如果现在有一个$x=2$，那我们可以得到：
$$P(y=0|x=2)=\frac{p(y=0,x=2)}{p(x=2)}=\frac{2}{3}$$
$$P(y=1|x=2)=\frac{p(y=1,x=2)}{p(x=2)}=\frac{1}{3}$$

判别式模型$p(y|x)$：

对于给定的$x=2$，我们直接可以得到$P(y=1|x=2)$和$P(y=0|x=2)$的值。

【特点】

生成式模型的特点在于，其可以从统计的角度表示数据的分布情况，能反映同类数据本身的相似度，不关心各类的边界在哪；
而判别式模型直接学习的是条件概率分布，所以其不能反映训练数据本身的特性，其目的在于寻找不同类别之间的最优分界面，反映异类数据之间的差异。
由生成模型可以得到判别模型，但由判别模型得不到生成模型。
当存在隐变量（当我们找不到引起某一现象的原因的时候，我们就把这个在起作用但是无法确定的因素，叫“隐变量”） 时，仍可以利用生成方法学习，此时判别方法不能用。因为生成式模型同时对$x$和$y$建立概率模型，所以如果$x$中有出现没有观察到的量或者只有部分$y$的时候，就可以很自然地使用 EM 算法 来进行处理。极端情况下，在完全没有 $y$信息的情况下，GM 仍然是可以工作的——无监督学习可以看成是 GM 的一种。

【优缺点】

（1）生成式模型 ：

• 优点
  ①由于统计了数据的分布情况，所以其实际带的信息要比判别模型丰富，对于研究单类问题来说也比判别模型灵活性强；
  ②模型可以通过增量学习得到（增量学习是指一个学习系统能不断地从新样本中学习新的知识，并能保存大部分以前已经学习到的知识）；
  ③收敛速度更快，当样本容量增加的时，生成模型可以更快的收敛于真实模型；
  ④隐变量存在时，也可以使用。

• 缺点
  ①学习和计算过程比较复杂，由于学习了更多的样本信息，所以计算量大，如果我们只是做分类，就浪费了这部分的计算量；
  ②准确率较差；
  ③往往需要对特征进行假设，比如朴素贝叶斯中需要假设特征间独立同分布，所以如果所选特征不满足这个条件，将极大影响生成式模型的性能。

（2）判别式模型 ：

• 优点
  ①由于关注的是数据的边界，所以能清晰的分辨出多类或某一类与其他类之间的差异，所以准确率相对较高；
  ②计算量较小，需要的样本数量也较小；

• 缺点
  ①不能反映训练数据本身的特性；
  ②收敛速度较慢。

【代表算法】
生成式模型：朴素贝叶斯、贝叶斯网络、隐马尔可夫模型、隐马尔可夫模型；
判别式模型：k 近邻法、决策树、逻辑斯谛回归模型、最大熵模型、支持向量机、条件随机场。

5、贝叶斯定理

不管是在投资领域，还是机器学习，或是日常生活中，几乎都在用到贝叶斯定理。生命科学家用贝叶斯定理研究基因是如何被控制的；教育学家突然意识到，学生的学习过程其实就是贝叶斯法则的运用；基金经理用贝叶斯法则找到投资策略；Google用贝叶斯定理改进搜索功能，帮助用户过滤垃圾邮件；无人驾驶汽车接收车顶传感器收集到的路况和交通数据，运用贝叶斯定理更新从地图上获得的信息；人工智能、机器翻译中大量用到贝叶斯定理。

5.1 贝叶斯定理有什么用

【例子】一个抽奖箱子里有10个球，其中2个白球，8个黑球，抽到白球就算你中奖。你伸手进去随便摸出1颗球，摸出中奖球的概率是多大？

根据频率概率的计算公式，你可以轻松的知道中奖的概率是2/10。

以上的问题其实是属于一个“正概率”问题。而贝叶斯定理的提出是为了解决一个“逆概率”问题。比如上面的例子我们并不知道抽奖箱子里有什么，而是摸出一个球，通过观察这个球的颜色，来预测这个箱子里里白色球和黑色球的比例。

这个预测其实就可以用贝叶斯定理来做。

贝叶斯定理席卷了概率论，并将应用延伸到各个问题领域。可以说，所有需要作出概率预测的地方都可以见到贝叶斯定理的影子，贝叶斯是机器学习的核心方法之一。例如垃圾邮件过滤，中文分词，艾滋病检查，肝癌检查等。

为什么贝叶斯定理在现实生活中这么有用呢？
这是因为现实生活中的问题，大部分都是像上面的“逆概率”问题。生活中绝大多数决策面临的信息都是不全的，我们手中只有有限的信息。既然无法得到全面的信息，我们就在信息有限的情况下，尽可能做出一个好的预测。

在现实世界中，我们每个人都需要预测。想要深入分析未来、思考是否买股票、政策给自己带来哪些机遇、提出新产品构想，或者只是计划一周的饭菜。

贝叶斯定理就是为了解决这些问题而诞生的，它可以根据过去的数据来预测出概率。贝叶斯定理的思考方式为我们提供了明显有效的方法来帮助我们提供能力，以便更好地预测未来的商业、金融、以及日常生活。

5.2 什么是贝叶斯定理

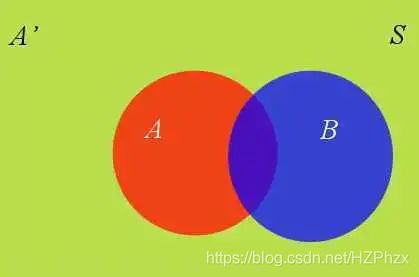
条件概率公式：（在B条件下发生A的概率）
$$P(A|B)=\frac{P(AB)}{P(B)}$$
乘法公式：$$P(AB)=P(A|B)P(B)=P(B|A)P(A)$$
全概率公式：$$P(B)=P(B|A)P(A)+P(B|A^{\prime })P(A^{\prime })$$
贝叶斯公式：（乘法公式/全概率公式）
$$P(A|B)=\frac{P(AB)}{P(B)}=P(A)\frac{P(B|A)}{P(B)}$$

• 例子：小鹿说，他的女神每次看到他的时候都冲他笑，他想知道女神是不是喜欢他呢？

下面我们一起用贝叶斯帮小鹿预测下女神喜欢他的概率有多大，这样小鹿就可以根据概率的大小来决定是否要表白女神。

首先，我分析了给定的已知信息和未知信息：
1）要求解的问题：女神喜欢你，记为A事件；
2）已知条件：女神经常冲你笑，记为B事件。

所以说，$P(A|B)$是女神经常冲你笑这个事件（B）发生后，女神喜欢你（A）的概率。

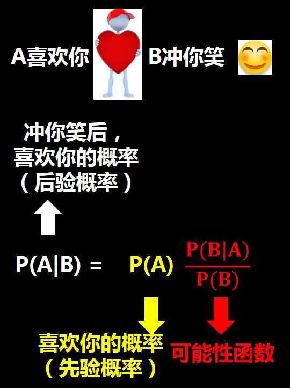
从公式来看，我们需要知道这么3个事情：

1）先验概率

我 们把$P(A)$称为“先验概率”，即在不知道B事件的前提下，我们对A事件概率的一个主观判断。这个例子里就是在不知道女神经常对你笑的前提下，来主观判断出女神喜欢一个人的概率，这里我们假设是50%，也就是不能喜欢你，可能不喜欢还你的概率都是一半。

2）可能性函数

$P(B|A)/P(B)$称为“可能性函数”，这是一个调整因子，即新信息B带来的调整，作用是使得先验概率更接近真实概率。

可能性函数你可以理解为新信息过来后，对先验概率的一个调整。比如我们刚开始看到“人工智能”这个信息，你有自己的理解（先验概率/主观判断），但是当你学习了一些数据分析，或者看了些这方面的书后（新的信息），然后你根据掌握的最新信息优化了自己之前的理解（可能性函数/调整因子），最后重新理解了“人工 智能”这个信息（后验概率）。

①如果“可能性函数”$P(B|A)/P(B)>1$，意味着“先验概率”被增强，事件A的发生的可能性变大；
②如果“可能性函数”$P(B|A)/P(B)=1$，意味着B事件无助于判断事件A的可能性；
③如果“可能性函数”$P(B|A)/P(B)<1$，意味着"先验概率"被削弱，事件A的可能性变小。

3）后验概率

$P(A|B)$称为“后验概率”，即在B事件发生之后，我们对A事件概率的重新评估。这个例子里就是在女神冲你笑后，对女神喜欢你的概率重新预测。

现在我们再回头看一遍贝叶斯公式，你现在就能明白这个公式背后的最关键思想了：
我们先根据以往的经验预估一个“先验概率”$P(A)$，然后加入新的信息（实验结果B），这样有了新的信息后，我们对事件A的预测就更加准确。

因此，贝叶斯定理可以理解成下面的式子：
后验概率（新信息出现后的A概率）＝先验概率（A概率）ｘ可能性函数（新信息带来的调整）。

贝叶斯的底层思想就是：

如果我能掌握一个事情的全部信息，我当然能计算出一个客观概率（古典概率）。

可是生活中绝大多数决策面临的信息都是不全的，我们手中只有有限的信息。既然无法得到全面的信息，我们就在信息有限的情况下，尽可能做出一个好的预测。也就是，在主观判断的基础上，你可以先估计一个值（先验概率），然后根据观察的新信息不断修正（可能性函数）。

其实阿尔法狗也是这么战胜人类的，简单来说，阿尔法狗会在下每一步棋的时候，都可以计算自己赢棋的最大概率，就是说在每走一步之后，他都可以完全客观冷静的更新自己的信念值，完全不受其他环境影响。

5.3 贝叶斯定理的应用案例

每一个医学检测，都存在假阳性率和假阴性率。所谓假阳性，就是没病，但是检测结果显示有病。假阴性正好相反，有病但是检测结果正常。

假设检测准确率是99%，如果医生完全依赖检测结果，也会误诊，即假阳性的情况，也就是说根据检测结果显示有病，但是你实际并没有得病。

举个更具体的例子，因为艾滋病潜伏期很长，所以即便感染了也可能在相当长的一段时间身体没有任何感觉，所以艾滋病检测的假阳性会导致被测人非常大的心理压力。

你可能会觉得，检测准确率都99%了，误测几乎可以忽略不计了吧？所以你觉得这人肯定没有患艾滋病了对不对？

但我们用贝叶斯分析算一下，你会发现你的直觉是错误的。

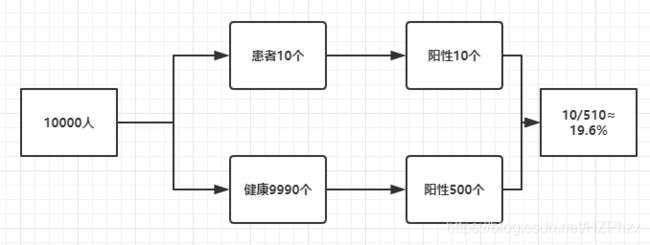
• 例子：设某种疾病的发病率是0.001，即1000人中会有1个人得病。现有一种试剂可以检验患者是否得病，它的准确率是0.99，即在患者确实得病的情况下， 它有99%的可能呈现阳性。它的误报率是5%，即在患者没有得病的情况下，它有5%的可能呈现阳性。现有一个病人的检验结果为阳性，请问他确实得病的可能性有多大？

step1分解问题：

1）要求解的问题：病人的检验结果为阳性，他确实得病的概率有多大？

病人的检验结果为阳性（新的信息）为事件B，他得病记为事件A，那么求解的就是$P(A|B)$，即病人的检验结果为阳性，他确实得病的概率。

2）已知信息：疾病的发病率是0.001，即$P(A)=0.001$。

试剂可以检验患者是否得病，准确率是0.99，即在患者确实得病的情况下（A），它有99%的可能呈现阳性（B），也就是$P(B|A)=0.99$，试剂的误报率是5%，即在患者没有得病的情况下，它有5%的可能呈现阳性得病我们记为事件A，那么没有得病就是事件A的反面，记为A’，所以这句话就是$P(B|A^{\prime })=5\%$。

step2应用贝叶斯定理：

1）求先验概率$P(A)$：

疾病的发病率是0.001，即$P(A)=0.001$。

2）求可能性函数$P(B|A)/P(B)$：

其中，$P(B|A)$表示在患者确实得病的情况下（A），试剂呈现阳性的概率，从前面的已知条件中我们已经知道$P(B|A)=0.99$。

现在只有求出$P(B)$就可以得到答案。根据全概率公式，可以求得$P(B)=P(B|A)P(A)+P(B|A^{\prime })P(A^{\prime })=0.05$。

所以可能性函数$P(B|A)/P(B)=0.99/0.05=19.8$。

3）带入贝叶斯公式求后验概率$P(A|B)$：

我们得到了一个惊人的结果，$P(A|B)=1.98\%$。

也就是说，虽然筛查的准确率都高达99%了，但是如果通过体检结果呈现阳性，真正得病概率也只有1.98%。

为什么会这样呢？我们拿艾滋病来说，由于艾滋病实在是小概率事件，所以当我们对一大群人做艾滋病筛查时，虽说准确率有99%，但仍然会有相当一部分人因为误测而被诊断为艾滋病，这一部分人在人群中的数目甚至比真正艾滋病患者的数目还要高。

造成这么不靠谱的误诊的原因，是我们无差别地给一大群人做筛查，而不论测量准确率有多高，因为正常人的数目远大于实际的患者，所以误测造成的干扰就非常大了。

根据贝叶斯定理，我们知道提高先验概率，可以有效的提高后验概率。

所以解决的办法倒也很简单，就是先锁定可疑的样本，比如10000人中检查出现问题的那10个人，再独立重复检测一次，因为正常人连续两次体检都出现误测的概率极低，这时筛选出真正患者的准确率就很高了，这也是为什么许多疾病的检测，往往还要送交独立机构多次检查的原因。

这也是为什么艾滋病检测第一次呈阳性的人，还需要做第二次检测，第二次依然是阳性的还需要送交国家实验室做第三次检测。

在《医学的真相》这本书里举了个例子，假设检测艾滋病毒，对于每一个呈阳性的检测结果，只有50%的概率能证明这位患者确实感染了病毒。但是如果医生具备先验知识，先筛选出一些高风险的病人，然后再让这些病人进行艾滋病检查，检查的准确率就能提升到95%。

6、朴素贝叶斯

了解了贝叶斯定理之后，我们来聊聊朴素贝叶斯。贝叶斯和朴素贝叶斯的概念是不同的，区别就在于“朴素”二字，朴素贝叶斯对条件个概率分布做了条件独立性的假设。

基于贝叶斯公式来估计后验概率$P(c|x)$主要困难在于类条件概率$P(x|c)$是所有属性上的联合概率，难以从有限的训练样本直接估计而得。

基于有限训练样本直接计算联合概率，在计算上将会遭遇组合爆炸问题；在数据上将会遭遇样本稀疏问题；属性越多，问题越严重。

为了避开这个障碍，朴素贝叶斯分类器采用了“属性条件独立性假设”：对已知类别，假设所有属性相互独立。换言之，假设每个属性独立的对分类结果发生影响相互独立。

基于条件独立性假设，对于$d$个属性的后验概率可以写成：
$$P(c|x)=\frac{P(c)P(x|c)}{P(x)}=\frac{P(c)}{P(x)}\prod _{i=1}^{d}P(x_i|c)$$
$d$为属性数目，$x_i$是$x$在第$i$个属性上取值。

贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。而朴素朴素贝叶斯分类是贝叶斯分类中最简单，也是常见的一种分类。

从数学角度来说，分类问题可做如下定义：已知集合$C=\{y_1,y_2,...y_n\}$，$I=\{x_1,x_2,...x_n\}$，确定映射规则$y=f(x)$，使得任意$x_i\in I$，有且仅有一个$y_i\in C$，使得$y_i=f(x_i)$成立。

其中$C$叫做类别集合，其中每一个元素是一个类别，而$I$叫做项集合（特征集合），其中每一个元素是一个待分类项，$f$叫做分类器。分类算法的任务就是构造分类器$f$。

分类算法的内容是要求给定特征，让我们得出类别，这也是所有分类问题的关键。

回顾贝叶斯公式：
$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$
换个表达形式就会明朗很多，如下：
$$P(类别|特征)=\frac{P(特征|类别)P(类别)}{P(特征)}$$

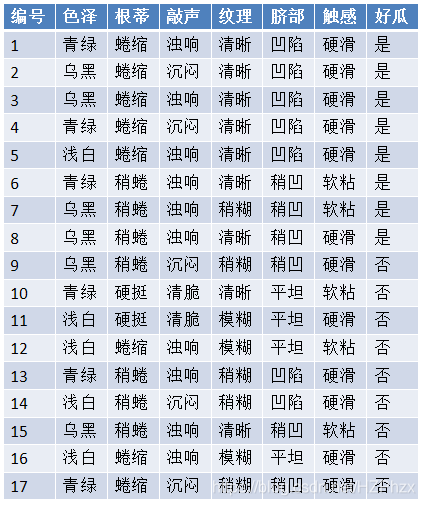
【例子】给定数据如下：

现在给我们的问题是，如果一男生想向女生求婚，男生的四个特点分别是不帅，性格不好，身高矮，不上进，请你判断一下女生是嫁还是不嫁？

这是一个典型的分类问题，转为数学问题就是比较$p(嫁|不帅、性格不好、身高矮、不上进)$与$p(不嫁|不帅、性格不好、身高矮、不上进)$的概率，谁的概率大，我就能给出嫁或者不嫁的答案！

这里我们联系到朴素贝叶斯公式：
$$p(嫁|不帅、性格不好、身高矮、不上进)=\frac{p(不帅、性格不好、身高矮、不上进|嫁)\ast p(嫁)}{p(不帅、性格不好、身高矮、不上进)}$$

那么我只要求得$p(不帅、性格不好、身高矮、不上进|嫁)、p(不帅、性格不好、身高矮、不上进)、p(嫁)$，就能得到最终结果。

前面我们提到朴素贝叶斯分类“朴素”一词的来源，朴素贝叶斯算法是假设各个特征之间相互独立，那么下面等式就成立了！

$$p(不帅、性格不好、身高矮、不上进|嫁)=p(不帅|嫁)\ast p(性格不好|嫁)\ast p(身高矮|嫁)\ast p(不上进|嫁)$$

$$p(不帅、性格不好、身高矮、不上进)=p(不帅)\ast p(性格不好)\ast p(身高矮)\ast p(不上进)$$

【为什么需要假设特征之间相互独立呢】
1、我们这么想，假如没有这个假设，那么我们对右边这些概率的估计其实是不可做的，这么说，我们这个例子有4个特征，其中帅包括{帅，不帅}，性格包括{不好，好，爆好}，身高包括{高，矮，中}，上进包括{不上进，上进}，那么四个特征的联合概率分布总共是4维空间，总个数为2×3×3×2=36个。

36个，计算机扫描统计还可以，但是现实生活中，往往有非常多的特征，每一个特征的取值也是非常之多，那么通过统计来估计后面概率的值，变得几乎不可做，这也是为什么需要假设特征之间独立的原因。

2、假如我们没有假设特征之间相互独立，那么我们统计的时候，就需要在整个特征空间中去找，比如统计$p(不帅、性格不好、身高矮、不上进|嫁)$。

我们就需要在嫁的条件下，去找四种特征全满足分别是不帅，性格不好，身高矮，不上进的人的个数，这样的话，由于数据的稀疏性，很容易统计到0的情况。 这样是不合适的。

根据上面两个原因，朴素贝叶斯法对条件概率分布做了条件独立性的假设，由于这是一个较强的假设，朴素贝叶斯也由此得名！这一假设使得朴素贝叶斯法变得简单，但有时会牺牲一定的分类准确率。

因此，我们将上面公式整理一下如下：
$$p(嫁|不帅、性格不好、身高矮、不上进)=\frac{p(不帅、性格不好、身高矮、不上进|嫁)\ast p(嫁)}{p(不帅、性格不好、身高矮、不上进)}=\frac{p(不帅|嫁)\ast p(性格不好|嫁)\ast p(身高矮|嫁)\ast p(不上进|嫁)\ast p(嫁)}{p(不帅)\ast p(性格不好)\ast p(身高矮)\ast p(不上进)}$$

下面我们一个一个的统计计算：
$$p(嫁)=\frac{6}{12}=\frac{1}{2}$$
$$p(不帅|嫁)=\frac{3}{6}=\frac{1}{2}，p(性格不好|嫁)=\frac{1}{6}，p(矮|嫁)=\frac{1}{6}，p(不上进|嫁)=\frac{1}{6}$$
$$p(不帅)=\frac{4}{12}=\frac{1}{3}，p(性格不好)=\frac{4}{12}=\frac{1}{3}，p(矮)=\frac{7}{12}，p(不上进)=\frac{4}{12}=\frac{1}{3}$$

则$$p(嫁|不帅、性格不好、身高矮、不上进)=\frac{\frac{1}{2}\times \frac{1}{6}\times \frac{1}{6}\times \frac{1}{6}\times \frac{1}{2}}{\frac{1}{3}\times \frac{1}{3}\times \frac{7}{12}\times \frac{1}{3}}$$

同理，我们可以计算$$p(不嫁|不帅、性格不好、身高矮、不上进)=\frac{\frac{1}{6}\times \frac{1}{2}\times 1\times \frac{1}{2}\times \frac{1}{2}}{\frac{1}{3}\times \frac{1}{3}\times \frac{7}{12}\times \frac{1}{3}}$$

很显然，$$p(不嫁|不帅、性格不好、身高矮、不上进)>p(嫁|不帅、性格不好、身高矮、不上进)$$

所以我们根据朴素贝叶斯算法可以给这个女生答案，是不嫁！！！！

【朴素贝叶斯分类的优缺点】

优点：

1. 朴素贝叶斯模型有稳定的分类效率。
2. 对小规模的数据表现很好，能处理多分类任务，适合增量式训练，尤其是数据量超出内存时，可以一批批的去增量训练。
3. 对缺失数据不太敏感，算法也比较简单，常用于文本分类。

缺点：

1. 理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型给定输出类别的情况下,假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。
2. 需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。
3. 由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。
4. 对输入数据的表达形式很敏感。

7、拉普拉斯平滑修正

零概率问题，就是在计算实例的概率时，如果某个量$x$，在观察样本库（训练集）中没有出现过，会导致整个实例的概率结果是0。

在实际的模型训练过程中，可能会出现零概率问题（因为先验概率和反条件概率是根据训练样本算的，但训练样本数量不是无限的，所以可能出现有的情况在实际中存在，但在训练样本中没有，导致为0的概率值，影响后面后验概率的计算）。

即便可以继续增加训练数据量，但对于有些问题来说，数据怎么增多也是不够的。这时我们说模型是不平滑的，我们要使之平滑，一种方法就是将训练（学习）的方法换成贝叶斯估计。

【朴素贝叶斯算法的先天缺陷】

其他属性携带的信息被训练集中某个分类下未出现的属性值“抹去”，造成预测出来的概率绝对为0。为了弥补这一缺陷，前辈们引入了拉普拉斯平滑的方法：对先验概率的分子(划分的计数)加1，分母加上类别数；对条件概率分子加1，分母加上对应特征的可能取值数量。这样在解决零概率问题的同时，也保证了概率和依然为1：

$$P(c)=\frac{|D_c|}{|D|}\to P(c)=\frac{|D_c|+1}{|D|+N}$$
$$P(x_i|c)=\frac{|D_{x_i|c|}}{|D_c|}\to P(x_i|c)=\frac{|D_{x_i|c|}+1}{|D_c|+N_i}$$

其中，$N$表示数据集中分类标签，$N_i$表示第$i$个属性的取值类别数，$|D|$样本容量，$|D_c|$表示$c$类别的记录数量，$|D_{x_i|c}|$表示类别$c$中第$i$个属性取值为$x_i$的记录数量。

将这两个式子应用到上面的计算过程中，就可以弥补朴素贝叶斯算法的这一缺陷问题。

• 例子：西瓜的数据：
  

【未使用拉普拉斯平滑之前】

当我们计算P(好瓜=是)时，样本有17个，所以$|D|=17$，好瓜标签可以分为｛是，否｝两类，所以$N=2$，(好瓜=是)的样本个数有8个，所以这里$|D_c|=8$。

$$P(好瓜=是)=\frac{|D_c|}{|D|}=\frac{8}{17}$$

计算P(敲声=清脆|好瓜=是)时，(好瓜=是)的样本有8个，所以$|D_c|=8$，敲声标签可以分为｛浊响，沉闷，清脆｝三类，所以$N=3$，(敲声=清脆|好瓜=是)的样本个数有0个，所以这里$|D_{x_i,c}|=0$。

$$P(敲声=清脆|好瓜=是)=\frac{|D_{x_i,c|}}{|D_c|}=\frac{0}{8}$$

不论样本的其他属性如何，分类结果都会为“好瓜=否”，这样显然不太合理。

【使用拉普拉斯平滑之后】

当我们计算P(好瓜=是)时，样本有17个，所以$|D|=17$，好瓜标签可以分为｛是，否｝两类，所以$N=2$，(好瓜=是)的样本个数有8个，所以这里$|D_c|=8$。

$$P(好瓜=是)=\frac{|D_c|+1}{|D|+N}=\frac{8+1}{17+2}$$

计算P(敲声=清脆|好瓜=是)时，(好瓜=是)的样本有8个，所以$|D_c|=8$，敲声标签可以分为｛浊响，沉闷，清脆｝三类，所以$N_i=3$，(敲声=清脆|好瓜=是)的样本个数有0个，所以这里$|D_{x_i,c}|=0$。

$$P(敲声=清脆|好瓜=是)=\frac{|D_{x_i,c|}+1}{|D_c|+N_i}=\frac{0+1}{8+3}$$

显然结果不是0，使结果变得合理。

8、半朴素贝叶斯

9、EM算法