上采样（upsample）和 反卷积（deconvolution）

相关论文推荐：A guide to convolution arithmetic for deep learning

1 卷积

可以看一下这篇文章：https://blog.csdn.net/weixin_42468475/article/details/108628474

2 上采样

在应用在计算机视觉的深度学习领域，由于输入图像通过卷积神经网络(CNN)提取特征后，得到的特征图（Feature maps）尺寸往往会变小，而有时我们需要将图像恢复到原来的尺寸以便进行进一步的计算(e.g.:图像的语义分割、定位)，这个采用扩大图像尺寸，实现图像由小分辨率到大分辨率的映射的操作，叫做上采样(Upsample)。

上采样有3种常见的方法：双线性插值(bilinear)，反卷积(Transposed Convolution)，反池化(Unpooling)，我们这里只讨论反卷积。

CAM 和 Grad-CAM 都用到了基于双线性插值的上采样技术。参见：https://blog.csdn.net/weixin_42468475/article/details/121761144

3 反卷积

参考文献：M. D. Zeiler and R. Fergus. Visualizing and understanding convolutional networks. In ECCV, 2014. 2, 3, 4, 6, 8, 10, 14

反卷积，也叫转置卷积，它并不是正向卷积的完全逆过程，用一句话来解释：

反卷积是一种特殊的正向卷积，先按照一定的比例通过补 0 来扩大输入图像的尺寸，接着旋转卷积核，再进行正向卷积。

• 反卷积的本质还是卷积

• 反卷积可以用于扩大图像 （常用于上采样）

3.1 反卷积的数学推导

正向卷积的实现过程

假设输入图像 input 尺寸为 $4\times 4$ ，元素矩阵为：

卷积核 kernel 的尺寸为 $3\times 3$，元素矩阵为：

我们设定步长stride=1，填充padding=0，即 $i=4,k=3,s=1,p=0$，按照卷积公式计算，根据：
输出图像的尺寸应为 $2\times 2$ 。

用矩阵乘法描述卷积

把 input 的元素矩阵展开成一个列向量 X：

把输出图像 output 的元素矩阵展开成一个列向量 Y：

对于输入的元素矩阵 X 和 输出的元素矩阵 Y，用矩阵运算描述这个过程：

通过推导，我们可以得到稀疏矩阵 $C$ ：

反卷积的操作就是要对这个矩阵运算过程进行逆运算，即通过 $C$ 和 X 得到 Y ，根据各个矩阵的尺寸大小，我们能很轻易的得到计算的过程，即为反卷积的操作：

但是，如果你代入数字计算会发现，反卷积的操作只是恢复了矩阵 X 的尺寸大小，并不能恢复 X 的每个元素值，只能保证矩阵大小一致。

在此之前，我们先给出反卷积图像尺寸变化的公式。

反卷积的输入输出尺寸关系

在进行反卷积时，简单来说，大体上可分为以下两种情况：

卷积和反卷积的关系

卷积 (论文中的 Relationship 6)：

反卷积 (论文中的 Relationship 14)

上面两个式子中, 不带一撇的是卷积操作的参数, 带一撇的是反卷积操作的参数, 进一步地, 他们存在如下的关系：

实际上卷积和反卷积只是两个有关联的操作，但他们并不是互为逆运算的，仅仅是在形状上存在互逆的关系(所以上面的式子也都是跟形状有关的参数)。实际上形状上互逆也就够了，毕竟我们通常使用反卷积只是为了成倍地扩大特征图。

Relationship 1：

此时反卷积的输入输出尺寸关系为：

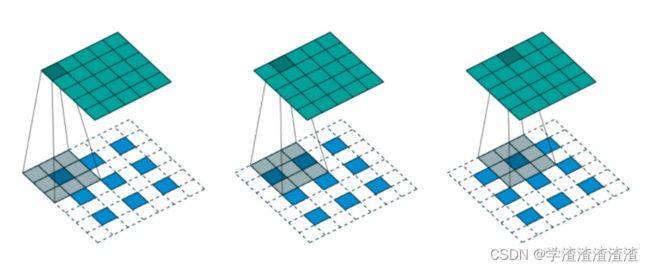
如上图所示，我们选择一个输入 input 尺寸为 $3\times 3$ ，卷积核尺寸为 $4\times 4$ ，步长=2，填充=1 ，即 $i=3,k=3,s=2,p=1$ ，则输出 output 的尺寸为 $o=2\times (3-1)+4-2\times 1=5$，即 $6\times 6$ 的大小。

3.3 反卷积的应用

在例如Resnet、Googlenet的网络中，经最后一层卷积层输出的若干特征图尺寸是 $7\times 7$ ，如下图，最后一层卷积层输出的就是 512个$7\times 7$ 的特征图：

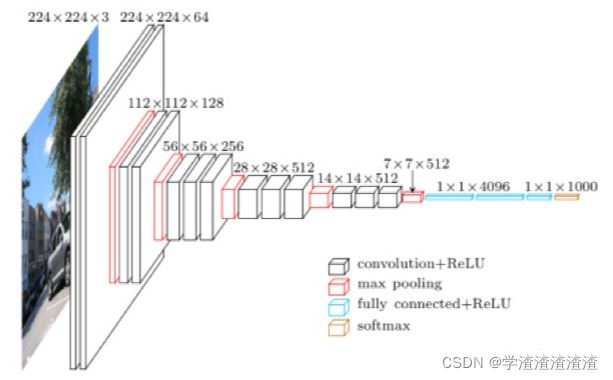
若我们要对其进行上采样，上采样反卷积操作的输入每张图像的尺寸是 $7\times 7$ ，我们希望进行一次上采样后能恢复成原始图像的尺寸 $224\times 224$ ，代入公式：

根据上式，我们可以得到一个关于 $s,k,p$ 三者之间关系的等式：

通过实验，最终找出了最合适的一组数据：
$s=32,p=16,k=64$

3.4 利用pytorch验证反卷积的计算

同 3.3 节的设置，验证代码如下：

import torch
from torch import nn

# 定义小图像
small_mat = torch.randn([1,1,7,7])

# 先进行反卷积，得到大图像
deconv = nn.ConvTranspose2d(in_channels=1, out_channels=1, kernel_size=64, stride=32)
big_mat = deconv(small_mat)

# 再进行反卷积，得到小图像
conv = nn.Conv2d(in_channels=1, out_channels=1, kernel_size=64, stride=32)
small_mat2 = conv(big_mat)

我们来看看shape对不对：


shape是对的，虽然复原后的 small_mat2 和 small_mat 形状一样，但是数值是不一样的：

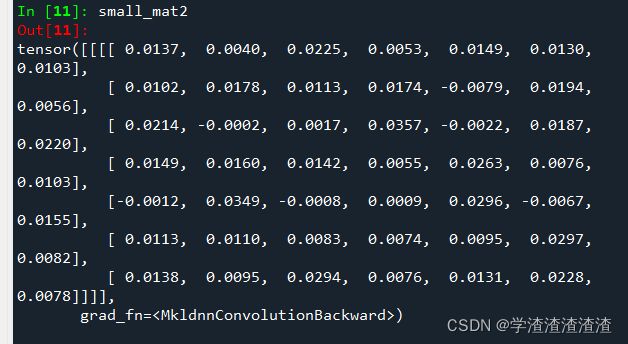
为了形象生动的展现。

参考

https://www.zhihu.com/question/48279880