XGBoost, LightGBM

Adaboost, GBDT

XGBoost (eXtreme Gradient Boosting)

极致 GBDT

Ref

• paper: XGBoost: A Scalable Tree Boosting System
• XGBoost 的原理、公式推导、Python 实现和应用

---

• XGBoost 是一个优化的分布式梯度提升库，它的基本思想和 GBDT 相同，但是做了一些优化，比如二阶导数使损失函数更精准；正则项避免树过拟合；Block 存储可以并行计算等

Regularized Learning Objective

• 训练数据集为 $\mathcal{D}=\{(x_i,y_i)\}$ ($|\mathcal{D}|=n,x_i\in {\mathbb{R}}^m,y_i\in \mathbb{R}$)，提升树模型 $\varphi$ 为一个加法模型：
  其中 $f$ 为 CART 回归树
• 定义如下的目标函数：
  其中 $l$ 为经验损失 (a differentiable convex loss function)，$\Omega$ 为结构损失，$T$ 为 CART 回归树的叶结点数，$w$ 为 CART 回归树叶结点对应的权重 (模型的输出即为输入样本对应叶结点的权重)
  

---

正则项中的 $\frac{1}{2}\lambda ||w|{|}^2$ 如何理解？

• Ref: XGBoost 中的正则项为什么包含树模型的输出值？
• 这里需要把加法模型和过拟合结合起来，因为最后输出是加上当前树的输出值，如果这棵树的输出值接近 0，那么最后的输出值受这棵树的影响就很小，不容易过拟合
• 还可以从另一角度解释 (这部分内容可以先看后续小节内容再回来理解)：XGBoost 在建树时，如果采用预剪枝策略，那么当 ${\mathcal{L}}_{split}<0$ 时就会停止结点分裂。如果 $\lambda$ 很大，在 $\gamma$ 不变的情况下，结点就更容易被剪枝，从而生成更简单的回归树，进一步避免了过拟合
  $${\mathcal{L}}_{split}=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{(G_L+G_R{)}^2}{(H_L+H_R)+\lambda }]-\gamma$$

下面的目标就是求解出最优的 $k$ 个 CART 回归树使得上述目标函数最小

Gradient Tree Boosting (How do we Learn)

• boosting 在训练时采用前向分步算法，每次只训练一个基学习器，因此我们下面就考虑在已经学得前 $t-1$ 个基学习器的情况下，需要怎样学得第 $t$ 个基学习器使得目标函数值下降

---

• 在训练第 $t$ 个基学习器时，目标函数可写为如下形式 (前 $t-1$ 个基学习器的正则项与当前的优化目标无关，因此可以直接消去)：
  
• 将 $l(y_i,x)$ 在 ${\hat{y}}_i^{(t-1)}$ 处进行二阶泰勒展开，可得
  其中 $g_i=\frac{\partial l(y_i,{\hat{y}}_i)}{\partial {\hat{y}}_i}{\mid }_{\hat{y}={\hat{y}}^{(t-1)}},h_i=\frac{{\partial }^{2}l(y_i,{\hat{y}}_i)}{\partial {\hat{y}}_i^2}{\mid }_{\hat{y}={\hat{y}}^{(t-1)}}$。在进一步消除常数项后就得到了如下的目标函数：
  

注意，在 GBDT 中，${\tilde{\mathcal{L}}}^{(t)}={\sum }_{i=1}^{n}l(y_i,{\hat{y}}_i^{(t-1)}+f_t(x_i))\approx {\sum }_{i=1}^n[l(y_i,{\hat{y}}_i^{(t-1)})+g_i{f}_t(x_i)]$，然后取 $f_t(x_i)=-g_i$ 即可使目标函数值下降；通过对比可以看出，XGBoost 相对于 GBDT，使用二阶泰勒展开更加精准，同时还增加了正则项避免模型过拟合

• 将所有训练样本按叶结点进行分组，可得
  其中 $I_j$ 表示属于叶结点 $j$ 的训练样本集合
• 设 $G_j$ 为叶结点 $j$ 所含样本的一阶偏导数的累加和，是一个常数；$H_j$ 为叶结点 $j$ 所含样本的二阶偏导数的累加和，也是一个常数：
  $$G_j=\sum _{i\in I_j}{g}_j,H_j=\sum _{i\in I_j}{h}_j$$则目标函数变为
  $${\tilde{\mathcal{L}}}^{(t)}=\sum _{j=1}^T[G_j{w}_j+\frac{1}{2}(H_j+\lambda )w_j^2]+\gamma T$$

---

• 现在假设 CART 回归树的结构已经确定，则上面的目标函数只与叶结点的权值 $w$ 有关。因此可以计算出 $w_j^{\ast }$：
  $$w_j^{\ast }=\underset{w_j}{\mathrm{argmin}}[G_j{w}_j+\frac{1}{2}(H_j+\lambda )w_j^2]=-\frac{G_j}{H_j+\lambda }$$此时的目标函数值为
  $${\tilde{\mathcal{L}}}^{(t)}(q)=-\frac{1}{2}\sum _{j=1}^T\frac{G_j^2}{H_j+\lambda }+\gamma T$$其中 $q$ 表示 CART 回归树的结构，用于将样本点映射到回归树的叶结点上
• ${\tilde{\mathcal{L}}}^{(t)}(q)$ 可以被当作结构得分用来衡量树结构的好坏，得分越低，树的结构越好；因此现在我们的任务就是找到得分最低的结构，然后根据 $w_j^{\ast }=-\frac{G_j}{H_j+\lambda }$ 计算出叶结点的权重即可得到我们想要的第 $t$ 个基学习器
  
• 当然直接枚举出所有树结构 $q$，对每个 $q$ 计算结构得分是不现实的。因此我们可以采用基于结构得分的启发式规则进行建树 (类似于基于信息增益、基尼指数的启发式规则)
  • 假设当前有一个树结点，我们尝试对它进行分裂。设 $I_L$ 和 $I_R$ 分别为分裂后左右子结点对应的样本集，$I=I_L\cup I_R$，那么在分裂后目标值的减小量为
    $${\mathcal{L}}_{split}=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{(G_L+G_R{)}^2}{(H_L+H_R)+\lambda }]-\gamma$$我们在建树时，每个结点都寻找 ${\mathcal{L}}_{split}$ 最大的那个分裂点进行分裂即可 (${\mathcal{L}}_{split}$ 就类似于信息增益，可以看作分裂后的收益)
  • 那么如何找到最佳分裂点呢？(需要找到需要分裂的结点，属性，以及阈值) (find the best split)

Split Finding Algorithms

Basic Exact Greedy Algorithm

贪心算法枚举所有可能的分裂，从中选取 ${\mathcal{L}}_{split}$ 最大的那个

• 对每个结点，遍历全部 $d$ 个属性
  • 对每个属性，先将结点中的样本按属性值排序 (先排序，方便在线性扫描时累加 $g_i$ 和 $h_i$)，然后使用线性扫描来决定该属性的最佳分裂阈值，得到该属性的最佳分裂方案
  • 选取所有属性中的最佳分裂方案对该结点进行分裂

---

剪枝

• 预剪枝：当 ${\mathcal{L}}_{split}<0$ 时停止分裂，但此时 ${\mathcal{L}}_{split}<0$ 的分支在后续继续分裂后可能会带来比较好的效果
• 后剪枝：让树生长到最大深度，然后自底向上对 ${\mathcal{L}}_{split}<0$ 的结点进行剪枝

---

时间复杂度

• 对于一棵 $K$ 层回归树，每层都要枚举所有 $d$ 个属性并对全部 $n$ 个样本按照该属性值进行排序，然后再通过线性扫描找出该层每个结点的最佳分裂，因此时间复杂度为
  $$T(n)=O(K\times d\times (n\log n+n))=O(Kdn\log n)$$

如果保存所有样本相对于 $d$ 个属性的排序顺序，那么就可以将时间复杂度进一步优化为 $T(n)=O(dn\log n+Kdn)$

Approximate Algorithm

Ref

• Need help understanding xgboost’s approximate split points proposal
• Wiki: Quantile
• Xgboost 近似分位数算法

---

• 当数据多到无法一次性放入内存或采用分布式训练时，Basic Exact Greedy Algorithm 就没那么高效了，此时可以采取一种近似算法
• 对于每个特征，近似算法先根据特征分布的分位数 (percentile) 找到一系列的候选分裂点 (candidate split points)，然后在候选分裂点中选出最佳分裂点进行划分

---

分位数 (Quantile)

• In statistics and probability, quantiles are cut points dividing the range of a probability distribution into continuous intervals with equal probabilities, or dividing the observations in a sample in the same way.
• $q$-quantiles are values that partition a finite set of values into $q$ subsets of (nearly) equal sizes
  • e.g. 如果有 20 个排序好的样本点 $\{x_1,..,x_{20}\}$，那么 10-quantiles 对应的样本点就是 $\{x_2,x_4,..,x_{18}\}$ (均匀地将样本集划分为 10 个子集)，它们的值分别至少比样本集中的 $\{10\%,20\%,...,90\%\}$ 的样本更大
  • e.g. 对于正态分布，4-quantiles 对应样本点 $\{Q_1,Q_2,Q_3\}$
    

---

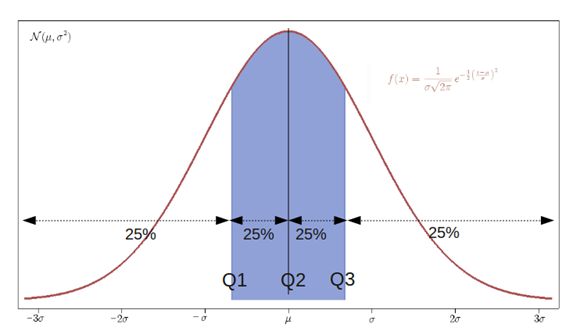
加权分位数 (Weighted Quantile)

• 在训练第 $t$ 个基学习器时，所有样本的重要性是不同的，也就是说，不同样本拥有不同权重，例如有的样本比较难预测，那么它的权重就比较大，有的样本已经被前 $t-1$ 个基学习器轻松预测，那么它的权重就比较小
• 因此，我们不再使用分位数，而是使用加权分位数，此时 10-quantiles 对应的第一个划分点就不再意味着比它值小的样本点有 10%，而是比它值小的样本点所占的权重为 10%。有了加权分位数，我们就能更多地选择那些权重更大、更重要的样本点作为候选分裂点
• 那么如何定义每个样本的权重呢？我们可以对目标函数作如下变换：
  $$\begin{array}{rl}{\tilde{L}}^{(t)}& =\sum _{i=1}^n[g_i{f}_t(x_i)+\frac{1}{2}{h}_i{f}_t^2(x_i)]+\Omega (f_t)\\ & =\sum _{i=1}^n\frac{1}{2}{h}_i[f_t(x_i{)}^2+2\frac{g_i{f}_t(x_i)}{h_i}+(\frac{g_i}{h_i}{)}^2]+\Omega (f_t)-\sum _{i=1}^n(\frac{g_i}{h_i}{)}^2\\ & =\sum _{i=1}^n\frac{1}{2}{h}_i[(f_t(x_i)+\frac{g_i}{h_i}{)}^2]+\Omega (f_t)+constant\\ & =\frac{1}{2}\sum _{i=1}^n{h}_i[(f_t(x_i)-(-\frac{g_i}{h_i}){)}^2]+\Omega (f_t)+constant\end{array}$$可以看出，上式为一个加权平方损失的形式，每个样本的标签值为 $-\frac{g_i}{h_i}$，权重为 $h_i$
  • e.g. 若损失函数为平方误差 $l({\hat{y}}_i,y_i)=\frac{1}{2}({\hat{y}}_i-y_i{)}^2$，那么 $h_i=1$，每个样本的权重是相同的；若模型输出 $y_i$ 接 Sigmoid 函数得到 $z_i$，损失函数为对数损失，则 $l({\hat{y}}_i,y_i)=-y_i\log z_i-(1-y_i)\log (1-z_i)$，则 $g_i=z_i-y_i,h_i=z_i(1-z_i)$，因此当样本预测概率在 0.5 时权重最大 (0.5 表示模型无法确定该样本到底是正例还是负例)
    

---

候选分裂点 (加权分位数)

• 设第 $k$ 个属性对应样本集为 ${\mathcal{D}}_k=\{(x_{1k},h_1),...,(x_{nk},h_n)\}$。定义函数 $r_k(z)$ 表示在第 $k$ 个属性上比样本 $z$ 的值更小的样本点对应的权重和所占百分比：
  
• 按照加权分位数的思想，第 $k$ 个属性对应的候选分裂点 $\{s_{k1},...s_{kl}\}$ 满足
  (也就相当于 $1/ϵ$-quantiles)

使用 Quantile 选取候选分裂点有利于分布式训练

由于数据量很大或正在进行分布式学习，我们还需要一个快速找到加权分位点 (i.e. 候选分割点) 的算法，这将在 Weighted Quantile Sketch 一节中介绍

---

根据候选分裂点找出最佳分裂点

• 根据候选分裂点找出最佳分裂点，需要统计每个候选分裂点对应的梯度数据 $G_L,G_R$ 和 $H_L,H_R$。因此可以将样本点按照候选分割点对应的权重百分比进行分桶 (bucket)，例如当 $ϵ=0.1$ 时，权重占比为 $0\sim 10\%,10\%\sim 20\%...$ 的样本各分到不同桶中，然后计算 $G$ 和 $H$
• 在得到每个候选分裂点对应的 $G$ 和 $H$ 后，就可以用 Basic Exact Greedy Algorithm 中的方法，根据候选分裂点找出最佳分裂点

• 上述算法还有两个变种：全局算法和局部算法，它们的区别就是选择候选分裂点的时机不同
  • 全局算法在开始建树之前就选出所有的候选分裂点，并在树的所有层的构建中都使用这些候选分裂点
  • 局部算法在每次分裂后都为结点重新选出新的候选分裂点
  • 可以直观地感受到，局部算法由于在每次分裂后都重新提出候选分裂点，因此适合构造更深的树；而全局算法如果想要达到与局部算法相同的性能，就需要一次提出更多的候选分裂点 (即更小的 $ϵ$)
    

XGBoost 系统只在单机模式下支持 Basic Exact Greedy Algorithm，在单机和分布式模式下都支持 local/global Approximate Algorithm

Weighted Quantile Sketch (加权分位数草图法)

• 之前提到，我们还需要一个快速找到加权分位点 (i.e. 候选分割点) 的算法。对此，XGBoost 采用了一种分布式的加权分位数草图算法 (distributed weighted quantile sketch algorithm) 来找到候选分割点

---

• The general idea is to propose a data structure that supports merge and prune operations, with each operation proven to maintain a certain accuracy level.
• 这个算法看起来还有些复杂，具体可以参考论文的附录 A

Sparsity-aware Split Finding (稀疏感知法)

• Ref: 还有人不懂 XGBoost 的缺失值处理？(全面解析篇)

---

Sparse Dataset

• 如果数据本身含有很多 0 值或缺失值，又或者是使用 one-hot encoding 等技术，数据集就会变得很稀疏

---

训练阶段

• 在训练过程中，如果特征 $k$ 出现了缺失值，处理步骤如下：
  • (1) 对于特征 $k$ 非缺失的数据，计算出 ${\mathcal{L}}_{split}$ 并比较大小，选出最大的 ${\mathcal{L}}_{split}$，确定其为分裂节点
  • (2) 对于特征 $k$ 缺失的数据，将缺失值分别划分到左子树和右子树并计算 ${\mathcal{L}}_{split}$，选出更大的 ${\mathcal{L}}_{split}$，将该方向作为缺失值的分裂方向 (记录下来，预测阶段将会使用)

$${\mathcal{L}}_{split}=\frac{1}{2}[\frac{G_L^2}{H_L+\lambda }+\frac{G_R^2}{H_R+\lambda }-\frac{(G_L+G_R{)}^2}{(H_L+H_R)+\lambda }]-\gamma$$

---

预测阶段

• 在预测阶段，如果特征 $k$ 出现了缺失值，则可以分为以下两种情况：
  • (1) 如果训练过程中，特征 $k$ 出现过缺失值，则按照训练过程中缺失值划分的方向 (left or right)，进行划分
  • (2) 如果训练过程中，特征 $k$ 没有出现过缺失值，将缺失值的划分到默认方向 (左子树)

---

---

Discussion

• XGBoost 使用一个统一的方式 (Algorithm 3) 来处理稀疏数据 (0 值、缺失值…) (因此，如果样本属性中需要包含类别属性，那么就可以直接将类别属性转化为 one-hot encoding 的形式来处理，而不必将类别属性与连续属性分开考虑)
• 同时，上述算法能使计算复杂度与非稀疏样本的数量保持线性关系，当数据集非常稀疏时，上述算法能大幅增加计算速度
  

XGBoost 可以自动处理缺失值，而 GBDT 却没有专门针对缺失值进行处理

Shrinkage and Column Subsampling

• 除了目标函数中的正则项，XGBoost 还引入了 Shrinkage 和 Column Subsampling 技术来进一步防止过拟合

---

Shrinkage

• Shrinkage 通过在前向分步算法中，给每个新增的基学习器乘上一个系数 $\eta$ 来减少单一决策树对整体模型的影响，并将剩余的优化空间留给后续要学习的基学习器进行优化
  $$y^{(t)}=y^{(t-1)}+\eta f_t(x_i)$$通常设置 $\eta =0.1$，然后迭代次数设置得大一点

---

Column (feature) Subsampling

• 在对同一层内每个节点进行分裂之前，先随机选择一部分特征，然后遍历这部分特征来寻找最优分裂方案
• Column Subsampling 不仅可以避免过拟合，还有利于并行算法的加速

System Design

• Ref: Xgboost 系统设计：分块并行、缓存优化和 Blocks for Out-of-core Computation

Column Block for Parallel Learning

• 在树的学习过程中，最耗时的部分就是对数据进行排序。XGBoost 对此进行了优化

---

Compressed Sparse Column (CSC) Format

• Ref: 理解 Compressed Sparse Column Format (CSC)
• CSC 是一种按列存储稀疏矩阵的格式。给定一个矩阵，CSC 记录矩阵的行数 $numRows$、列数 $numCols$、按列主序遍历得到的非零值 $values$、非零值对应的行数 $rowIndices$、每一列中第一个非零值对应的序号 $colPtrs$
  • e.g. 对于矩阵 $\left[\begin{array}{ccc}1& 0& 4\\ 0& 3& 5\\ 2& 0& 6\end{array}\right]$，$numRows=numCols=3$，$values=[1,2,3,4,5,6]$，$rowIndices=[0,2,1,0,1,2]$，$colPtrs=[0,2,3]$
• 可以看出，CSC 格式按列访问非零值是非常方便的

---

提前排序

• 为了减少排序时间，XGBoost 将 $n\times d$ 的数据矩阵以 CSC 格式存储在内存块 (block) 中，并在存储时，将每一列都按照对应的特征值进行排序。这样后续算法中就不用再重新进行排序了
  • 在 Exact greedy algorithm 中，可以将全部数据集都存在一个 Block 中，然后按列遍历一次排序好的数据就能找到当前层所有叶结点的最佳分裂点。这样，算法的时间复杂度由 $O(Kdn\log n)$ 降为 $O(Kdn)$
    (注意上图中，缺失值是和零值以同样的方式进行处理的)
  • 在 Approximate algorithm 中，可以将数据集存放在多个 Block 中，每个 Block 都存储数据集的某几行 (部分样本)，不同的 block 可以存放在不同机器或磁盘中。这样仅需对排序好的列进行一次线性扫描即可找到候选分裂点，这对 local 版本的近似算法尤其友好
• 并行化：可以对每个列的数据采集进行并行化处理
• Column Subsampling：这样的存储方式同样非常适合 Column Subsampling 的部署

---

时间复杂度分析

• Ref: XGBoost paper - time complexity analysis
• 设 $d$ 为树的最大深度，$K$ 为树的数量，$||x|{|}_0$ 为训练数据中非零项的数量
  • 对于 exact greedy algorithm，原始的 spase aware algorithm 的时间复杂度为 $O(Kd||x|{|}_0\log n)$ (每次排序的时间复杂度不会超过 $||x|{|}_0\log n$)；而使用 Column block 结构后，时间复杂度降至 $O(Kd||x|{|}_0+||x|{|}_0\log n)$，其中 $O(||x|{|}_0\log n)$ 为一次排序所需开销
  • 对于 approximate algorithm，原始算法的时间复杂度为 $O(Kd||x|{|}_0\log q)$ ($q$ 为候选分裂点的数目)；而使用 Column block 结构后，时间复杂度降至 $O(Kd||x|{|}_0+||x|{|}_0\log B)$ ($B$ 为每个 Block 中的最大行数，即最大样本数；这里 $O(||x|{|}_0\log B)$ 的时间复杂度应该是考虑的并行处理时的时间复杂度)

Cache-aware Access

• 虽然通过 Column Block 结构可以优化分裂点的查找，但在查找过程中，我们却需要通过数据的行索引来获取梯度数据并进行累加。然而，梯度数据是按照样本原来的顺序排列的，这就会导致不连续的内存访问，进而引起 Cache miss 带来 stall，而累加带来的短距离数据依赖也会使得后续指令无法被执行，这会显著影响程序的执行效率
  
  • 对于 exact greedy algorithm，可以通过 缓存预取 (cache-aware prefetching algorithm) 来缓解上述问题。具体来说，就是给每个线程都分配一个内部 buffer 并将梯度数据提前预取到 buffer 中，然后以 mini-batch 的形式进行累加，这可以使梯度数据的访问变得连续，并且将短距离数据依赖调整为一个更长距离的数据依赖。缓存预取在样本数很多的情况下比较有效：
    
  • 对于 approximate algorithm，可以通过选择合适的 Block size来解决。Block size 指一个 Block 最多能存放的样本数，它反映了存储梯度数据所需的 Cache 开销。Block size 过小会导致并行化程度不高，而过大则会导致更多的 Cache miss。在 paper 中，通过实验得出 $2^{16}$ 是一个比较合适的 Block size
    

Blocks for Out-of-core Computation

核外 Block 计算

• 如果数据量太大无法一次放入内存，就需要将数据分为多个 Block 保存在磁盘上。为了减少磁盘的读开销，需要使用一个独立的线程来将 Block 预读入主存，这样就可以并行化计算和读磁盘这两个过程。但读磁盘的速度实在太慢，因此还需要进一步增加磁盘 IO 吞吐量。为此，XGBoost 采用了两个技术：
  • (1) Block Compression：Block 内存储的数据按列压缩 (LZ4 compression)，然后在独立线程将 Block 数据读入内存的同时进行解压。对于行索引，可以将所有行索引都减去 Blcok 开始的索引 (substract the row index by the begining index of the block)，由此转换为相对于 Block 的偏移量。在 Cache-aware Access 中提到，合适的 Block Size 是 $2^{16}$，因此每个偏移量只需要用一个 16 位整数来记录
  • (2) Block Sharding (块分片)：将数据分片并交替存储在多个磁盘上。给每个磁盘都分配一个预取线程用于将该磁盘内的数据预取进内存缓冲区 (in-memory buffer)，这样训练线程就可以交替地从每个 buffer 中读取数据

Discussion

• Ref: 为啥 Xgboost 比 Gradient Boost 好那么多？

---

• 可扩展性 (scalability): The system runs more than ten times faster than existing popular solutions on a single machine and scales to billions of examples in distributed or memory-limited settings. The scalability of XGBoost is due to several important systems and algorithmic optimizations:
  • 用于处理稀疏数据的 Sparsity-aware Split Finding
  • 基于 weighted quantile sketch 的 approximate tree learning
  • 支持并行和分布式计算
  • 支持核外计算 (Out-of-core Computation)，在单机上也能处理大型数据集
• 为什么 XGboost 比 GBDT 更好？
  • 在目标函数中加入正则项，同时使用 Shrinkage 和 Column subsampling 来防止过拟合
  • Sparsity-aware Split Finding 使得 XGboost 能高效处理缺失值，而 GBDT 则没有对缺失值作特殊处理
  • XGboost 的可扩展性 (scalability) (即 scalability 中总结的四点)
  • GBDT 在优化时只用到一阶导数信息，XGboost 则对代价函数进行了二阶泰勒展开，同时用到了一阶和二阶导数
  • GBDT 以 CART 回归树作为基分类器，XGboost 不仅支持 CART 回归树，还支持线性分类器，这个时候 XGboost 相当于带 L1 和 L2 正则化项的 logistic 回归 (分类问题) 或者线性回归 (回归问题) (这点似乎没在论文里看到？)

XGBoost 库

• Ref: 机器学习算法之 XGBoost

---

Useful Links

• XGBoost package (GitHub): https://github.com/dmlc/xgboost
  • The distributed version is built on top of the rabit library for allreduce. The distributed XGBoost runs natively on Hadoop, MPI Sun Grid engine. Recently, we also enable distributed XGBoost on jvm bigdata stacks such as Flink and Spark. The distributed version has also been integrated into cloud platform Tianchi of Alibaba.
• XGBoost Tutorial

LightGBM

Ref

• paper: LightGBM: A Highly Efficient Gradient Boosting Decision Tree
• 深入理解 LightGBM
• 详解 LightGBM 两大利器：基于梯度的单边采样（GOSS）和互斥特征捆绑（EFB）

LightGBM

• LightGBM 是一个实现 GBDT 算法的框架，支持高效率的并行训练，并且具有更快的训练速度、更低的内存消耗、更好的准确率、支持分布式可以快速处理海量数据等优点

---

Why LightGBM?

• GBDT 在寻找最佳分裂点时采用 pre-sorted 算法，对每个特征都需要遍历一次训练样本，因此计算的时间复杂度正比于特征维数和训练样本的数量。当处理大数据时 (特征维度大、训练样本多)，就会带来巨大的计算开销。因此很自然的想法就是想办法减少训练样本数和特征维数
• 同时为了更好地处理大数据，LightGBM 也支持分布式训练

---

XGBoost v.s. LightGBM

• XGBoost 的缺点：首先，空间消耗大。由于 XGBoost 对数据进行了预排序，因此不仅需要保存数据的属性值，还需要保存排序后的索引，这就需要消耗训练数据两倍的内存。其次，时间上也有较大的开销，在遍历每一个分割点的时候，都需要进行分裂增益的计算，消耗的代价大。最后，在每一层长树的时候，需要随机访问一个行索引到叶子索引的数组，并且不同特征访问的顺序也不一样，也会造成较大的 cache miss
• LightGBM 的优化：
  • 基于 Histogram 的决策树算法：通过将连续属性离散化来降低内存和计算开销
  • 单边梯度采样 Gradient-based One-Side Sampling (GOSS)：使用 GOSS 可以减少大量只具有小梯度的数据实例，这样在计算分裂增益的时候只利用剩下的具有高梯度的数据就可以了，相比 XGBoost 遍历所有属性值节省了不少时间和空间上的开销
  • 互斥特征捆绑 Exclusive Feature Bundling (EFB)：使用 EFB 可以将许多互斥的特征绑定为一个特征，这样达到了降维的目的
  • 带深度限制的 Leaf-wise 的叶子生长策略：大多数GBDT工具使用低效的按层生长 (level-wise) 的决策树生长策略，因为它不加区分的对待同一层的叶子，带来了很多没必要的开销。实际上很多叶子的分裂增益较低，没必要进行搜索和分裂。LightGBM 使用了带有深度限制的按叶子生长 (leaf-wise) 算法
  • 直接支持类别特征 (Categorical Feature)
  • 支持高效并行
  • Cache 命中率优化

LightGBM 的基本原理

基于 Histogram 的决策树算法

直方图算法

• (1) 首先确定对于每一个特征需要多少个箱子 (bin) 并为每一个箱子分配一个整数；然后将浮点数的范围均分成若干区间，区间个数与箱子个数相等，将属于该箱子的样本数据更新为箱子的值 (连续数据离散化)；最后用直方图 (#bins) 表示
  

• (2) 在遍历数据的时候，根据离散化后的值作为索引在直方图中累积统计量，当遍历一次数据后，直方图累积了需要的统计量，然后根据直方图的离散值，遍历寻找最优的分割点

• 下面给出在 level-wise 的树生长策略下，使用 histogram-based 算法训练一棵决策树的伪代码：
  

---

处理零值特征

• XGBoost 在进行预排序时只考虑非零值进行加速，而 LightGBM 也采用类似策略：只用非零特征值构建直方图，因此可以预先为每个特征准备一张表用于存储非零值，这样为一个特征建立直方图的时间复杂度就由 $O(\#data)$ 变味了 $O(\#non\_zero\_data)$
• 但这个方法会带来额外的内存开销

---

直方图算法的优势

• 我们知道特征离散化具有很多优点，如存储方便、运算更快、鲁棒性强、模型更加稳定等。对于直方图算法来说最直接的有以下两个优点：
  • 内存占用更小：直方图算法不仅不需要额外存储预排序的结果，而且可以只保存特征离散化后的值，而这个值一般用 8 位整型存储就足够了
  • 计算代价更小：预排序算法 XGBoost 每遍历一个特征值就需要计算一次分裂的增益，而直方图算法 LightGBM 只需要计算 $\#bins$ 次 ($\#bins\ll \#data$)，直接将寻找一次最佳分裂点的时间复杂度从 $O(\#data\times \#features)$ 降低到 $O(\#bins\times \#features)$ (不考虑缺失值)
• 当然，Histogram 算法并不是完美的。由于特征被离散化后，找到的并不是很精确的分割点，所以会对结果产生影响。但在不同的数据集上的结果表明，离散化的分割点对最终的精度影响并不是很大，甚至有时候会更好一点。原因是决策树本来就是弱模型，分割点是不是精确并不是太重要；较粗的分割点也有正则化的效果，可以有效地防止过拟合；即使单棵树的训练误差比精确分割的算法稍大，但在梯度提升 (Gradient Boosting) 的框架下没有太大的影响

---

直方图做差加速

• 一个叶子的直方图可以由它的父亲节点的直方图与它兄弟的直方图做差得到，在速度上可以提升一倍。通常构造直方图时，需要遍历该叶子上的所有数据，但直方图做差仅需遍历直方图的 $\#bins$ 个桶
  
• 在实际构建树的过程中，LightGBM 还可以先计算直方图小的叶子节点，然后利用直方图做差来获得直方图大的叶子节点 (直方图大的叶子结点指的就是含有样本数更多的叶结点)，这样就可以用非常微小的代价得到它兄弟叶子的直方图

带深度限制的 Leaf-wise 算法

• 大多数 GBDT 工具使用按层生长 (level-wise) 的决策树生长策略，但 Level-wise 是一种低效的算法，因为它不加区分的对待同一层的叶子，实际上很多叶子的分裂增益较低，没必要进行搜索和分裂，因此带来了很多没必要的计算开销
  
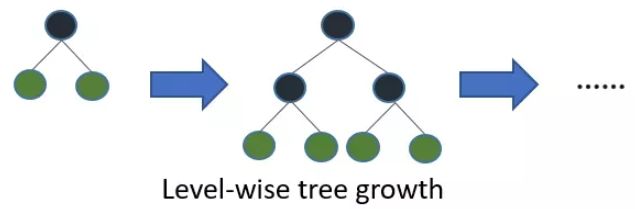
• LightGBM 抛弃了 level-wise 而使用了带有深度限制的按叶子生长 (leaf-wise) 增长策略。该策略每次从当前所有叶子中，找到分裂增益最大的一个叶子，然后分裂，如此循环。因此同 Level-wise 相比，Leaf-wise 的优点是：在分裂次数相同的情况下，Leaf-wise 可以降低更多的误差，得到更好的精度；Leaf-wise 的缺点是：可能会长出比较深的决策树，产生过拟合。因此 LightGBM 会在 Leaf-wise 之上增加了一个最大深度的限制，在保证高效率的同时防止过拟合
  

单边梯度采样算法 (GOSS)

Gradient-based One-Side Sampling

• GOSS 算法从减少样本的角度出发，排除大部分小梯度的样本 (梯度小的样本，训练误差也比较小，说明数据已经被模型学习得很好了)，仅用剩下的样本计算分裂增益，它是一种在减少数据量和保证精度上平衡的算法
• 如果直接将所有梯度较小的数据都丢弃掉势必会影响数据的总体分布。所以，GOSS 首先将要进行分裂的特征的所有取值按照梯度绝对值大小降序排序 (XGBoost 也进行了排序，但是 LightGBM 不用保存排序后的结果)，选取绝对值最大的 $a\times 100\%$ 个数据。然后在剩下的较小梯度数据中随机选择 $b\times 100\%$ 个数据。接着将这 $b\times 100\%$ 个数据梯度乘以一个常数 $\frac{1-a}{b}$ 来尽量维持梯度分布，这样算法就会更关注训练不足的样本，而不会过多改变原数据集的分布。最后使用这 $(a+b)\times 100\%$ 个数据来计算分裂增益
  

$w$: 给选出的每个样本分配权重，其中小梯度样本权重要乘上 $\frac{1-a}{b}$ 以维持梯度分布

互斥特征捆绑算法 (EFB)

Exclusive Feature Bundling

• 高维度的数据往往是稀疏的，这种稀疏性启发我们设计一种无损的方法来减少特征的维度。通常被捆绑的特征都是互斥的 (即特征不会同时为非零值，像 one-hot)，这样两个特征捆绑起来才不会丢失信息。如果两个特征并不是完全互斥 (部分情况下两个特征都是非零值)，可以用一个指标对特征不互斥程度进行衡量，称之为冲突比率，当这个值较小时，我们可以选择把不完全互斥的两个特征捆绑，而不影响最后的精度
  • 如果将一些特征进行融合绑定，则构建直方图时的时间复杂度从 $O(\#data\times \#feature)$ 变为 $O(\#data\times \#bundle)$，这里 $\#bundle$ 指特征融合绑定后特征包的个数，且 $\#bundle\ll \#feature$
• 针对这种想法，我们会遇到两个问题：
  • (1) 怎么判定哪些特征应该绑在一起（build bundled）？
  • (2) 怎么把特征绑为一个（merge feature）？

---

哪些特征应该绑在一起

• LightGBM 的 EFB 算法将绑定相互独立特征的问题转化为图着色的问题来求解，将所有的特征视为图的各个顶点，将不互斥的特征用一条边连接起来，边的权重就是两个相连接的特征的总冲突值，这样需要绑定的特征就是在图着色问题中要涂上同一种颜色的那些点 (特征)。由此可见，决定哪些特征应该绑在一起的问题是一个 NP-hard 问题，因此只能用一种近似的贪心算法来解决图着色这个 NP-hard 问题
• 同时我们注意到通常有很多特征，尽管不是 100％ 相互排斥，但也很少同时取非零值。 如果我们的算法可以允许一小部分的冲突，我们可以得到更少的特征包，进一步提高计算效率。假设每个 bundle 中的最大冲突率为 $\gamma$，则随机污染一部分特征值给训练精度带来的影响最多只有 $O([(1-\gamma )n{]}^{-2/3})$，因此只要选取一个相对小的最大冲突率，就能在精度和效率之间取得一个很好的平衡
• 具体步骤可以总结如下：
  • (1) 构造一个加权无向图 (图用邻接矩阵表示)，顶点是特征，对于不互斥的特征进行相连 (存在两个特征同时不为 0 的样本)，特征同时不为 0 的样本个数作为边的权重
  • (2) 根据节点的度进行降序排序，度越大，与其它特征的冲突越大，也就越不可能与其他特征进行捆绑
  • (3) 设置最大冲突阈值 $K$，外层循环先对每一个上述排序好的特征，遍历已有的特征捆绑簇，如果发现该特征加入到该特征簇中的冲突数不会超过最大阈值 $K$，则将该特征加入到该簇中。否则新建一个特征簇，将该特征加入到新建的簇中

• 改进算法 3：上面时间的复杂度为 $O(\#feature{s}^2)$，时间其实主要花费在建图上面，两两特征计算互斥程度的时间较长。对于百万维度的特征来说，该复杂度仍是不可行的。为了提高效率，可以不再构建图，而是直接将特征按照非零值个数排序，将特征非零值个数类比为节点的度 (即冲突程度)，因为更多的非零值更容易引起冲突。只是改进了排序策略，不再构建图，其余的算法步骤与算法 3 是一样的

这个时间复杂度 $O(\#feature{s}^2)$ 是怎么来的？如果要计算边权的话，时间复杂度的式子里怎么也应该有 $\#data$ 啊… 感觉这个 $O(\#feature{s}^2)$ 可能说的是时间复杂度的下界

---

怎么把特征绑为一捆

• 特征合并算法，其关键在于原始特征能从合并的特征中分离出来。绑定几个特征在同一个 bundle 里需要保证绑定前的原始特征的值可以在 bundle 中识别，这可以通过在特征值中加一个偏置常量来解决
  • 比如，我们在 bundle 中绑定了两个特征 $A$ 和 $B$，$A$ 特征的原始取值为区间 $[0,10)$，$B$ 特征的原始取值为区间 $[0,20)$，我们可以在 $B$ 特征的取值上加一个偏置常量 10，将其取值范围变为 $[10,30)$，绑定后的特征取值范围为 $[0,30)$，这样就可以放心地融合特征 $A$ 和 $B$ 了
• 考虑到 histogram-based 算法将连续的属性值保存为离散的 bins，这使得绑定特征更加方便了，我们可以使得同一个 bundle 中的互斥特征分到 bundle 对应直方图的不同 bin 中
  

$binRanges$ 即为 $offset$; $f.numBin$ 表示该特征分了几个 bin；$newBin[i]$ 记录第 $i$ 个样本在捆绑特征的第几个 bin 中；$F[j].bin[i]$ 表示样本 $i$ 在属性 $j$ 的第几个 bin 中

LightGBM 的工程优化

• paper: A communication-efficient parallel algorithm for decision tree

直接支持类别特征

• 实际上大多数机器学习工具都无法直接支持类别特征，一般需要把类别特征，通过 one-hot 编码，转化到多维的 0/1 特征，降低了空间和时间的效率。但我们知道对于决策树来说并不推荐使用 one-hot 编码，尤其当类别特征中类别个数很多的情况下，会存在以下问题：
  • (1) 会产生样本切分不平衡问题，导致切分增益非常小 (即浪费了这个特征)。使用 one-hot 编码，意味着在每一个决策节点上只能使用 one vs rest（例如是不是狗，是不是猫等）的切分方式。例如，动物类别切分后，会产生是否狗，是否猫等一系列特征，这一系列特征上只有少量样本为 1，大量样本为 0，这时候切分样本会产生不平衡，这意味着切分增益也会很小。较小的那个切分样本集，它占总样本的比例太小，无论增益多大，乘以该比例之后几乎可以忽略；较大的那个拆分样本集，它几乎就是原始的样本集，增益几乎为零。比较直观的理解就是不平衡的切分和不切分没有区别
  • (2) 会影响决策树的学习。因为就算可以对这个类别特征进行切分，独热编码也会把数据切分到很多零散的小空间上，如下图左边所示。而决策树学习时利用的是统计信息，在这些数据量小的空间上，统计信息不准确，学习效果会变差。但如果使用下图右边的 many vs. many 的切分方法，数据会被切分到两个比较大的空间，进一步的学习也会更好。下图右边叶子节点的含义是 $X=A$ 或者 $X=C$ 放到左孩子，其余放到右孩子
    
• 为了解决 one-hot 编码处理类别特征的不足，LightGBM 优化了对类别特征的支持，可以直接输入类别特征，不需要额外的 0/1 展开。LightGBM 采用 many-vs-many 的切分方式将类别特征分为两个子集，实现类别特征的最优切分。假设某维特征有 $k$ 个类别，则朴素的枚举算法需要枚举 $2^{k-1}-1$ 种可能，时间复杂度为 $O(2^k)$，LightGBM 基于 Fisher 的 $On$ $Grouping$ $For$ $Maximum$ $Homogeneity$ 论文实现了 $O(k\log k)$ 的时间复杂度
  • 算法流程：对类别属性建立直方图，其中每个类别都对应一个 bin，然后将 bin 按照 $sum\_gradient/sum\_hessian$ 的值进行排序，之后找最佳分裂点的过程与数值类型的处理一致
  • LightGBM 的作者在知乎上的回答中说的排序标准为每一类的标签平均值 $avg(y)=\frac{Sum(y)}{Count(y)}$，算法流程如下图所示；但官方文档中的排序标准却是 $sum\_gradient/sum\_hessian$，而且我目前还不明白为什么要按照 $sum\_gradient/sum\_hessian$ 进行排序…
    

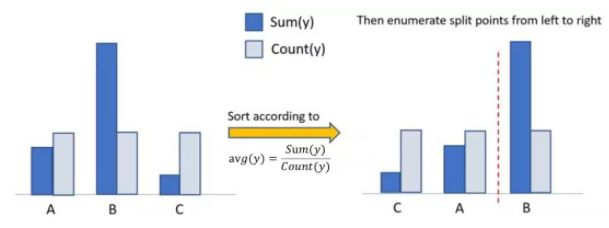
支持高效并行

特征并行 (Feature Parallel)

• 特征并行的主要思想是不同机器在不同的特征集合上分别寻找最优的分割点 (local best split)，然后与其他机器通信来找到全局最优分割点 (global best split)。但由于进行了数据的垂直划分，每台机器只有样本的一部分属性，因此只有对应全局最优分割点的机器才能执行分割，然后将分割结果传输给其他机器，最后其他机器才能根据得到的分割结果对本地数据进行分割。XGBoost 使用的就是这种特征并行方法。可以看出，这种实现方法会带来很大的通信开销 (需要额外传输分割结果，每个样本大约需要传输 1 位数据，总共需要传输 $\#data/8$ byte) 以及计算开销 (因为没有找到全局最优分割点的机器还需要等待接收到分割结果后才能进行分割，一次分割的时间开销为 $O(\#data)$)
  
• LightGBM 则不进行数据垂直划分，而是在每台机器上保存全部训练数据，在得到全局最佳分割点后就可在本地执行分割，大大降低了时间开销

---

数据并行 (Data Parallel)

• 传统的数据并行策略主要为水平划分数据，让不同的机器先在本地构造所有特征的直方图，然后进行全局的合并，最后在合并的直方图上面寻找最优分割点。这种数据划分有一个很大的缺点：通讯开销过大。如果使用点对点通信，一台机器的通讯开销大约为 $O(\#machine\times \#features\times \#bin)$；如果使用集成的通信，则通讯开销为 $O(2\times \#features\times \#bin)$
  
• LightGBM 在数据并行中使用分散规约 (Reduce scatter) 把合并不同特征直方图的任务分摊到不同机器上，然后这些机器在自己合并完的一部分特征直方图 (local merged histogram) 中找出局部最佳分裂点 (local best split)，然后再由所有的局部最佳分裂点找出全局最佳分裂点 (global best split)
• 除此之外，LightGBM 还利用了直方图做差，在计算直方图时，只需要计算一个叶结点的直方图，然后通过做差来得到它兄弟结点的直方图

---

投票并行 (Voting Parallel)

• 基于投票的数据并行则进一步优化数据并行中的通信代价，使其变成常数级别。大致步骤为三步：
  • (1) Local Voting: 每台机器都根据本地数据集找出最佳的 $k$ 个用于分裂的属性，然后和其他机器交换选出的 $k$ 个最佳属性的索引，通信开销仅为 $O(k\times \#machine)$
  • (2) Global Voting: 在得到所有机器上选出的局部最佳属性索引后，计算出每个属性被选择的次数并按照降序排序，然后选择前 $2k$ 个属性 (也就是多数表决法)。这一步没有通信开销
  • (3) Best Attribute Identification: 合并上一步选出的 $2k$ 个属性的局部直方图，得到全局直方图，然后从中选出最佳分裂属性和最佳分裂点，通讯开销仅为 $O(\#machine\times 2k\times \#bin)$
    
• 在使用投票并行后，LightGBM 的通信开销已经独立于特征维数以及样本数，极大地增加了它的可扩展性

可以被证明，Voting Parallel 可以有很大几率找到最优分裂点，并且该几率随着训练样本数的增加而趋近于 1 (与 $k$ 无关)，具体的理论验证可参见 A communication-efficient parallel algorithm for decision tree

Cache 命中率优化

• XGBoost 对 cache 优化不友好，如下图所示。在预排序后，特征对梯度的访问是一种随机访问，并且不同的特征访问的顺序不一样，会造成较多的 Cache miss。同时，在每一层长树的时候，需要随机访问一个行索引到叶子索引的数组，并且不同特征访问的顺序也不一样，也会造成较大的 cache miss
  

---

• LightGBM 使用的直方图算法对 Cache 天生友好：
  • (1) 首先，所有的特征都采用相同的方式获得梯度 (区别于 XGBoost 的不同特征通过不同的索引获得梯度)，只需要对梯度进行排序并可实现连续访问，大大提高了缓存命中率
  • (2) 其次，因为不需要存储行索引到叶子索引的数组，降低了存储消耗，而且也不存在 Cache Miss 的问题
    

LightGBM 的优缺点

优点

这部分主要总结下 LightGBM 相对于 XGBoost 的优点

• (1) 速度更快
  • LightGBM 采用了直方图算法将遍历样本转变为遍历直方图，极大的降低了时间复杂度
  • LightGBM 在训练过程中采用单边梯度算法过滤掉梯度小的样本，减少了大量的计算
  • LightGBM 采用了基于 Leaf-wise 算法的增长策略构建树，减少了很多不必要的计算量
  • LightGBM 采用优化后的特征并行、数据并行方法加速计算，当数据量非常大的时候还可以采用投票并行的策略
  • LightGBM 对缓存也进行了优化，增加了缓存命中率
• (2) 占用内存更小
  • XGBoost 使用预排序后需要记录特征值及其对应样本的统计值的索引，而 LightGBM 使用了直方图算法将特征值转变为 bin 值，且不需要记录特征到样本的索引，将空间复杂度从 $O(2\times \#data)$ 降低为 $O(\#bin)$，极大的减少了内存消耗
  • LightGBM 在训练过程中采用互斥特征捆绑算法减少了特征数量，降低了内存消耗

---

缺点

• 可能会长出比较深的决策树，产生过拟合。因此 LightGBM 在 Leaf-wise 之上增加了一个最大深度限制，在保证高效率的同时防止过拟合
• Boosting 族是迭代算法，每一次迭代都根据上一次迭代的预测结果对样本进行权重调整，所以随着迭代不断进行，误差会越来越小，模型的偏差会不断降低。由于 LightGBM 是基于偏差的算法，所以会对噪点较为敏感
• 在寻找最优解时，依据的是最优切分变量，没有将最优解是全部特征的综合这一理念考虑进去

Discussion

LightGBM 与 XGBoost 的联系和区别有哪些？

• (1) LightGBM 使用了基于 histogram 的决策树算法，这一点不同于 XGBoost 中的贪心算法和近似算法，histogram 算法在内存和计算代价上都有不小优势。1) 内存上优势：很明显，直方图算法的内存消耗为 $(\#data\times \#features\times 1Bytes)$ (因为对特征分桶后只需保存特征离散化之后的值)，而 XGBoost 的贪心算法内存消耗为：$2\times \#data\times \#features\times 4Bytes$，因为 XGBoost 既要保存原始 feature 的值，也要保存这个值的顺序索引，这些值需要 32 位的浮点数来保存。2）计算上的优势：预排序算法在选择好分裂特征计算分裂收益时需要遍历所有样本的特征值，时间为 $O(\#data\times \#feature)$，而直方图算法只需要遍历桶就行了，时间为 $O(\#bin\times \#feature)$
• (2) XGBoost 采用的是 level-wise 的分裂策略，而 LightGBM 采用了 leaf-wise 的策略，区别是 XGBoost 对每一层所有节点做无差别分裂，可能有些节点的增益非常小，对结果影响不大，但是 XGBoost 也进行了分裂，带来了不必要的开销。leaft-wise 的做法是在当前所有叶子节点中选择分裂收益最大的节点进行分裂，如此递归进行，很明显 leaf-wise 这种做法容易过拟合，因为容易陷入比较高的深度中，因此需要对最大深度做限制，从而避免过拟合
• (3) XGBoost 在每一层都动态构建直方图 (XGBoost 也实现了 histogram 算法，比原来 presorted 算法快了不少。但相比 LightGBM，还是慢了一些，且内存占用还是比较大；还没有看过 XGBoost 的直方图算法，以后看)，因为 XGBoost 的直方图算法不是针对某个特定的特征，而是所有特征共享一个直方图 (每个样本的权重是二阶导)，所以每一层都要重新构建直方图，而 LightGBM 中对每个特征都有一个直方图，所以构建一次直方图就够了 (为什么呢？难道不是每次分裂出新结点都需要重新计算该结点的直方图？)
• (4) LightGBM 使用直方图做差加速，一个子节点的直方图可以通过父节点的直方图减去兄弟节点的直方图得到，从而加速计算
• (5) LightGBM 支持类别特征，不需要进行独热编码处理
• (6) LightGBM 优化了特征并行和数据并行算法，除此之外还添加了投票并行方案
• (7) LightGBM 采用基于梯度的单边采样来减少训练样本并保持数据分布不变，减少模型因数据分布发生变化而造成的模型精度下降
• (8) 特征捆绑转化为图着色问题，减少特征数量

LightGBM 库

Useful Links

• LightGBM Package (GitHub): https://github.com/Microsoft/LightGBM
• 深入理解 LightGBM: LightGBM 实例一节
• LightGBM 源码阅读+理论分析（处理特征类别，缺省值的实现细节）
• LightGBM Tutorial