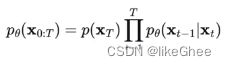（pytorch进阶之路）DDPM扩散概率模型

概述

扩散概率模型
《deep unsupervised learning using nonequilibrium thermodynamics》
https://arxiv.org/pdf/1503.03585.pdf
《denoising diffusion probabilistic models》
2020年
https://arxiv.org/pdf/2006.11239.pdf

类似VAE GAN是一个生成式模型

生成模型一共五类，
seq2seq自回归的解码
GAN，通过判别器迭代优化生成器
Flow，数学严谨可逆过程，设计巧妙的结构
VAE，
Diffusion model，

前置知识

条件概率公式，比较简单可以见贝叶斯公式
P(ABC) = P(C|BA) P(BA) = P(C|BA) P(B|A) P(A)
P(BC|A) = P(B|A) P(C|AB) (两边同乘P(A)推导)
基于马尔可夫链的条件概率
A->B->C，当前选择只受到前一次的结果以及对应转移概率的影响，与在之前的选择无关
无记忆性 P(St| St-1 St-2 …) = P(St|St-1)
P(ABC) = P(C|BA)(BA) = P(C|B) P(B|A) P(A)
P(BC|A) = P(B|A) P(C|B)

高斯分布的KL散度公式
KL散度 = （ - 信息熵）+（交叉熵）
KL散度（距离）一般被用于计算两个分布之间的不同，KL距离并不是对称的
对于两个单一变量的高斯分布p和q而言，它们的KL散度为

信息量：指一个时间所能带来的信息的多少，一般地这个事件发生概率越小，所能带来的信息量越大
I = -log2(p(x))

信息熵：一个概率分布p的平均信息量，代表着随机变量或系统的不确定性，熵越大，随机变量或系统的不确定性就越大
H§ = -∑p(x)·log2(p(x))
交叉熵
H(A,B) = - ∑ Pa(xi) [log Pb(xi)]

参数重整化
若希望从高斯分布N（μ，σ2）中采样，可以先从标准分布N（0,1) 采样出z， 再得到 σ×z+μ，如果我们直接采样N（μ，σ2），假设μ和σ是通过神经网络预测出来的，导致μ和σ和采样出来的结果断开了，梯度无法传导了，因为采样过程是不可导的，为了仍然是梯度可更新的，从标准分布中采样出z，经过缩放和平移得到采样值，z可以看作是网络输入或者是常数，那么采样值μ和σ就是完全可导的

---

VAE，我们认为x是由某个隐变量z生成的，z通过后验网络输入x生成，在推理的时候从z预测x

公式：首先是p(x)公式，接着公式两边同时乘以后验网络qΦ(z|x)，已知x去预测z，两边取log，右边写成期望值形式，最后通过jensen不等式，将log移到期望值里面，得到最后的目标数据分布的下界，最大化下界则转为最大化期望值的式子，

多层VAE，z2生成z1，z1生成x，那么px就可以写成联合概率分布，对z1和z2分别积分，同样的分子分母同乘一个qΦ，再写成期望的形式

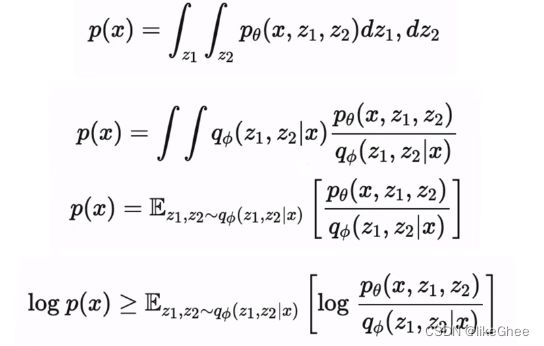
使用马尔科夫链的条件概率，带入，写成最后的对数似然的下界，这就是多层VAE的下界

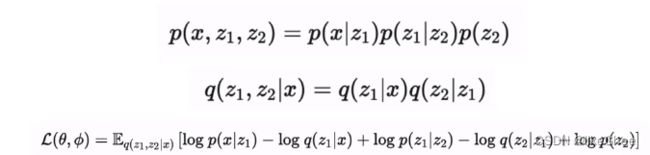
这个过程和Diffuision model很类似，diffusion也是从目标分布中x0加噪逐渐生成一个最终的分布xT，推理从xT得到x0，diffusion和vae的目标函数十分相似

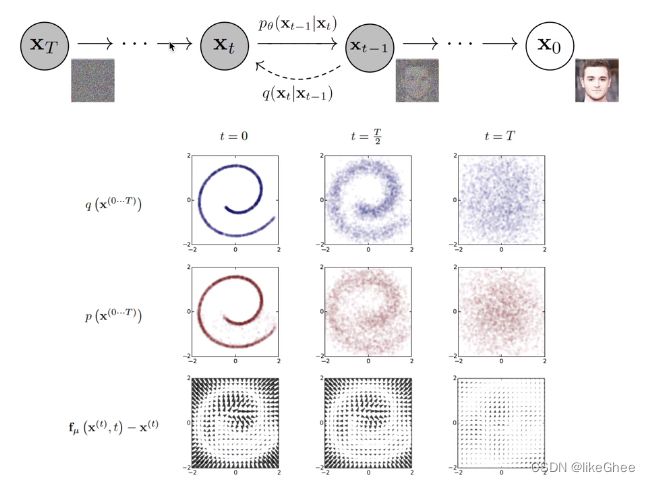
diffusion图示

两个过程，有序变到无序过程称为扩散过程， 逆扩散过程则是从噪声分布逐步预测出目标的分布

第三行可以看作reverse过程中每个像素点的位置相比最右边高斯分布时候的偏移量

扩散过程

给定初始数据分布x0~q（x），可以不断地向分布中添加高斯噪声（不含参的，是确定值的），该噪声的标准差以固定值βt而确定的，均值是以固定值βt和当前时刻t的数据xt决定的，这个过程是一个马尔科夫链过程

随着t的不断增大，最终数据分布xT变成了一个各向独立的高斯分布

xt-1去预测xt是一个高斯分布，并且均值和方差由β和当前时刻的x确定
q(xt|xt-1) = N(xt; 根号下1-βt × xt-1， βt·I)
I是单位矩阵

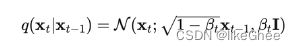
那么联合概率为
任何时刻的q(xt)可以直接基于x0和βt计算出来，而不需要迭代

用参数重整化可以推导：

最终q(xt|x0)变为了各向同性的高斯分布，就可以算出α-t在任意时候符合一个标准的分布了

βt越来越大，xT和x0是同一个维度的

逆扩散过程

从高斯分布中恢复原始模型
我们假设从xt逐步恢复到x0是一个高斯分布，并且逆扩散过程仍然是马尔科夫链过程
构建一个网络去估计，从xt预测xt-1 服从 N（xt-1；μθ（xt，t），Σθ（xt，t）），xt和t作为输入，含参的正太分布

则联合概率密度分布为

后验的扩散条件概率

后验的扩散条件概率q（xt-1|xt，x0）分布是可以用公式表达的，给定xt和x0是可以计算出xt-1的

高斯分布概率密度函数

注意公式：

根据贝叶斯公式推导：

根据x0和xt之间的关系，将x0的表达式代入到q（xt-1|xt，x0）的分布中，可以重新给出该分布的均值表达式，这个时候表达式不再含有x0，并且多了噪声项，这为后面设计神经网络提供了基础，在x0的条件下，后验条件高斯分布的均值只与xt和zt有关，zt是t时刻的随机正态分布变量，源自参数重整化

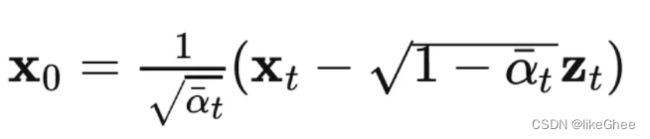
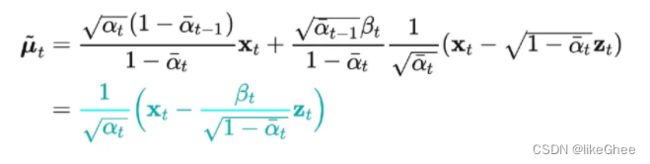
似然函数

负对数似然加上KL散度，KL散度对于等于0，获得上界，上界取最小，负对数似然小于最小值


在上式中，L0在DDPM原论文中由于选择了固定方差，LT为常数，而L0相当于从连续空间到离散空间的解码loss，仿照VAE的做法，将连续的高斯分布转换成离散的分布

算法

训练：从q（x0）中采样数据，等价于从数据集中拿出一部分数据，同时随机地生成一个时刻t，再随机地生成一个正态分布的噪声epsilon（ε），将这些量带入目标函数中，进行最小化
εθ是一个网络，喂入x0，αt，t，从网络中随机生成一个ε噪声，网络算出一个新的和x0一样维度的东西，再和网络中生成的ε做差
关于预测，其实可以预测x0，也可以预测噪音，也可以预测期望值。DDPM中选择了预测噪音，所以重参数化那里就选择了将噪音作为含参网络的预测目标。

右边是采样：一旦优化好了εθ网络，完全可以从xt推出xt-1，xt-2，…，x0，从t到1迭代，生成z的目的是为了采样，正态分布中采样一个z，乘以方差加上均值，得到当前的分布的采样值xt-1，t次采样后得到x0

代码实现

选择一个数据集，用sklearn的s_curve，将散点图画出来就是一个S，通过make_s_curve函数生成一万个点，每个点只取第0维和第2维，s_curve的形状是[10000, 2]， 把它构建成一个张量，变成float类型，作为训练集

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_s_curve
import torch

s_curve,_ = make_s_curve(10**4,noise=0.1)
s_curve = s_curve[:,[0,2]]/10.0

print("shape of s:",np.shape(s_curve))

data = s_curve.T

fig,ax = plt.subplots()
ax.scatter(*data,color='blue',edgecolor='white');

ax.axis('off')

dataset = torch.Tensor(s_curve).float()

---

确定超参数的值，步骤设为100，确定每一步的β值，sigmoid函数递增

α等于1-β
α_prod是把整个α连乘
α_prod_previous只取α_prod的第一项开始，第0项设为1
α_bar_sqrt是α_prod的开根号
一减去α bar log，还有一减去α bar sqrt等等

形状大小都是一样的[100]，这些值是超参数，不需要训练的

num_steps = 100

#制定每一步的beta
betas = torch.linspace(-6,6,num_steps)
betas = torch.sigmoid(betas)*(0.5e-2 - 1e-5)+1e-5

#计算alpha、alpha_prod、alpha_prod_previous、alpha_bar_sqrt等变量的值
alphas = 1-betas
alphas_prod = torch.cumprod(alphas,0)
alphas_prod_p = torch.cat([torch.tensor([1]).float(),alphas_prod[:-1]],0)
alphas_bar_sqrt = torch.sqrt(alphas_prod)
one_minus_alphas_bar_log = torch.log(1 - alphas_prod)
one_minus_alphas_bar_sqrt = torch.sqrt(1 - alphas_prod)

assert alphas.shape==alphas_prod.shape==alphas_prod_p.shape==\
alphas_bar_sqrt.shape==one_minus_alphas_bar_log.shape\
==one_minus_alphas_bar_sqrt.shape
print("all the same shape",betas.shape)

---

确定扩散过程任意时刻的采样值
计算q（xt|x0）公式，给定初始的训练数据分布，算出任意时刻xt的采样值

公式只和x0和t有关，首先生成正态分布的随机 噪声noise，得到均值和方差，使用重整化技巧，噪声乘以标准差alphas_1_m_t，加上一个均值alphas_t * x_0

#计算任意时刻的x采样值，基于x_0和重参数化
def q_x(x_0,t):
    """可以基于x[0]得到任意时刻t的x[t]"""
    noise = torch.randn_like(x_0)
    alphas_t = alphas_bar_sqrt[t]
    alphas_1_m_t = one_minus_alphas_bar_sqrt[t]
    return (alphas_t * x_0 + alphas_1_m_t * noise)#在x[0]的基础上添加噪声
    

---

演示原始数据加噪100步，每间隔5步画出共20张图，遍历循环，传入一个时刻t，传入qx函数中算出x5的值，将图片画出来

num_shows = 20
fig,axs = plt.subplots(2,10,figsize=(28,3))
plt.rc('text',color='black')

#共有10000个点，每个点包含两个坐标
#生成100步以内每隔5步加噪声后的图像
for i in range(num_shows):
    j = i//10
    k = i%10
    q_i = q_x(dataset,torch.tensor([i*num_steps//num_shows]))#生成t时刻的采样数据
    axs[j,k].scatter(q_i[:,0],q_i[:,1],color='red',edgecolor='white')
    axs[j,k].set_axis_off()
    axs[j,k].set_title('$q(\mathbf{x}_{'+str(i*num_steps//num_shows)+'})$')

---

编写拟合逆扩散过程高斯分布的模型
模型对应εθ网络

输入的t经过embedding层，将x输入linear层和relu，输出的结果加上t_embedding，再送入relu层，每一层的embedding都是新的一个可学习的embbedding，最后输出x

十分简单的网络，完全由MLP和Relu构成

import torch
import torch.nn as nn

class MLPDiffusion(nn.Module):
    def __init__(self,n_steps,num_units=128):
        super(MLPDiffusion,self).__init__()
        
        self.linears = nn.ModuleList(
            [
                nn.Linear(2,num_units),
                nn.ReLU(),
                nn.Linear(num_units,num_units),
                nn.ReLU(),
                nn.Linear(num_units,num_units),
                nn.ReLU(),
                nn.Linear(num_units,2),
            ]
        )
        self.step_embeddings = nn.ModuleList(
            [
                nn.Embedding(n_steps,num_units),
                nn.Embedding(n_steps,num_units),
                nn.Embedding(n_steps,num_units),
            ]
        )
    def forward(self,x,t):
#         x = x_0
        for idx,embedding_layer in enumerate(self.step_embeddings):
            t_embedding = embedding_layer(t)
            x = self.linears[2*idx](x)
            x += t_embedding
            x = self.linears[2*idx+1](x)
            
        x = self.linears[-1](x)
        
        return x

---

编写训练误差函数
最简单的就是ε-εθ的MSE

对batchsize样本随机生成时刻t，t随机分散，先生成一半，另一半的t=n_steps-1-t，起到t尽量不重复的效果

t的形状[batchsize，1]，将1维度压缩掉，unsqueeze，方便我们取系数

生成噪声ε，根据均值和标准差缩放平移成model输入x，再将t输入得到输出

和噪声ε做MSE得到loss

def diffusion_loss_fn(model,x_0,alphas_bar_sqrt,one_minus_alphas_bar_sqrt,n_steps):
    """对任意时刻t进行采样计算loss"""
    batch_size = x_0.shape[0]

    #对一个batchsize样本生成随机的时刻t
    t = torch.randint(0,n_steps,size=(batch_size//2,))
    t = torch.cat([t,n_steps-1-t],dim=0)
    t = t.unsqueeze(-1)

    #x0的系数
    a = alphas_bar_sqrt[t]

    #eps的系数
    aml = one_minus_alphas_bar_sqrt[t]

    #生成随机噪音eps
    e = torch.randn_like(x_0)

    #构造模型的输入
    x = x_0*a+e*aml

    #送入模型，得到t时刻的随机噪声预测值
    output = model(x,t.squeeze(-1))

    #与真实噪声一起计算误差，求平均值
    return (e - output).square().mean()

---

逆扩散采样
p sample loop从xt中恢复 xt-1，xt-2，…， x0
p sample就是一个参数重整化的过程，根据μθ公式得到均值，方差是βt的开方

在生成正态分布的随机量z，z乘上方差加上均值得到sample

def p_sample_loop(model,shape,n_steps,betas,one_minus_alphas_bar_sqrt):
    """从x[T]恢复x[T-1]、x[T-2]|...x[0]"""
    cur_x = torch.randn(shape)
    x_seq = [cur_x]
    for i in reversed(range(n_steps)):
        cur_x = p_sample(model,cur_x,i,betas,one_minus_alphas_bar_sqrt)
        x_seq.append(cur_x)
    return x_seq

def p_sample(model,x,t,betas,one_minus_alphas_bar_sqrt):
    """从x[T]采样t时刻的重构值"""
    t = torch.tensor([t])
    
    coeff = betas[t] / one_minus_alphas_bar_sqrt[t]
    
    eps_theta = model(x,t)
    
    mean = (1/(1-betas[t]).sqrt())*(x-(coeff*eps_theta))
    
    z = torch.randn_like(x)
    sigma_t = betas[t].sqrt()
    
    sample = mean + sigma_t * z
    
    return (sample)

---

编写训练代码
构造dataloader
遍历epoch次，遍历dataloader数据集
计算loss
送入optimizer进行优化

print('Training model...')
batch_size = 128
dataloader = torch.utils.data.DataLoader(dataset,batch_size=batch_size,shuffle=True)
num_epoch = 4000
plt.rc('text',color='blue')

model = MLPDiffusion(num_steps)#输出维度是2，输入是x和step
optimizer = torch.optim.Adam(model.parameters(),lr=1e-3)

for t in range(num_epoch):
    for idx,batch_x in enumerate(dataloader):
        loss = diffusion_loss_fn(model,batch_x,alphas_bar_sqrt,one_minus_alphas_bar_sqrt,num_steps)
        optimizer.zero_grad()
        loss.backward()
        torch.nn.utils.clip_grad_norm_(model.parameters(),1.)
        optimizer.step()
        
    if(t%100==0):
        print(loss)
        x_seq = p_sample_loop(model,dataset.shape,num_steps,betas,one_minus_alphas_bar_sqrt)
        
        fig,axs = plt.subplots(1,10,figsize=(28,3))
        for i in range(1,11):
            cur_x = x_seq[i*10].detach()
            axs[i-1].scatter(cur_x[:,0],cur_x[:,1],color='red',edgecolor='white');
            axs[i-1].set_axis_off();
            axs[i-1].set_title('$q(\mathbf{x}_{'+str(i*10)+'})$')