深度学习入门：神经网络基础+多层感知机

深度学习入门：神经网络基础+多层感知机

学习过程中的一些整理。

1、神经网络基础（Artificial Neural Unit）

基于人类神经元抽象得出的数学模型


人类神经元的结构：
树突（输入）：接受别的神经元传递的信息
细胞核（处理）：处理所接收的信息
轴突、轴突末梢（输出）：将细胞核处理好的信息传递给别的神经元

M-P模型的结构：
1、对应树突（输入）
Input:接受输入数据
Weights:权重，与所接收的数据相乘(对应人工神经元中的连接强度)

2、对应细胞核（处理）
Sum(Sigma):求和操作
Threadhold:激活函数(即阈值函数，当大于一定阈值时，该函数会被激活(对应人工神经元中激活和抑制两种状态))

3、对应轴突、轴突末梢（输出）
Output:输出

表达式：

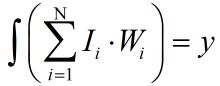
神经网络构成：由大量的神经元以某种连接方式所构成的机器学习模型。

Perception（感知机）

****表示向量乘法
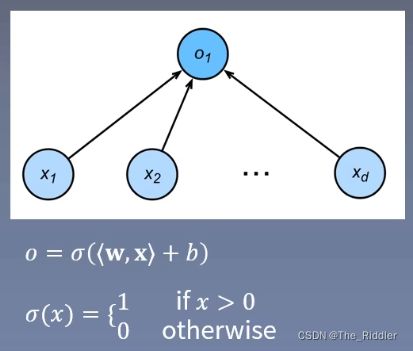
b表示偏置项(bias)（一般不会在图中绘制出）
感知机的缺点：
Perceptron不能解决异或问题。
由于Perceptron在二维平面上就是一条直线，而在二维平面中异或得出的相同结果处于对角线的位置，无法用一条直线将两种结果分隔开，所以不可能解决异或问题。
通过化简（忽略掉激活函数）得出一条直线的表达式（O不是0，是一个变量，表示输出）
最终化简为：y = kx + b ，是一条直线。
推导过程如下：

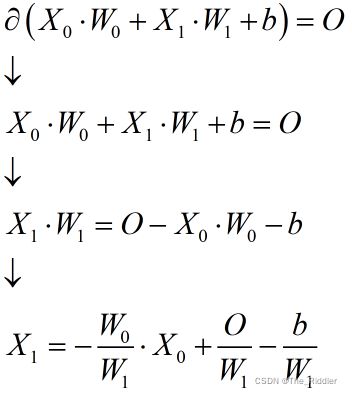
可以看出这是一条直线的表达式——一条直线当然无法解决异或问题——无法保证直线的两侧分别是同一类，说明了perceptron无法解决异或问题，这导致人工神经网络的第一次衰落。

2、多层感知机（Multi Layer Perceptron）

单层神经网络的基础上引入一个或多个隐藏层，从而使神经元有多个网络层

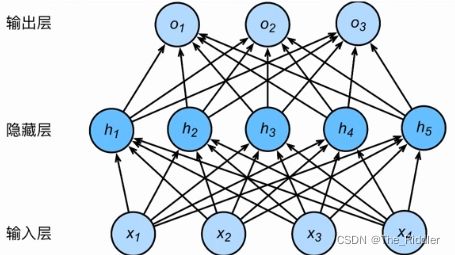
简单的多层感知机(上图):
也称为两层神经网络，因为只有两层(隐藏层和输出层)具有权重参数，在神经网络中只会计算有权重参数的层。
隐藏层权重参数通常写成W(4*5)：即输入(输入层中)有四个神经元——对应每一个神经元所连接的输入层的神经元个数——输出(隐藏层中)有五个神经元。

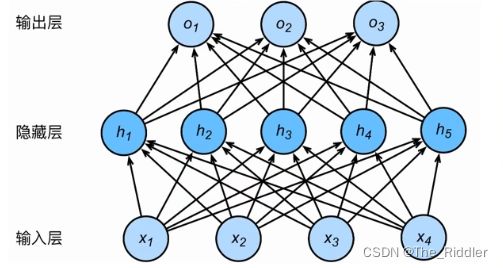
三个隐藏层的多层感知机(下图)：
规则与上图类似。

多层感知机的前向传播(Forward Propagation)

表达式：

多层感知机的激活函数
对于激活函数，推导得:

当没有激活函数时，两层的多层感知机的输出表达式可以化简为O = XW + b，即退化成了单层感知机了。
因此，在隐藏层中加入激活函数，就可以避免网络退化。

激活函数的作用：
1.让多层感知机成为真正的多层，避免网络退化等价于一层。
2.引入非线性，使网络可以逼近任意非线性函数(万能逼近定理，universal approximator:只需要一层感知机加上激活函数，就能逼近任意的非线性函数) 。

激活函数的性质：
1.连续并可导(允许少数点上不可导)，便于利用数值优化的方法来学习网络参数。
2.激活函数及其导函数要尽可能的简单，有利于提高网络计算效率。
3.激活函数的导函数的值域要在合适区间内，不能太大也不能太小，否则会影响训练的效率和稳定性。

常见的激活函数：

1.sigmoid(S型):
早期的神经网络中使用较多，现在主要在RNN神经网络中使用较多。
函数值处于0 - 1之间，符合概率值的区间，因此经常用于二分类问题中输出的激活函数，将实数变换到0到1之间符合概率分布的形式。
在RNN中也作为各种门控单元的激活函数，用来控制信息的流动(保留或者遗忘)。
饱和区域(左一黄色曲线(导函数)的两个矩形框) 。

弊端:如果神经元大量落入饱和区，其梯度几乎是0，因此无法继续向前传播梯度，更新权重，使网络模型的训练变得相对困难。

导函数计算比较方便。

2.Tanh(双曲正切)：
值域在 -1 到 1 之间，对称(0均值)
弊端:如果神经元大量落入饱和区，其梯度几乎是0，因此无法继续向前传播梯度，更新权重，使网络模型的训练变得相对困难。

3.ReLU(修正线性单元):
不存在饱和区，因此现在广泛应用于神经网络中，特别是在CNN中，隐藏层几乎不使用sigmoid和tanh作为激活函数。
导函数:在 x = 0 处没有定义(激活函数连续并可到，但允许在少数点上不可导)，可以认为 x = 0 处的导数是0或者1。
运算简单 。

激活函数的两个大类：
1.饱和激活函数:sigmoid、tanh
2.非饱和激活函数:ReLU

多层感知机的反向传播(Back Propagation)：
前向传播:输入层数据开始从前向后，数据逐步传递至输出层。
反向传播:损失函数开始从后向前，梯度逐步传递至第一层。
反向传播作用:用于权重更新，使网络输出更接近标签。
损失函数: 衡量模型输出与真实标签的差异，Loss= f(y^,y)。

反向传播原理: 微积分中的链式求导法则。

网络计算图
以一个简单的多重感知机为例

下图为它的网络计算图，
矩形框:节点，数据
圆圈:操作

公式描述：

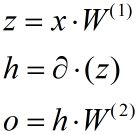
计算符定义:prod(x,y)，表示 x 与 y 根据形状做必要的变换，然后相乘(简化了矩阵运算的难度，规避了左乘与右乘的差异) 。
以上图为例，其推导过程如下：

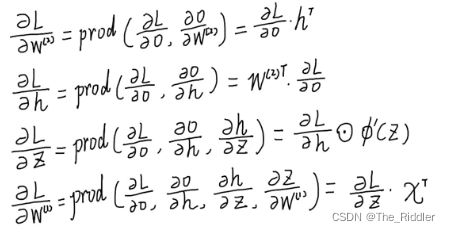
梯度下降法（Gradient Decent）

梯度下降法:权值沿梯度负方向更新，使函数值减小。
导数:函数在指定坐标轴上的变化率。
方向导数:指定方向上的变化率。
梯度:一个向量，方向为方向导数取得最大值的方向。

注：
梯度在二维空间中很好理解，就是导数。但在三维空间中，函数在一个点上面的导数往往有很多个，根据定义，只选择导数最大的作为梯度。
同时还应该注意，由于是梯度下降法，因此权值是沿着梯度的负方向更新的，使函数值减小。

学习率（Learning Rate）

学习率:用于控制、更新步长。

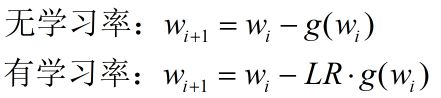
四种不同学习率下，函数优化的过程。

学习率通常是小于1的，通常是0.1、0.01、0.001 （比较小的值），在特殊情况下才会考虑使用1作为学习率。

损失函数(Loss Function)
损失函数:衡量模型输出与真实的标签之间的差距。
1、整个训练的目标就是让输出更接近真实的标签。
2、损失函数起到了一个桥梁的作用，连接了模型输出与标签。
3、y^表示模型输出，y表示标签 。

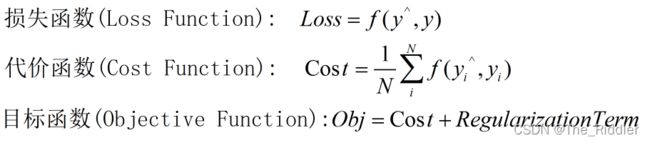
损失函数、代价函数、目标函数三者的关系:
损失函数描述的是单个样本的模型输出与标签之间的差异值。
损失函数描述的是总体样本(数据集)的模型输出与标签之间的差异值的平均值，用于观察总体的差异值，强调总体。
目标函数由两项构成:Cost(损失函数:模型输出与标签之间的差异)、Regularization Term(正则项:模型的复杂度)。
目标函数强调整个训练过程的整体目标，既要让模型的输出与标签更接近，同时不要让模型太过于复杂，太复杂容易产生过拟合现象。

两种常见的损失函数:
1、MSE(均方误差，Mean Squared Error)：
输出与标签之差的平方的均值，常在回归任务中使用。计算公式:


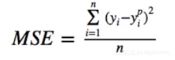
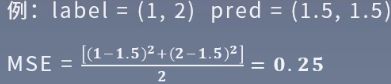
label:标签。
pred:predict，预测，表示输出值。
MSE:label和predict之间的差异值。
其在回归任务中被广泛使用.

2、CE (Cross Entropy,交叉熵)：
交叉熵源自信息论，用于衡量两个分布的差异，常在分类任务中使用。计算公式:
p:样本的真实分布
q:模型输出的概率分布
使用模型分布去逼近真实的分布，没有对称关系(p、q的位置不能交换)

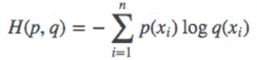
信息熵与相对熵:

信息量:某一个可能取值的自信息。
p(x):可能的取值。
信息熵用于描述信息的不确定度，信息熵越大，信息越不确定，信息熵越小，信息越确定 。

相对熵、交叉熵、信息熵之间的关系:
相对熵:衡量两个分布之间的差异(p、q同交叉熵)。
信息熵:描述信息的不确定度。
交叉熵 = 相对熵 + 信息熵。
结论:优化交叉熵等价于优化相对熵，因为信息熵是一个常数。
举例:predict是一个概率分布的形式，但是模型输出没办法保证是一个概率分布的形式，矩阵的乘法有可能得到一个负数，也可能大于1。

注：
没有一个适合所有任务的损失函数，损失函数设计会涉及算法类型、求导是否容易、数据中异常值的分布等问题。

权值初始化：
权值初始化:训练前对权值参数赋值，良好的权值初始化有利于模型训练。
简便但错误的方法:初始化为全0。
所有权值全初始化为0可能会导致的问题:会导致模型的退化，让每个网络层等价于一个神经元(不管怎么训练，所有的权重的值永远都是一样的，即等价于一个神经元)。

随机初始化法:高斯分布随机初始化，从高斯分布中随机采样，对权重进行赋值。
高斯分布：N ~ （均值，标准差）。
高斯分布的均值通常取0，以保证权重的对称性，正负值各一半。
高斯分布的标准差用来控制权重的大小，不能太大(如果太大会导致值落入饱和区，即梯度接近于0，梯度消失不利于模型的训练)，也不能太小(如果太小会使得所有的权重都为0)，大小适中。
3σ原则：99.73%数据的数据都落在(μ-3σ,μ+3σ)中间，其中μ为均值，σ为标准差。

自适应标准差
*Xavier初始化:
mean：均值
std：标准差
此时标准差会根据网络层结构的不同而改变。
a是输入神经元个数，b是输出神经元个数。

*Kaiming初始化（MSRA）:
也能根据输入神经元和输出神经元的个数来控制标准差。
代码实现上也将其称为MSRA初始化方法。

正则化方法(Regularization) :
减小方差的策略，通俗理解为减轻过拟合的策略。
误差可分解为:偏差，方差与噪声之和。即误差=偏差+方差+噪声之和。
偏差度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力。
方差度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响。
噪声则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界。

如上图
蓝色曲线：训练集准确率曲线。
橙色曲线：验证集准确率曲线。
噪声：期望泛化误差下界（任何算法所能达到的最大精度）。
偏差：刻画的是学习算法本身的拟合能力（训练集与期望泛化误差下界之间的差距）。
方差：刻画的是数据扰动带来的影响（验证集与训练集之间精度的差异）。
过拟合现象：方差过大（在训练集上表现良好，在测试集上表现糟糕），正则化就是为了解决训练集与测试集之间的精度差距。

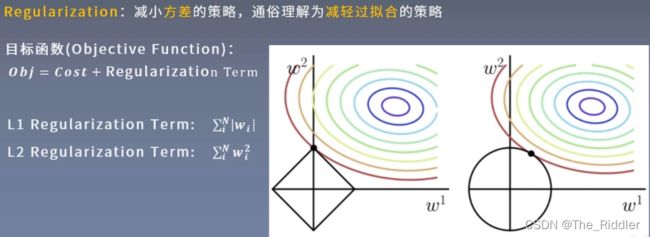L1：对所有权重的绝对值进行求和，然后作为目标函数的一项
L2：对所有权重的平方进行求和，然后作为目标函数的一项
图中彩色圆圈是Loss值的等高线：在同一等高线上，不管权重的值是多少，最终的Loss始终相等。
*理论证明：详细证明见《深度学习》（花书）第七章

正则化方法的作用：减小方差，减轻过拟合现象。

随机失活(Dropout) :
随机：以一定的概率选中神经元。
失活：失去活性，即权重变为0（不与其他神经元产生连接）。
随机失活的好处：避免网络过度地依赖某一个神经元从而实现减轻过拟合现象。
训练和测试两个阶段数据尺度的变化：在训练的时候，神经元有一定的概率被选择，从而失去活性，而在正常测试阶段失去活性的神经元会恢复活性变成正常的神经元，所有的神经元都会被使用。数据尺度的变化是由于神经元失活而丢失造成的，这样会导致模型精度的下降，所以在测试阶段，神经元的输出值要乘上神经元失活的概率P，从而使其与测试阶段的数据尺度等价。

其他的正则化方法:
Batch Normalization（BN）(现在神经网络中的标配，以下三种都是基于BN这种正则化方法在不同场景下的改进)
Layer Normalization（LN）
Instance Normalization（IN）
Group Normalization（GN）