mse均方误差计算公式_机器学习预测评价常用指标（回归：MSE,RMSE,MAE,MAPE,R2，二分类：ACC,P,R,F1,PR,ROC，多分类）...

引言：

    在我们建模的时候，我们要去选择出我们最棒的模型，就比如昨天的波士顿房价预测采用xgbt里面，我们最后需要选择出表现最好的那棵树，那怎么去评价好坏？

    这是一个回归问题，我们采用了rmse，但可以使用的评价标准还以用r2,mse,mae甚至是mape。甚至R2的评价比RMSE更客观！

cv_results = xgb.cv(...                   metrics="rmse"...)

   因此总结了回归， 分类(二分类，多分类)的常用指标，sklearn中如何导包的代码。对不同工业数据寻找模型后，找到合适指标来评价模型会有所帮助。  

【搜集的资料来源众多较为全面，欢迎大家收藏以供查阅】

★ 目录 ★

01	回归的常用指标(MSE,RMSE,MAE,MAPE,R2)
02	二分类的常用指标(acc,precision,recall,f1,PR,ROC-ACU)
03	多分类的常用指标-算法:micro,macro,weighted

一.回归的常用指标

 回归任务的评价指标：我们通过回归模型通过机器学习得到预测值，要去评价回归模型的好坏——预测值和真实之间的差别，两者之间差距肯定是越小越好。(如我预测出房价是95万元，实际房价是110万元，两者之间就有差值)

mse    均方误差

rmse   均方根误差(标准误差)

mae    平均绝对误差

mape  平均绝对百分比误差

r2_score  R方值

1.均方误差 MSE 【常用】(L2损失)

    (Mean Squared Error )

    预测值和真实值之差的平方的均值。

    可以评价数据的变化程度。

from sklearn.metrics import mean_squared_error

MSE越小越好：说明该模型描述实验数据具有更好的精度。模型之间的对比可以用其来比较。

缺点:MSE里面带着平方，会改变量纲。

    eg:若y的单位是万元，MSE计算出来的是万元的平方，对于该值，难以解释该值含义。因此产生了下面的RMSE

2.均方根误差 RMSE 【最常用】

(Root Mean Squared Error )

# sklearn中对rmse没有单独的计算，只要开方一下mse即可sqrt(mse)

    MSE的开方。(又叫标准误差)

    能够很好地反映出测量的精密度。(常用于工程测量)

RMSE越小越好

解决MSE的缺点所言：RMSE的存在是开完根号之后，误差的结果就和数据是一个单位级别的，可以更好的描述数据！

缺点：RMSE/MSE 对一组测量中对特大/特小误差反映特别敏感【对离群值，均值和标度很敏感】，这种局限性常常发生在短时间内变化比较大的数据上，如风电预测，访问量预测等

eg：

①为何对离群值敏感？

eg:比如你要预测100本书价，

模型A将99本都预测正确了，有一本预测差了10块钱，模型B将100本都预测的和真实价格差了1块钱。

得到的MSE都是一样的。那个10块钱就是离群值！是选择A还是B？按照MSE都是一样的，可实际上明显B好。

②为何对均值和标度敏感？

来看一张图：

上图：蓝点是真实值，绿线为样本均值，黄线可以预测样本趋势，但是显而易见，黄线的MSE比绿线高，哪怕其能表达样本规律，MSE上黄线就是输了！

当然，(R)MSE是最常用的回归损失函数。有解决办法:

①过滤掉这些噪声点

(当我们认为这些离群点是噪声点的时候)

②提升模型预测效果，学习这些离群点的规律

③用MAPE平均绝对百分误差来替代(当我们没有理由过滤掉这些噪声时。后文会介绍MAPE)

3.平均绝对误差 MAE (L1损失)

(Mean Absolute Error )

   预测值和真实值之差的绝对值求平均。

from sklearn.metrics import mean_absolute_error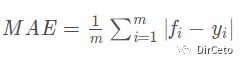

MAE越小越好，不常用是因为它不能求导！我们的优化目标往往是通过对损失函数求导来更新优化。

MAE对离群值没有那么敏感。但是对均值和标度很敏感。

4.平均绝对百分比误差 MAPE

(Mean Absolute Percentage Error )

#需要自己实现def mape(y_true, y_pred):    return np.mean(np.abs((y_pred - y_true) / y_true)) * 100

   MAPE就比MAE多了一个分母(除真实值)。

MAPE越小越好，MAPE为0%表示完美模型，大于100%为劣质模型。

缺点：同MAE不能求导，当真实值有数据等于0的时候，存在分母为0的情况，公式不可用！

5.R方值 R-squared(R2)

    【最好的衡量线性回归法的指标】

(Mean Squared Error )

from sklearn.metrics import r2_score

分类算法的衡量标准就是正确率百分比，在线性回归中也是有这样的衡量标准的——比较准确度。

直接理解：

    拟合一组数据，最简单模型作为baseline model ：就是取这组数据的均值并作直线(就相当于我们瞎猜的一个模型-均值模型)，已知这个简单模型的MSE大于线性回归的MSE，那大多少呢？

    我们将 线性回归的MSE/简单模型的MSE，用1减去这个分数 得到r2。

   分子：预测值和真实值的误差和的平方

    (我们的模型预测产生的错误)

   分母：均值和真实值的误差和的平方

    (基础模型预测产生的错误)

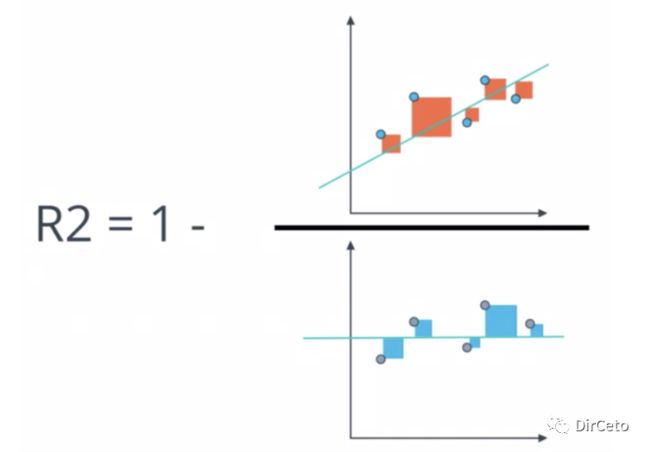
r2∈[-∞，1]，r2越趋向于1越好！

如果结果是0，说明我们的模型和瞎猜差不多

如果结果是1，说明我们的模型没错误

如果结果是－的，说明我们的模型还不如瞎猜(实际上也说明其实我们的数据毫无线性关系！)

一般认为超过0.8的模型拟合拟合度较高。

优势：是一个归一化的度量标准，既考虑了预测值和真值的差异，也考虑了问题本身真值间的差异。

二.二分类的常用指标

    分类有二分类和多分类。现实生活中大多数以二分类问题为主。

介绍指标之前的一些基本概念：

    阳性=真=正类=1

    阴性=假=负类=0

 当模型对这个样本预测的结果为1时候，可以认为这个模型对这个样本预测为真，或者正类，或者阳性。

二分类的常用指标有：

 准确率/精度(accuracy)

   精确率(查准率，precision_score,P)

   召回率(查全率，recall_score，R)

   F1分数

   PR曲线

   ROC-AUC

先回想一下混淆矩阵：

TP-正类预测为正类 √ 

TN-负类预测为负类 √

FP-负类预测为正类 ×

FN-正类预测为负类 ×

1.准确率 (Accuracy)

   被预测正确的比例。

    scoring = 'accuracy'

优点：简单，分对了就是分对了

缺点：准确度就是简单的计算出分对了的比例，没有对不同的类别进行区分，样本不均衡也不好使。

①存在重要差异性：当不同种类的分错的错误代价不同时候，如判断病危，将病危的人判断为非病危，损失极大。

②样本不均衡：如A类有995个，B类5个，我将1000个样本99.5%，你猜一个样本是不是A类的时候，99.5%的情况你都会猜对，岂不是成了大预言家？

这个标准不好!

2.精确率/精度/查准率 (Precision,P)

from sklearn.metrics import precision_score

   预测为正类的真的是正类的比例。

    我现在预测的所有为正类的，到底有多少是被正确分类？

分子：预测为正 真是为正

分母：预测为正 真实为正 + 预测为正 真实为负

    通俗来说：做一个谨慎的分类器，分类阈值较高

缺点：注重精确度的分类器会忽视除了正类以外的所有内容，没有什么意义。

必须搭配召回率一起评估价分类器！

3.召回率/查全率/真正类率(Recall，R)

   正类中被预测为正类的比例。

   我现在预测为正类的，占了所有正类的比例是多少？

分子：预测为正 真实为正

分母：预测为正 真实为正，预测为负 真实为正

   通俗来说：宁可错杀一千，不要放过一个 

from sklearn.metrics import recall_score

精确率和召回率必须一起来看：

 精准度和召回率是一对矛盾的量，一般情况下，准确率高召回率就低，召回率低准确率就高。鱼和熊掌不可兼得！

做搜索：就保证召回率的情况下提升准确率

做疾病监测，反垃圾：保证准确率的情况下提升召回率。

在对两者都高要求的情况下，引入了F1：

4.F1 分数(假设P和R同样重要)

   精确率和召回率的调和平均。

from sklearn.metrics import f1_score

只有当P和R都很高时候，该分类器才会得到较高的F1分数。

5.PR曲线(P横坐标，R纵坐标)

   直接绘制召回率和精度的来寻找P/R权衡的图。

    右上角面积越大说明越不好

代码：

6.受试者工作特性曲线 (ROC)

   真正类率(即召回率：正样本中被预测对的比例)

   假正类率FPR(负类被预测错的比例：就是负类被分错了，所以分子是真实负类被分为正类FP,分母是所有的真实负类：包括负类被正确的分为负类TN和负类被错误的分为正类FP【ps：这里会绕晕，想不通的别想了】)

召回率 越高，假正类率就越高，可以想象，召回率是宁可错杀不可放过，我找的越多，我分错的概率就越大！

ROC曲线：

横坐标：假正类率

纵坐标：真正类率

AUC：

ROC曲线下的面积，是一个概率值。

一个优秀的分类器应该离这条baseline越远越好

也就等于AUC面积越大越好

下图：虚线是一个纯随机分类器的ROC曲线

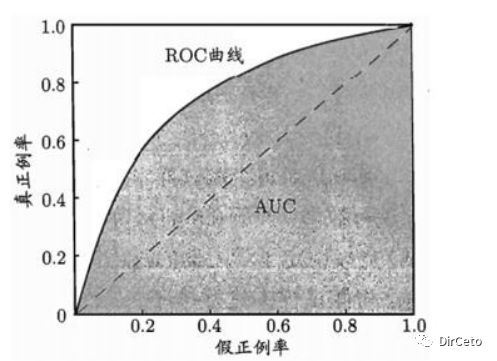
PR曲线和ROC曲线对比：

    与PR曲线相比，ROC曲线会更稳定，在正负类都足够的情况下，ROC曲线足够反映模型的评判能力。

但在正负类极其不均匀的情况下(如正类极少)，PR曲线能够更有效的反映整体分类情况。

①没有类不均衡：ROC

②正类超少/你更关注假正类(负类被预测为正类)：PR

③正类远大于负类：差别不大

三.多分类的常用指标

    前文中，介绍了二分类的几大常用指标：准确率accuracy，精确率precision，召回率recall等。对于多分类问题，通过sklearn包计算时候会有几种不同的算法。我们需要将计算P,R,f1的方法里的'average'参数修改为'micro'或'macro'或者'weighted'。

算法：

    micro

    macro

    weighted

样本不均衡时加入sample_weight参数

sklearn中计算precision_score：

from sklearn.metrics import precision_scoreprecision_score(y_true, y_pred, labels = None, pos_label =1 ,                  average='binary' , sample_weight = None)

其中 average 参数制定了该指标的计算方法

二分类时：默认'binary'

多分类时可选参数：'micro'，'macro'，’weighted'

我们假设现在是三分类，分别是 -1 ，0 ，1三类

情况：A.样本均衡——不加sample_weight

           B.样本不均衡——加sample_weight

     下面以precision_score算精度的方法为例,

       其他的评估指标precision, roc_auc_score, f1-score都是采用同样的方法。

---

A.不加sample_weight

1.micro

  micro指将所有的类的TP放在一起算precision

    就是把所有的类的TP(本身真正类分到正类)加和，再除以TP+FN(本身正类分到负类)，micro方法下的精度P和召回率R均等于准确率acc。

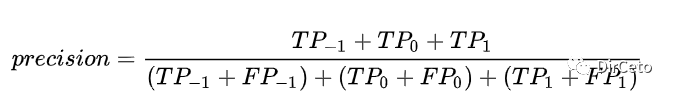
from sklearn.metrics import precision_scoreprecision_score(y_true, y_pred, average="micro")

2.macro

  macro指分别求出每个类的precision再算术平均。

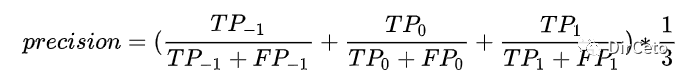
precision_score(y_true, y_pred, average="macro")

3.weighted

  macro是取算术平均，weighted是macro的改良版，macro是每个precision取均值，weighted是乘该类在总样本数的占比。

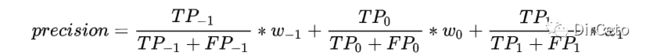
precision_score(y_true, y_pred, average="weighted")

B.加sample_weight

    当样本不均衡时，如0占80%，1和-1各占10%，每个类的数量差距很大，可以加入sample来调整样本。

0	240个
1	30个
-1	30个

1.先使用sklearn里的compute_sample_weight来计算sample_weight

sw = compute_sample_weight(class_weight = 'balance',y=y_true)

得到的sw是一个和y_true的shape相同的数据，每一个数代表该样本所在的sample_weight。

具体计算方法：总样本数/(类数*该类的个数)

    如-1的：300/(3*30)

2.将sw传入confusion_matrix中，得到一个新的混淆矩阵

cm = confusion_matrix(y_true, y_pred, sample_weight=sw)

一个新的混淆矩阵：

array([[33.33333333, 33.33333333, 33.33333333],
      [16.66666667, 66.66666667, 16.66666667],
      [16.66666667, 16.66666667, 66.66666667]])

使用该矩阵来得到TP,FN,FP。

---

上述为所有常用评价指标，谢谢阅读！