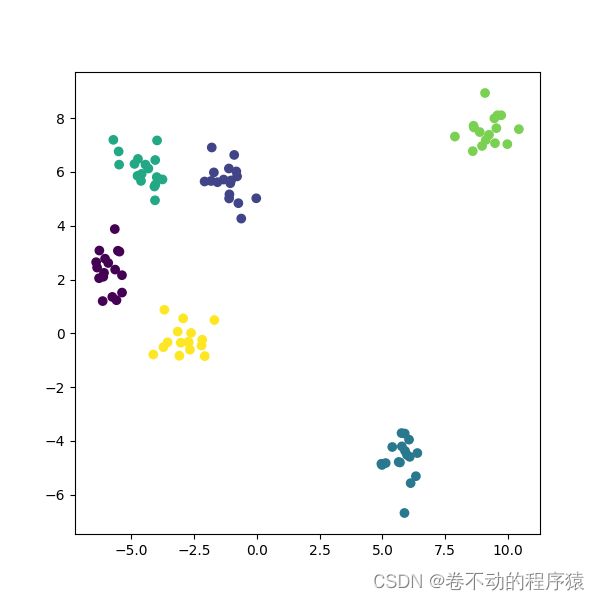
机器学习之K均值聚类算法K-Means（python代码实现）

K均值聚类（K-Means）

        k-means 算法：根据给定的数据样本构建 k 个划分聚类，每个划分聚类即为一个簇。

        该算法是一个典型的基于距离的聚类算法，采用距离作为相似性的评价指标（两个样本的距离越近，相似度就越大）。

每个数据样本必须属于而且只能属于一个簇。

同一簇中的数据样本相似度高，不同簇中的数据样本相似度较小。

聚类相似度是利用各簇中样本的均值来进行计算的。

注：因为在该算法第一步中是随机的选取任意k个对象作为初始聚类的中心，初始地代表一个簇，因此k个初始类聚类中心点的选取对聚类结果具有较大的影响。

聚类步骤：
1）随机指定k个质心点（中心点）
2）根据距离分类（靠近质心点的划归为同一类）
3）采用平均值更新质心点
4)重复迭代步骤2-3，直到质心点不在变化或者达到指点具体迭代次数。

python代码实现

import numpy as np
import matplotlib.pyplot as plt
# 引入scipy中的距离函数，默认欧式距离
from scipy.spatial.distance import cdist
# 从sklearn中直接生成聚类数据
from sklearn.datasets._samples_generator import make_blobs


# -------------1. 数据加载---------
x, y = make_blobs(n_samples=100, centers=6, random_state=1234, cluster_std=0.6)

#plt.figure(figsize=(6, 6))
#plt.scatter(x[:, 0], x[:, 1], c=y)
#plt.show()

# --------------2. 算法实现--------------
class K_Means(object):
    # 初始化，参数 n_clusters（K）、迭代次数max_iter、初始质心 centroids
    def __init__(self, n_clusters=5, max_iter=300, centroids=[]):
        self.n_clusters = n_clusters
        self.max_iter = max_iter
        self.centroids = np.array(centroids, dtype=np.float)

    # 训练模型方法，k-means聚类过程，传入原始数据
    def fit(self, data):
        # 假如没有指定初始质心，就随机选取data中的点作为初始质心
        if (self.centroids.shape == (0,)):
            # 从data中随机生成0到data行数的6个整数，作为索引值
            self.centroids = data[np.random.randint(0, data.shape[0], self.n_clusters), :]

        # 开始迭代
        for i in range(self.max_iter):
            # 1. 计算距离矩阵，得到的是一个100*6的矩阵
            distances = cdist(data, self.centroids)

            # 2. 对距离按有近到远排序，选取最近的质心点的类别，作为当前点的分类
            c_ind = np.argmin(distances, axis=1)

            # 3. 对每一类数据进行均值计算，更新质心点坐标
            for i in range(self.n_clusters):
                # 排除掉没有出现在c_ind里的类别
                if i in c_ind:
                    # 选出所有类别是i的点，取data里面坐标的均值，更新第i个质心
                    self.centroids[i] = np.mean(data[c_ind == i], axis=0)

    # 实现预测方法
    def predict(self, samples):
        # 跟上面一样，先计算距离矩阵，然后选取距离最近的那个质心的类别
        distances = cdist(samples, self.centroids)
        c_ind = np.argmin(distances, axis=1)

        return c_ind


dist = np.array([[121, 221, 32, 43],
                 [121, 1, 12, 23],
                 [65, 21, 2, 43],
                 [1, 221, 32, 43],
                 [21, 11, 22, 3], ])
c_ind = np.argmin(dist, axis=1)
print(c_ind)
x_new = x[0:5]
print(x_new)
print(c_ind == 2)
print(x_new[c_ind == 2])
np.mean(x_new[c_ind == 2], axis=0)

# --------------3. 测试------------
# 定义一个绘制子图函数
def plotKMeans(x, y, centroids, subplot, title):
    # 分配子图，121表示1行2列的子图中的第一个
    plt.subplot(subplot)
    plt.scatter(x[:, 0], x[:, 1], c='cyan')
    # 画出质心点
    plt.scatter(centroids[:, 0], centroids[:, 1], c=np.array(range(5)), s=100)
    plt.title(title)

kmeans = K_Means(max_iter=300, centroids=[[2, 1], [2, 2], [2, 3], [2, 4], [2, 5]])

plt.figure(figsize=(16, 6))
plotKMeans(x, y, kmeans.centroids, 121, 'start')

# 开始聚类
kmeans.fit(x)

plotKMeans(x, y, kmeans.centroids, 122, 'k-means')

# 预测新数据点的类别
x_new = np.array([[0, 0], [10, 7]])
y_pred = kmeans.predict(x_new)

print(kmeans.centroids)
print(y_pred)

plt.scatter(x_new[:, 0], x_new[:, 1], s=100, c='black')
plt.show()