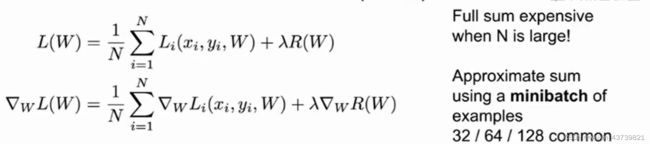深度学习-计算机视觉-基础学习笔记-01
图像分类的思想:收集大量已知图像数据并带有正确的标签,将以往通过一个函数传入一张图片并返回图片的类型的这个思想转变成,通过俩个函数,第一个函数传入大量的图片并通过该函数训练返回一个模型,该模型通过训练其内部参数不断得到优化。第二个函数传入训练好的模型和需要识别的图像并返回该图片的类型。
如何训练模型,大部分情况下我们无法得知哪组超参更合适,只能选择不断的调整参数来获得更好的模型。
那么该如何评估一组超参是好的呢?首先以下俩种情况不可取:
1、选择在训练的数据集上准确率最高的超参(只是获得了在该组数据集上表现良好的模型);
2、将数据集划分为训练集和测试集,选择在测试集上表现最好的超参(只是获得了在该组测试集上表现良好的模型)。
以上俩种情况都容易导致过拟合和较差的鲁棒性。
更好的方法应该是将数据集划分为训练集、验证集、测试集,在训练集上使用不同的超参来训练算法,在验证集上进行评估并选择一组表现最好的超参,然后将其在测试上验证效果,这才是你的算法在未见的新数据上的表现最好体现。
另外还有一种交叉验证的思想,其适合在小数据集中使用而在深度学习中并不常用,将训练集划分为很多份,然后选取不同的部分作为验证集,经过多轮训练与验证,这样可以对哪组超参表现更稳定具有更多的信心,但是在深度学习中当我们训练大型模型时训练非常消耗计算能力,所以该方法实际上并不实用。
线性分类器简介,其是参数模型中最简单的例子,比如我们向函数传入训练图像x和参数W,并得通过函数返回到各种标签的rank分,各个标签rank分的高低表明该图片是哪种标签的可能性较大。假设最简单的情况,x为代表将图像各个像素点拉伸成一个长的向量(比如一个32323的图片向量长度则为3072,乘三表示RGB三原色),f(x,W)=Wx+b,其中W为我们需要通过训练集不断训练得到的一个权重矩阵,b是偏好性设置参数,比如本身数据集中猫图片的占比比较多,那么我们可以将b向量中代表猫的部分适当增加。
而在这个情况中的W就是我们训练出来的线性分类器,该权重矩阵中每一个行向量可对应与数个类别相关的图片,告诉我们对应的像素对那个分类有多少影响,甚至可以将某一行向量取出来转换成图像,这样便可看到该类图片的模板是什么,比如下图中右上角对应汽车的模板。而这种类型划分可以将某种图片类型视为高维空间的某个点,然后点与点之间有分类面来划分一个类别,但是这种分类方式是有很大局限性的,现实中有很多情况是无法像下图示例那样线性可分的,可能在二维平面中没有办法通过绘制一条单独的直线来划分俩种类别。
所以当任何时候你有多模态数据,比如一个类别出现在不同的领域空间中,这是一个线性分类器可能有困境的地方。

损失函数和优化
损失函数
那么上面训练之后得到的权重矩阵该如何得到呢?我们可以用一个函数把W当做输入然后看一下得分,定量的估计W的好坏,这个函数称之为损失函数,比如常见的多分类SVM损失函数(计算见下图)。于是我们可以定量地衡量任何一个W是好是坏,然后找到一个有效的方式从W的可行域之中找到W的更好取值,这个过程便是优化。
损失函数优化的过程可以用上面图片分类的例子,比如f函数接受参数x图片和W权重矩阵,输出y即该图片识别后的分类标签或者各个标签的rank,总之y可以判别其预测的好不好,然后通过与真实的标签对比。最终的损失函数是在整个数据集中N个样本损失函数的平均值,定量地描述出参数W是否令人满意,然后在所有的W中找到在训练集上损失函数极小化的W。
通常刚开始训练时我们初始化W会使用一些很小的随机,所以训练初期各f返回的各个rank倾向于呈现较小的均匀分布的值。
所以比如我们使用多分类SVM损失函数并且图片拥有十个类,刚开始rank向量的所有数值都近乎为0,损失函数最终平均结果预计会是10-1=9 (过程比较复杂,可不看。大致过程是因为rank向量各个数值相等,所以数值间的差值没有达到我们设立的差值阈值比如是1(正确分值比不正确分值高出来的安全边距),而如果某次对应图片类别预测正确,即其rank对应正确图像类型的数值较高,相较其他所有类别图像的数值差值达到1以上,那么返回的此次损失函数值为0,而每次多分类SVM损失函数会计算该图片类型与其他所有类型的差值的和,所以初期最终结果是9),如果刚开始训练的时候第一次迭代使用这种分类SVM损失函数返回值并不等于类别-1,意味着你的程序可能有bug。
这是一个比较好的方法,当你使用各种各样的损失函数刚开始训练的时候你应该能够知道预期的损失是多少。
tips:如果将计算损失函数的max改为求max的平方效果会如何?
结果将完全不一样,因为损失函数就是告诉你的算法是什么类型的错误,改成平方后其会是非线性的方法,意味着改变了在好和坏之间的权衡,意味着一个非常不好的错误就会更加不好,成平方的不好。

上述分类SVM损失函数中求每个图像训练时的损失函数的python实现:
#x为图像像素向量,y为图像对应的正确的标签
def L_i_vectorized(x,y,w):
scores=W.dot(x)
margins=np.maximum(0,socres-scores[y]+1)
margins[y]=0
loss_i=np.sum(margins)
return loss_i
tips:如果有一个W,损失函数返回的值都是0,这个W唯一吗?
不唯一,比如2*W也是0,这里有一个问题,损失函数是告诉我们哪个W是我们想要的,那么如何从这些损失函数都是0的W之间做出选择呢?
其实基于上面的,我们只是在告诉分类器,我们需要找到可以拟合训练集的W,但其实我们并不关心其在训练集上的表现,我们只关心找到的分类器将其应用到测试数据,所以如果你只是告诉分类器只需要拟合训练集的话就容易导致过拟合。比如下图中经过蓝色点拟合出来的蓝色线,但是在测试集上我们真正想要的是绿色的直线。

所以为了解决上述问题,我们通常使用正则化的概念,鼓励模型选择更简单的W,其思想类似于奥卡姆剃刀,即要让一个理论的应用更广泛,选择更简约的假设。所以我们会在上述损失函数的基础上加上正则化惩罚项R,这样标准损失函数就有了数据丢失项和正则项。
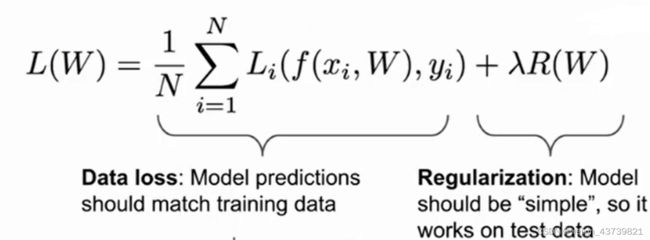
这里有一些超参λ用来平衡俩个项,让上图中的曲线成为绿色的直线,如果你想使用更复杂的模型,你需要克服这个惩罚(R(W)会返回较大数值),主要目的是为了减轻模型复杂度而不是去试图拟合数据。
不同种正在实践中使用的正则化如下,最常见的是L2正则化或权值衰减。L2正则化就是权重向量W的欧式范数或有时平方规范或者有时二次范数,理念是对W的欧式范数进行惩罚,用一种相对粗糙的方法去度量分类器的复杂性。有时也会看见L1正则化,比如其可以在这个W中鼓励稀疏。还有比如弹性网络正则化,是L1和L2的组合。还有最大规范正则化、脱网(dropout)或批量归一化 随机深度,这些概念这些年都比较火。在不同情况下L1、L2正则化可能会倾向完全相反的结果,所以具体问题具体分析,看你的模型的复杂度应该如何度量。
在下面的例子中,W1和W2与x相乘的结果都是1,但是如果使用L2正则化,就会倾向选择W2。
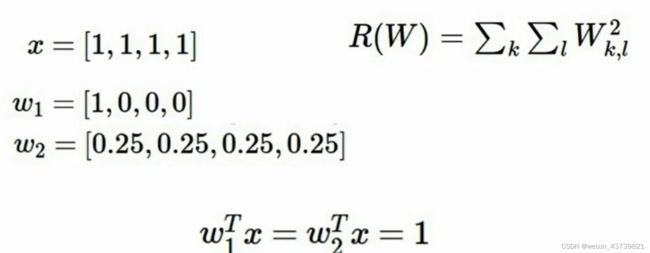
除了多类别SVM损失函数之外,另一个在深度学习中非常流行的选择是多项逻辑回归损失函数(多项逻辑斯蒂回归、多项式逻格斯回归)或者叫softmax loss(交叉熵损失),回想之前的函数F,给我们返回了十个数字,分别代表每个图片类型的得分,与SVM不同,在这里将会赋予这些得分一些额外的含义。并且会用其针对我们的图像类别去计算概率分布。
下图中Sk、Sj等就是Softmax function计算出的分数之一,我们将其指数化以便结果都是正数,接着用指数和来归一化得到概率分布,以此所有类别都得到相应概率,每个介于0到1且和为1。我们想要真实的标签的概率应当比较高并接近于1,然后我们损失函数返回值就是真实类别概率的对数再取负值(为什么取log,因为其单调,且观察图像可知真实标签概率越小,返回的数越大,找log函数最大值相对简单,这里情况就是真实标签概率无限接近1时返回值也无限接近0,返回最大值可以无穷大)


与SVM同理,训练初期各f返回的各个rank倾向于呈现较小的均匀分布的值,此时所有的S都很小近乎为0,那么返回的损失值应该是logc,c是类别总数,这里不在解释观察公式显然可知。所以如果在用这个softmax损失来训练一个模型那么第一次迭代的损失应该是logc,否则可能是代码出现了问题。
对比俩种损失函数,SVM它会得到这个数据点超过阈值要正确分类,然后不再关心那个数据点了(损失函数返回0),而softmax总是试图不断提高,每一个数据点都会越来越好,这是个有趣的差异,但实际中表现差异不会太大。
总结重述以上,我们有一些x(图片)和y(类别)的数据集,使用线性分类器(W)来获得一些分数函数(f),根据输入x来计算分数S,然后使用损失函数来定量计算我们的预测与y这个真实标签相比有多差,然后我们会经常给损失函数增加一个正则化的术语,试图选择更简单的模型。这是一个非常通用的描述很多我们称之为监督学习的东西。
问题是我们该如何做,如何才能真正发现这个W使损失最小化,下面就要讲到优化的主题。
优化
首先为了找到更好的W,一次次采用纯随机数并在损失函数中一次次尝试肯定是不行的,这是最差的算法。
不断优化W的过程相当于在山中中找到谷底的过程,山中可能没有路但是可以凭借感觉找到哪些路是向下的,然后在数学中就是需要找到多元函数的梯度,梯度代表着函数上升最快的方向,所以其负方向就是下降最快的方向,梯度向量上每个元素可以告诉我们每个方向上f的斜率。所以在深度学习中很多时候都是在计算函数的梯度,然后用这些梯度迭代来更新你的参数向量。
在计算机中计算梯度的一个简单方法是有限差分法:

在左边假设当前的W是这个向量参数,其损失值为1.25347,我们的目标是计算在损失值上的梯度dW,其是和W相同维数的向量,梯度中每个元素都会告诉我们在相关方向上移动一小步损失变化多少。计算有限差分只是将W的第一个元素累加一个很小的值h,然后用分类器重新计算rank和用损失函数重新计算损失值所有这些,可能因此损失函数降低到了1.25322,然后可以用这个有限差分在梯度的第一维实现有限差分逼近。然后重新将第一维的值恢复,如法炮制计算第二维…不断重复这样的过程。
虽然看起来很好,但其实这个方法也不尽人意,因为它实在是太慢了,如果卷积神经网络特别大,计算函数f会很慢,W也可能不像这里只有十个输入,可能是数以千万计,所以这个方法也不行。
幸运的是我们学过微积分,我们只需要写下损失的表达式使用微积分写下梯度的表达式,所以回到之前的方法,与迭代计算所有W维度有所不同,我们提前计算出梯度的表达式,然后从W值开始计算dW或每步的梯度,在实际中这种方法更好。
概括来说,现实中可能不会使用数值梯度,但它简单且有用处,实际上在计算梯度的时候我们总是使用解析梯度,但是数值梯度是有用的调试工具。现实中如何保证自己写入代码的解析表达式是正确的?可以使用数值梯度作为单元测试确保解析梯度的正确性,因为数值梯度计算起来时间过长所以需要减少问题的参数数量。

知道了如何计算梯度,好像只需三行简单的梯度下降算法代码,但是计算量巨大也是最为复杂的深度学习算法核心。在梯度下降算法中,首先我们初始化W为随机值,while true时我们计算损失和梯度,然后向梯度相反的方向更新W权重值,然后一直重复最后网格将会收敛。 步长(step_size)也被叫做学习率,是一个超参数,告诉我们每次计算梯度时在那个方向前进多少距离,步长过小,有可能会陷入局部最优解,它是你需要首先设定的最重要的一个超参数,在其他比如模型大小、需要多少正则化之前。
#Vanilla Gradient Descent
while True:
weights_grad=evaluate_gradient(loss_fun,data,weights)
weights+= - step_size * weights_grad #执行参数更新
基本的思想是如此,但也有许多不同的高级用法,利用每一步的梯度决定下一步的方向也有不同的更新策略,决定究竟如何使用这些梯度信息,这些会在后面继续介绍。
现在还有另一个问题,我们之前定义了损失函数,然后我们设定数据集的总误差是整个训练集也就是所有图片的误差的平均值,但实际中训练集N可能会非常大乃至百万级别,计算这些loss的成本非常大,要对f和损失函数进行百万次运算,要很长时间才能更新一次W。
所以实际中我们往往使用随机梯度下降,它不是整个训练集的误差和梯度值,而是在每一次迭代中选取一小部分训练样本成为minibatch(小批量),按惯例取2的n次幂如32/64/128等。然后用minibatch来估算误差总和以及实际梯度,可以把它看作对真实数值期望的一种蒙特卡洛估计,这就让我们的代码多了一行:
#Vanilla Minibatch Gradient Descent
while True:
data_batch=sample_training_data(data,256) #256批量
weights_grad=evaluate_gradient(loss_fun,data_batch,weights)
weights+= - step_size * weights_grad #执行参数更新
最后学习另一个概念,即图像特征。
此前我们将图片原始像素取出传入线性分类器里,但是因为多模态之类的原因,这样做的效果不会很好。所以当深度神经网络大规模运用之前常见做法是用俩步走策略。第一步计算图片的各种特征代表,比如计算与图片形象有关的数值,第二步将不同的特征向量合到一起得到图像的特征表述,将其传入线性分类器。
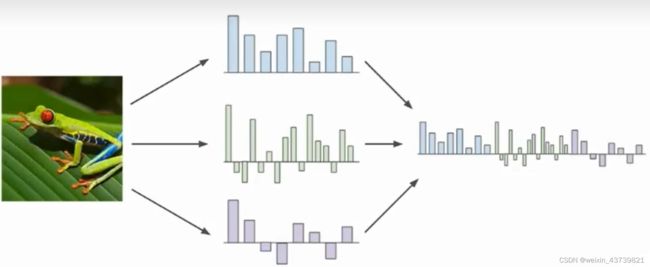
这么做的动机如下图所示,假设有一个左侧的训练集,有蓝红俩种类型,但是无法通过线性分类器划分一个线性决策边界,但是如果采用一个灵活的特征转换就可以,比如在这个例子中采用极坐标转换,就可以把复杂的数据集转成线性可分的。

所以问题就来到了需要找到正确的特征转换,从而计算出所关心问题的正确指标。对于图像来说将原始像素转换到极坐标不能起到什么作用,一些有可能起作用的图像特征表示比如颜色直方图、方向梯度直方图和词袋(从nlp中获得的灵感,从图像中采集图像块)等
反向传播和神经网络
反向传播
前面讲到W的解析梯度,那么如何计算任意复杂函数的解析梯度?当你使用神经网络时把所有参数的梯度公式写下来不现实,此时就需要用到一个叫做计算图的框架,用这类图来表示函数,图的结点表示计算的每一步,这样就能用所谓反向传播技术递归地调用链式法则来计算图中每个变量的梯度。
比如下面的例子,将每一步中间计算的结果也加上中间变量,从后往前计算梯度值,每一个节点都会得到从一个上游返回的梯度,计算到z节点我们就得到了最终损失关于z的梯度。
这样可以只是使用链式法则把非常复杂的表达式分解成一些计算结点从前往后计计算在特定输入下比如x和y对f的影响也就是梯度值而不用推导整个表达式。比如下面的q此时等于3、z等于-4而可以计算出q对f的影响是-4,从而可以计算出y对f的影响是-4。
TIPS:先向前传播才能反向传播,所以肯定是有具体值的,不是单纯只计算表达式。


更复杂的函数求梯度:
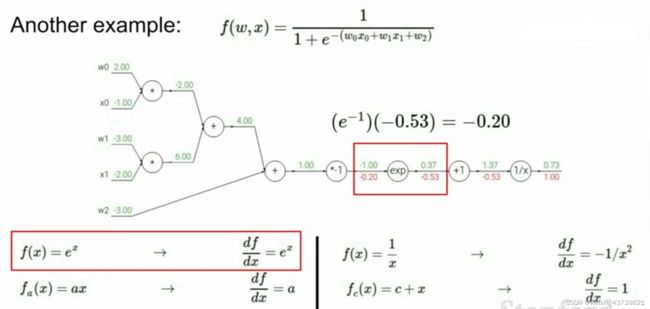
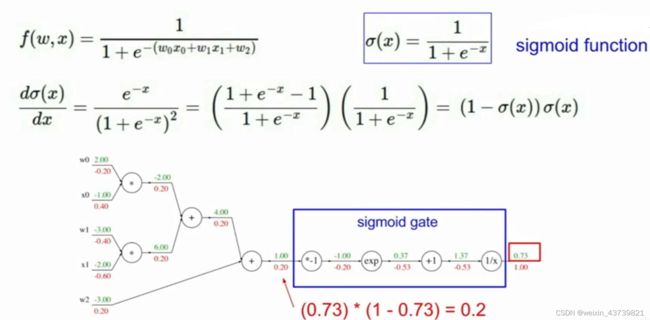
比如从+1结点传递给1/x结点的数值是1.37,然后1.37作为x传入f=1/x,那么求+1结点对1/x的影响,就要求1/x的导数,其为-1/x^2 .所以将1.37传入到 -1/x^2中可得-0.53,所以1/x结点对+1结点的梯度是-0.53,又1/x已经是最后一个结点,f对其的梯度是1,所以+1结点对f的影响就是1*(-0.53)
再比如*-1结点与exp结点,上游传递下来的梯度是-0.53,而本地梯度是exp函数求导的导函数带入*-1传给exp结点的数值,所以本地梯度是e的负一次方,所以f对*-1结点的梯度,也就是*-1结点对f的影响是-0.53*e^-1=-0.20,即用本地梯度乘以上游梯度即得这个参数对f的影响,以此类推。
所以相比推导对任意参数的梯度的解析表达式,这种方法简单在于所有我们处理过的本地梯度的表达式一旦被求好,我们只需要填充每个值就行,然后使用链式法则从后往前乘这些值,得到f对所有变量的梯度。
需要注意的是,在创建计算图的时候我们可以以我们想要的任意间隔尺寸来定义计算节点,在上图中我们把它分解为能达到的最简单的形式分解成加减乘除,实际上我们可以把一些结点结合在一起形成更复杂的结点,只要我们能写出那个节点的本地梯度。
实际运用中当变量是高维向量的情况整个计算流程还是一样的,唯一的区别在于我们刚才的梯度变成了雅克比矩阵,是一个包含了每个变量里可元素导数的矩阵,x、y----f---->z,就有z在每个x元素方向上的梯度。 其中雅克比矩阵每一行都是偏导数,矩阵的每个元素是输出向量的每个元素对输入向量每个元素分别求偏导的结果,所以下面图中结点的雅克比矩阵是4096*4096大小的。
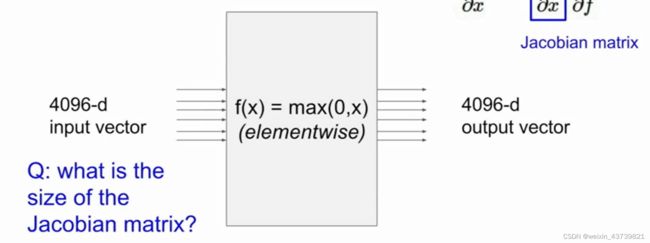
但是实际运算中多数情况下我们不需要计算这么大的雅克比矩阵,比如这里的max运算,输入的第一个元素只和输出的一个元素有联系,雅克比矩阵是一个对角矩阵,所以我们不需要写出整个矩阵,只需要求输出向量关于x的偏导然后把结果作为梯度填充进去即可。
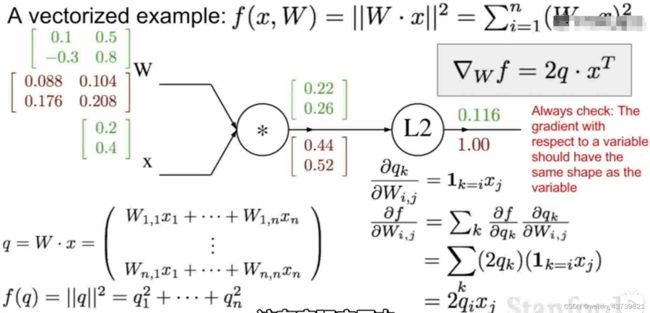
看一个向量的例子,f为W矩阵乘以x向量的平方,那么结点可看成中间结果f(q),最终结果是q向量中的平方和,q=Wx.首先假设特殊情况n=2,此时输入参数(绿色下标)如上,最终结果是0.116,从f(q)结点到f经历的是平方和,qi方求导可得2qi,所以f(q)结点对f影响是2q=[0.44,0.52]。
然后求f对W的梯度,Wx=q,q1对w1,i求导得x1,所以w1,1的梯度是x1*0.44=0.088,以此类推.最后推出的f关于W的梯度如右上角所示。
同时记住一个很重要的事情,检查变量梯度的向量大小,应该和变量大小一致,这是非常有用的完整性检查。
神经网络
一般来说神经网络就是由简单函数构成的一组函数,在顶层堆叠在一起,为了形成一个更复杂的非线性函数就用一种层次化的方式将它们堆叠起来,这便是最基本的多阶段分层计算。
举个例子在上面的十类图像分类中W的每行可看成一个图片的模板,然后车的模板看起来像是一个红色的车,那么现实中还会有其他颜色的车,可以将这些车也分成不同的模板,将max(0,W1x)作为第一层结果,然后由W2对第一次得分的中间值进行加权得到最终的得分,比如输入一个马的正脸,那么它在左侧马和右侧马的得分都是居中,但是它在最终的马的类别中的得分还是很高所以分类到马这一类。
所以也可以说神经网络就是一种计算图,它包含若干个线性层,而层与层之间通过非线性函数进行连接实现堆叠。
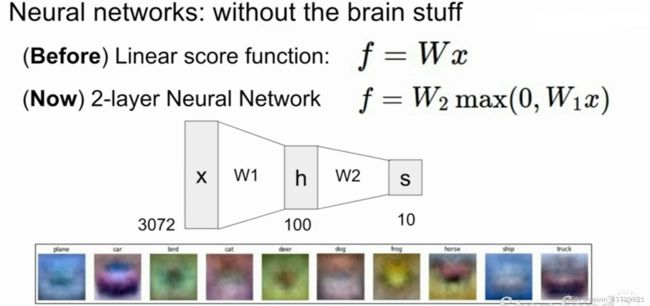
上面是俩层神经网络,之前我们叫的是俩层神经元网络,具体来讲有俩个线性层,针对每个线性层做了一次矩阵乘法,称之为俩个全连接层或单隐藏层神经网络,我们也可以堆更多层得到任意深度的神经网络,右边这个可以叫做三层神经网络或者叫双隐藏层神经网络

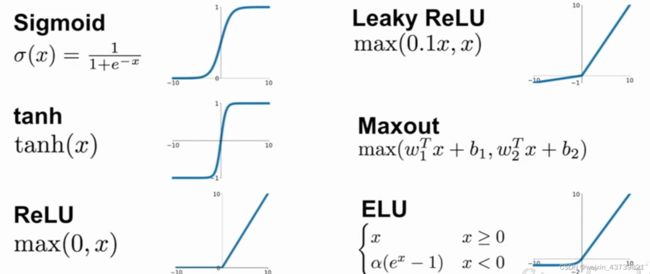
而这可以类比生物神经元之间的信号传递,脉冲信号传递在各个神经元之间很多神经元互相连接,每个神经元有多个树突接受给神经元的脉冲,然后细胞体集中处理这些传入的信号,接受整合再通过轴突将脉冲信号传向下游神经元。对每个计算节点方法也是类似的,计算图里的节点相互连接,我们需要输入或是信号x传入神经元所有x输入量比如x0、x1、x2等,采用比如赋予权重W的方法叠加汇合到一起得到一个激活函数,将激活函数应用在神经元的末端得到的值作为输出,最后将值传输到相关联的神经元。
而留意一下激活函数,它接受了所有输入输出一个值,如同上面的例子那个sigmoid激活函数一样,以及其他非线性函数可以类比神经元的触发,可以认为经过激活函数计算后的值是神经元传递的放电率。目前与生物神经元机制最相仿的非线性函数就是ReLU非线性函数,但是实际上的生物神经元远比这复杂的多的多。