数学建模学习笔记(八)——分类模型
文章目录
-
- 一、分类模型综述
- 二、逻辑回归
- 三、两点分布(伯努利分布)
- 四、连接函数的取法
- 五、Logistic回归模型
- 六、在SPSS中进行二元Logistic回归
- 七、预测结果较差的解决
- 八、Fisher线性判别分析
- 九、多分类问题
- 十、总结
一、分类模型综述
通过样本数据中的分类依据以及具体的分类类别,预测后续给出的对象属于哪一类,这就是分类模型。
本文将采用逻辑回归和Fisher线性判别分析这两种分类算法来进行对象分类。
二、逻辑回归
| 类型 | 模型 | Y的特点 | 例子 |
|---|---|---|---|
| 线性回归 | OLS、GLS(最小二乘) | 连续数值变量 | GDP、收入等 |
| 0 - 1回归 | logistic回归 | 二值变量(0 - 1) | 是否喜欢、是否到达等 |
| 定序回归 | prohibit定序回归 | 定序变量 | 等级评定,喜爱程度等 |
| 计数回归 | 泊松回归(泊松分布) | 计数变量 | 每分钟车流量,次数等 |
| 生存回归 | Cox等比例风险回归 | 生存变量 | 企业、产品的寿命等 |
逻辑回归的因变量即为二值变量类型,可以将 y y y 看作属于某一类的概率—— y ⩾ 0.05 y \geqslant 0.05 y⩾0.05,则属于这一类;反之, y ⩽ 0.05 y \leqslant 0.05 y⩽0.05,则不属于这一类。
三、两点分布(伯努利分布)
| 事件 | 1 | 0 |
|---|---|---|
| 概率 | p p p | 1 − p 1 - p 1−p |
在给定 x \mathbf{x} x 的情况下,考虑 y y y 的两点分布概率
{ P ( y = 1 ∣ x ) = F ( x , β ) P ( y = 0 ∣ x ) = 1 − F ( x , β ) \left\{ \begin{aligned} &P(y = 1|\mathbf{x}) = F(\mathbf{x}, \mathbf{\beta}) \\ &P(y = 0|\mathbf{x}) = 1 - F(\mathbf{x}, \mathbf{\beta}) \end{aligned} \right. {P(y=1∣x)=F(x,β)P(y=0∣x)=1−F(x,β) 注:一般 F ( x , β ) = F ( x i ′ β ) F(\mathbf{x}, \mathbf{\beta}) = F(\mathbf{x_i'\beta}) F(x,β)=F(xi′β)
F ( x , β ) F(\mathbf{x}, \beta) F(x,β) 称为连接函数,它将解释变量 x x x 和被解释变量 y y y 连接起来。
我们只需要保证 F ( x , β ) F(\mathbf{x}, \beta) F(x,β) 是值域在 [ 0 , 1 ] [0, 1] [0,1] 上的函数,就能保证 0 ⩽ y ^ ⩽ 1 0 \leqslant \hat{y} \leqslant 1 0⩽y^⩽1。
根据两点分布求概率的公式: E ( y ∣ x ) = 1 × P ( y = 1 ∣ x ) + 0 × P ( y = 0 ∣ x ) = P ( y = 1 ∣ x ) E(y|\mathbf{x}) = 1 \times P(y = 1|\mathbf{x}) + 0 \times P(y = 0|\mathbf{x}) = P(y = 1|\mathbf{x}) E(y∣x)=1×P(y=1∣x)+0×P(y=0∣x)=P(y=1∣x),因此可以将 y ^ \hat{y} y^ 理解为 y = 1 y = 1 y=1 发生的概率。
四、连接函数的取法
- F ( x , β ) F(\mathbf{x}, \beta) F(x,β) 可以取为标准正态分布的累积密度函数( c d f cdf cdf): F ( x , β ) = Φ ( x i ′ β ) = ∫ − ∞ x i ′ β 1 2 π e − t 2 2 d t F(\mathbf{x}, \beta) = \Phi(\mathbf{x_i}'\beta) = \int^{\mathbf{x_i}'\beta}_{-\infty}\frac{1}{\sqrt{2\pi}}e^{-\frac{t^2}{2}}dt F(x,β)=Φ(xi′β)=∫−∞xi′β2π1e−2t2dt(probit回归)
- F ( x , β ) F(\mathbf{x}, \beta) F(x,β) 可以取为 S i g m o i d Sigmoid Sigmoid 函数 F ( x , β ) = S ( x i ′ β ) = e x p ( x i ′ β ) 1 + e x p ( x i ′ β ) F(\mathbf{x}, \beta) = S(\mathbf{x_i}'\beta) = \frac{exp(\mathbf{x_i}'\beta)}{1 + exp(\mathbf{x_i}'\beta)} F(x,β)=S(xi′β)=1+exp(xi′β)exp(xi′β)(logistic回归)
可以看出,前者计算积分会比较困难,因此我们可以选择使用更为方便的logistic模型。
五、Logistic回归模型
在给定 x \mathbf{x} x 的情况下,考虑 y y y 的两点分布概率 { P ( y = 1 ∣ x ) = F ( x , β ) P ( y = 0 ∣ x ) = 1 − F ( x , β ) \left\{ \begin{aligned} &P(y = 1|\mathbf{x}) = F(\mathbf{x}, \beta) \\ &P(y = 0|\mathbf{x}) = 1 - F(\mathbf{x}, \beta) \end{aligned} \right. {P(y=1∣x)=F(x,β)P(y=0∣x)=1−F(x,β)因为 E ( y ∣ x ) = 1 × P ( y = 1 ∣ x ) + 0 × P ( y = 0 ∣ x ) = P ( y = 1 ∣ x ) E(y|\mathbf{x}) = 1 \times P(y = 1|\mathbf{x}) + 0 \times P(y = 0|\mathbf{x}) = P(y = 1|\mathbf{x}) E(y∣x)=1×P(y=1∣x)+0×P(y=0∣x)=P(y=1∣x),因此可以将 y ^ \hat{y} y^ 理解为 y = 1 y = 1 y=1 发生的概率。
y i ^ = P ( y i = 1 ∣ x ) = S ( x i ′ β ) = e x p ( x i ′ β ) 1 + e x p ( x i ′ β ) = e β 0 ^ + β 1 ^ x 1 i + β 2 ^ x 2 i + ⋯ + β k ^ x k i 1 + e β 0 ^ + β 1 ^ x 1 i + β 2 ^ x 2 i + ⋯ + β k ^ x k i \hat{y_i} = P(y_i = 1|\mathbf{x}) = S(\mathbf{x_i}'\beta) = \frac{exp(\mathbf{x_i}'\beta)}{1 + exp(\mathbf{x_i}'\beta)} \\= \frac{e^{\hat{\beta_0} + \hat{\beta_1}x_{1i} + \hat{\beta_2}x_{2i} + \cdots + \hat{\beta_k}x_{ki}}}{1 + e^{\hat{\beta_0} + \hat{\beta_1}x_{1i} + \hat{\beta_2}x_{2i} + \cdots + \hat{\beta_k}x_{ki}}} yi^=P(yi=1∣x)=S(xi′β)=1+exp(xi′β)exp(xi′β)=1+eβ0^+β1^x1i+β2^x2i+⋯+βk^xkieβ0^+β1^x1i+β2^x2i+⋯+βk^xki 如果 y i ^ ⩾ 0.5 \hat{y_i} \geqslant 0.5 yi^⩾0.5,则认为其预测的 y = 1 y = 1 y=1;否则则认为其预测的 y = 0 y = 0 y=0
六、在SPSS中进行二元Logistic回归
回归结果:

回归结果表示19个苹果样本,预测为苹果的有14个,正确率为73.7%;同理,预测为橙子的结果有15个,预测的正确率为78.9%。

通过这样的回归我们便可以知道 β 0 , β 1 , ⋯ , β k \beta_0, \beta_1, \cdots, \beta_k β0,β1,⋯,βk 的值(表格第三列)。
将后续数据带入方程后,若 y i ^ ⩾ 0.5 \hat{y_i} \geqslant 0.5 yi^⩾0.5,则说明其预测的结果是苹果,否则则为橙子。
同时,我们还可以在表格中看到这两列:

这里可以查看具体预测的值和具体的预测结果。
七、预测结果较差的解决
若对预测结果不满意,可以在logistic回归模型中加入平方项、交互项等
如果加入了平方项,那么预测的结果:
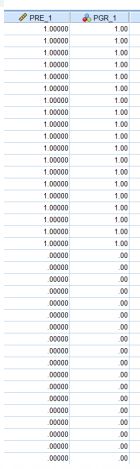
完全符合,这种现象叫做过拟合现象。其对于样本数据预测得非常好,但是对于样本外的数据得预测效果可能会差很多。
那么我们该如何确定合适得预测模型呢?
可以将数据分为训练组和测试组(一般是八二开),让训练组取估计模型,然后用测试组得数据来进行测试。可以多进行几次,求得每个模型的平均准确率,取准确率最高的那个模型。(交叉验证)
八、Fisher线性判别分析
- 主要思想
给定训练集样例,设法将样例投影到一维的直线上,使得同类样例的投影点尽可能接近和密集,异类投影点尽可能远离。 - 在SPSS中进行Fisher线性判别分析
结果为:
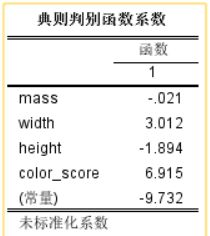
这个表格表示线性系数。
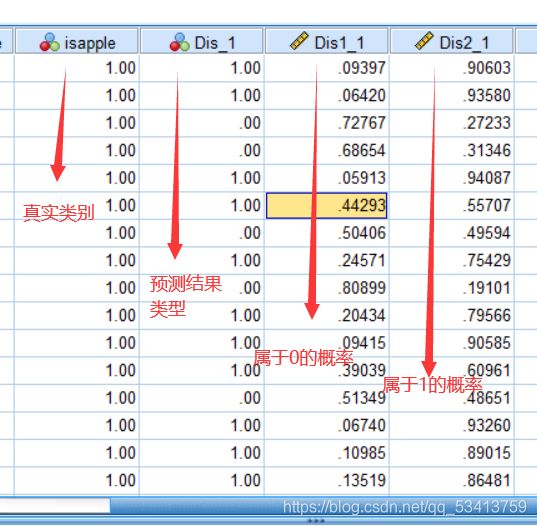
还可以从表格后面多出的列中得到具体的预测结果。
九、多分类问题
- 多分类问题
在二分类的问题上,类别不再是只有两个类别,现在有多个类别。 - 使用Logistic回归解决多分类问题
在SPSS中进行logistic回归分析,可以得出结果:

可以得出预测分类结果。 - 使用Fisher判别分析解决多分类问题
同样可以使用Fisher判别分析来求解多分类问题。在定义范围的时候将范围扩大即可。
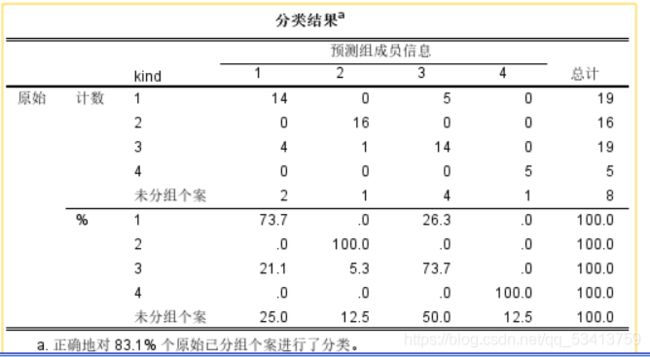
从结果表格中同样可以得出预测分类结果。
十、总结
解决分类模型,主要步骤可以总结为一下几点:
- 确定类别以及分类数据;
- Logistic回归 or Fisher判别分析?
- 若是Logistic回归,预测结果怎么样?是否需要训练出合适的模型?
- 根据模型在SPSS中调用对应的命令得出结果;
- 对结果进行解释。