OpenCV图像处理专栏十七 | 清华大学《基于单幅图像的快速去雾》C++复现（有一定工程意义）

代码开源在 https://github.com/BBuf/Image-processing-algorithm，感兴趣给我来个星星呗。

1. 前言

这是OpenCV图像处理算法朴素实现专栏的第17篇文章。今天为大家带来一篇之前看到的用于单幅图像去雾的算法，作者来自清华大学，论文原文见附录。

2. 雾天退化模型

之前在介绍何凯明博士的暗通道去雾论文OpenCV图像处理专栏六 | 来自何凯明博士的暗通道去雾算法(CVPR 2009最佳论文)的时候已经讲到了这个雾天退化模型，我们这里再来回顾一下。在计算机视觉领域，通常使用雾天图像退化模型来描述雾霾等恶劣天气条件对图像造成的影响，该模型是McCartney首先提出。该模型包括衰减模型和环境光模型两部分。模型表达式为：

$I(x)=J(x)e^{-rd(x)}+A(1-e^{-rd(x)})...........................(1)$

其中，$x$是图像像素的空间坐标，$H$是观察到的有雾图像，$F$是待恢复的无雾图像，$r$表示大气散射系数，$d$代表景物深度，$A$是全局大气光，通常情况下假设为全局常量，与空间坐标$x$无关。

公式(1)中的$e^{-r(dx)}$表示坐标空间$x$处的透射率，我们使用$t(x)$来表示透射率，于是得到公式（2）：

$I(x)=J(x)t(x)+A(1-t(x)).............................(2)$

由此可见，图像去雾过程就是根据$I(x)$求解$J(x)$的过程。要求解出$J(x)$，还需要根据$I(x)$求解出透射率$t(x)$和全局大气光$A$。实际上，所有基于雾天退化模型的去雾算法就是是根据已知的有雾图像$I(x)$求解出透射率$t(x)$和全局大气光$A$。

对于暗通道去雾算法来说，先从暗原色通道中选取最亮的0.1%比例的像素点，然后选取原输入图像中这些像素具有的最大灰度值作为全局大气光值$A$。RGB三通道中每一个通道都有一个大气光值。

然后根据公式(2)可以得出：

$t(x)=\frac{A-I(x)}{A-J(x)}...........................(3)$

首先可以确定的是$t(x)$的范围是$[0,1]$，$I(x)$的范围是$[0,255]$，$J(x)$的范围是$[0,255]$。$A$和$I(x)$是已知的，可以根据$J(x)$的范围从而确定$t(x)$的范围。已知的条件有：

$0<=J(x)<=255,0<=I(x)<=A,0<=J(x)<=A,0<=t(x)<=1...............(4)$

$=>t(x)>=\frac{A-I(x)}{A-0}=\frac{A-I(x)}{A}=1-\frac{I(x)}{A}..................(5)$

根据(4)和(5)推出：
$1-\frac{I(x)}{A}<=t(x)<=1..................................(6)$

因此初略估计透射率的计算公式：

$t(x)=1-\frac{I(x)}{A}...........................................(7)$

最后为了保证图片的自然性，增加一个参数$w$来调整透射率 ：

$t(x)=1-w\frac{I(x)}{A}..............................(8)$

好了，上面复习完了何凯明博士的暗通道去雾，我们一起来看看清华大学这篇论文。

3. 算法流程

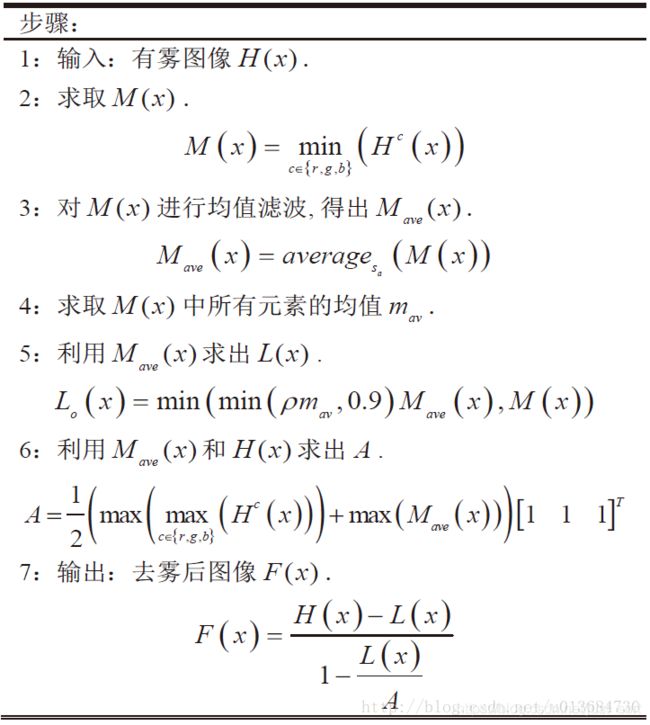
实际上有了这个算法流程就可以写出代码了，不过为了加深理解可以看下面的一些推导。

4. 一些推导

我们知道去雾的步骤主要就是估计全局大气光值$A$和透射率$t(x)$，因此，本文就是根据输入图像估计$A$和$L(x)$（这篇论文使用了$L(x)$来代替$A(1-t(x))$），然后根据雾天退化模型求取去雾后的图像。

4.1 估计透射率t(x)

从第二节的介绍我们知道

$t(x)>=1-\frac{H(x)}{A}...............................(2)$

然后这篇论文使用了$L(x)$来代替$A(1-t(x))$，即：

$L(x)=A(1-t(x)).............................(1)$。

我们取$H(x)$三个通道的最小值并记为：

$M(x)=mi{n}_{c\in r,g,b}(H^c(x)).......................(3)$

所以公式2变换为

$t(x)>=1-\frac{M(x)}{A}...................................(4)$

对公式(4)右边进行均值滤波：

$meadia{n}_{s_a}(1-\frac{M(x)}{A})=1-\frac{media{n}_{s_a}(M(x))}{A}=1-\frac{{\sum }_{y\in \Omega (x)M(y)}}{A{s}_a^2}...........(5)$

其中$s_a$代表均值滤波的窗口大小，$\Omega (x)$表示像素$x$的$s_a\times s_a$的邻域。

均值滤波后的结果可以反映$t(x)$的大致趋势，但与真实的$t(x)$还差一定的绝对值，因此，我们先得出透射率的粗略估计值：

$t(x)=1-\frac{M_{ave}(x)}{A}+\phi \frac{M_{ave}(x)}{A}=1-\delta \frac{M_{ave}(x)}{A}................(6)$

其中$M_{ave}(x)=media{n}_{s_a}(M(x)),\delta =1-\phi ,\phi \in [0,1]$，因此$\delta \in [0,1]$。

为了防止去雾后图像出现整体画面偏暗，这里根据图像的均值来调整$\delta$，即：

$\delta =\rho m_{ave}$

其中$m_{ave}$是$M(x)$中所有元素的均值，$\rho$是调节因子。

因此可以得到透射率的计算公式:

$t(x)=max(1-min(\rho m_{av},0.9)\frac{M_{ave}(x)}{A},1-\frac{M(x)}{A})...................(7)$

结合公式(1)推出：

$L(x)=min(min(\rho m_{av},0.9)M_{ave}(x),M(x))..........(8)$。

4.2 估计全球大气光值

公式(5)中第一个等式左侧的表达式取值范围为$[0,1]$，由此得出

$A>=max(M_{ave}(x))$

一般情况下又存在

$A<=max(ma{x}_{c\in r,g,b(H^c(x))})$

(KaiMing He的暗通道先验理论)。这样就初步确定了全局大气光的范围，为了能快速获取全局大气光，文章直接取两者的平均值作为全局大气光值，即：

$A=1/2(max(H(x))+max(M_{ave}(x)))$…(9)。

然后大气光值$A$和$L(x)$都搞定了，那么带入算法流程中的最后一个公式就可以获取最后的图像了。

5. 代码实现

下面是代码实现。

#include 
#include 
#include 
#include 
using namespace cv;
using namespace std;

int getMax(Mat src) {
	int row = src.rows;
	int col = src.cols;
	int temp = 0;
	for (int i = 0; i < row; i++) {
		for (int j = 0; j < col; j++) {
			temp = max((int)src.at(i, j), temp);
		}
		if (temp == 255) return temp;
	}
	return temp;
}

Mat dehaze(Mat src) {
	double eps;
	int row = src.rows;
	int col = src.cols;
	Mat M = Mat::zeros(row, col, CV_8UC1);
	Mat M_max = Mat::zeros(row, col, CV_8UC1);
	Mat M_ave = Mat::zeros(row, col, CV_8UC1);
	Mat L = Mat::zeros(row, col, CV_8UC1);
	Mat dst = Mat::zeros(row, col, CV_8UC3);
	double m_av, A;
	//get M
	double sum = 0;
	for (int i = 0; i < row; i++) {
		for (int j = 0; j < col; j++) {
			uchar r, g, b, temp1, temp2;
			b = src.at(i, j)[0];
			g = src.at(i, j)[1];
			r = src.at(i, j)[2];
			temp1 = min(min(r, g), b);
			temp2 = max(max(r, g), b);
			M.at(i, j) = temp1;
			M_max.at(i, j) = temp2;
			sum += temp1;
		}
	}
	m_av = sum / (row * col * 255);
	eps = 0.85 / m_av;
	boxFilter(M, M_ave, CV_8UC1, Size(51, 51));
	double delta = min(0.9, eps*m_av);
	for (int i = 0; i < row; i++) {
		for (int j = 0; j < col; j++) {
			L.at(i, j) = min((int)(delta * M_ave.at(i, j)), (int)M.at(i, j));
		}
	}
	A = (getMax(M_max) + getMax(M_ave)) * 0.5;
	for (int i = 0; i < row; i++) {
		for (int j = 0; j < col; j++) {
			int temp = L.at(i, j);
			for (int k = 0; k < 3; k++) {
				int val = A * (src.at(i, j)[k] - temp) / (A - temp);
				if (val > 255) val = 255;
				if (val < 0) val = 0;
				dst.at(i, j)[k] = val;
			}
		}
	}
	return dst;
}

int main() {
	Mat src = imread("F:\\fog\\1.jpg");
	Mat dst = dehaze(src);
	cv::imshow("origin", src);
	cv::imshow("result", dst);
	cv::imwrite("F:\\fog\\res.jpg", dst);
	waitKey(0);
	return 0;
}

6. 结果

7. 结论

算法里面有2个参数可以自己调节，滤波的半径和$\rho$。具体如何调节？我就不放在这里说了，这个算法后面会在我的新专题里面进行一遍优化，到时候再来回答这个问题。如果你迫切需要这个算法的实现或者对它感兴趣，可以自己尝试调整这两个参数获得想要的效果。这里的均值滤波也可以换成我们之前讲的Side Window Filter说不定可以获得更好的效果。

8. 参考

• https://blog.csdn.net/u013684730/article/details/76640321
• https://www.cnblogs.com/Imageshop/p/3410279.html

---

欢迎关注GiantPandaCV, 在这里你将看到独家的深度学习分享，坚持原创，每天分享我们学习到的新鲜知识。( • ̀ω•́ )✧

有对文章相关的问题，或者想要加入交流群，欢迎添加BBuf微信：