深度学习模型压缩与加速

前言

压缩与加速对于深度学习模型的端侧部署至关重要，但假设你的模型部署在服务端，模型的压缩与加速显得作用并不是特别大。在前一篇博客中，深度学习 模型压缩之知识蒸馏介绍了蒸馏的知识。我对知识蒸馏个人看法是没太大的必要去设计这样的网络训练，因为知识蒸馏需要花费功夫去训练一个好的教师模型，然后通过这个教师模型去训练学生模型（轻量模型），在这个过程中，也可以对教师模型进行压缩与量化从而达到模型的轻量化。另一方面，除非你的模型部署在端侧，否则一个大型的模型部署在服务器上不需要深度考虑模型的压缩与量化。

接下来本博客介绍一些模型压缩与加速的方法，包括两个方面：1. 设计网络结构实现加速；2. 对模型进行剪枝与量化。

模型Slimming

模型复杂度

在模型压缩之前需要弄清楚模型一些指标参数，其中包括：

• model size
• Runtime Memory
• Number of computingf operations

model size

模型的大小一般用参数量来衡量，参数量的单位是个，多少个训练参数。但是由于很多模型参数量太大，一般用兆（M）来衡量。然而模型在实际计算中除了包含参数量，还包括网络架构信息和优化器的信息（graph）等。比如存储一个一般的CNN模型(ImageNet训练)需要大于300MB。

Run time Memory

模型运行时所占的内存，该指标主要针对端侧硬件能力极为有限的设备

Number of computing operations

该参数为模型的计算量。

1. FLOPs。
   只需在parameters的基础上再乘以feature map的大小即可，即对于某个卷积层，它的FLOPs数量为：$$FLOPS{|}_{bias}=2K_{in}\times K_{out}\times C_{in}\times C_{out}\times H_{out}\times W_{out}$$$$FLOPS{|}_{nobias}=(2K_{in}\times K_{out}\times C_{in}-1)\times C_{out}\times H_{out}\times W_{out}$$对于全连接层，由于不存在权值共享，它的FLOPs数目即是该层参数数目：$$FLOPs=(2N_{in}-1)N_{out}$$ $N_{in}{N}_{out}$为乘法的运算量，$(N_{in}-1)N_{out}$为加法的运算量。
2. MACs
   设有全连接层为：

y = w[0]*x[0]+w[1]*x[1]+w[2]*x[2]+...+w[8]*x[8]

对于上式而言共有9次乘加，即9MACs（实际上，9次相乘、9-1次相加，但为了方便统计，将计算量近似记为9MACs。所以近似来看 $1MACs\approx 2FLOPs$。(需要指出的是，现有很多硬件都将乘加运算作为一个单独的指令)。
全连接层MACs的计算：$$MACC=N_{in}\times N_{out}$$激活层MACs的计算：激活层不计算MAC，计算FLOPs。假设激活函数为$$y=max(x,0)$$则计算量为$N_{out}FLOPs$，不同的激活函数有不同的计算方式，具体问题具体分析。

模型压缩

在模型压缩领域，有一些常用的方法，比如：剪枝，量化，蒸馏，轻量化模块设计，低秩分解，加法网络等等。

1. 剪枝就是通过去除网络中冗余的channels，filters，neurons，or layers以得到一个更轻量级的网络，同时不影响性能。 代表性的工作有：

奇异值分解SVD(NIPS 2014)： Exploiting linear structure within convolutional networks for efficient evaluation
韩松(ICLR 2016)： Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding
(NIPS 2015)： Learning both weights and connections for efficient neural network
频域压缩(NIPS 2016)： Packing convolutional neural networks in the frequency domain
Filter Reconstruction Error(ICCV 2017)： Thinet: A filter level pruning method for deep neural network compression
LASSO regression(ICCV 2017)： Channel pruning for accelerating very deep neural networks
Discriminative channels(NIPS 2018)： Discrimination-aware channel pruning for deep neural networks
剪枝(ICCV 2017)： Channel pruning for accelerating very deep neural networks
neuron level sparsity(ECCV 2017)： Less is more: Towards compact cnns
Structured Sparsity Learning(NIPS 2016)： Learning structured sparsity in deep neural networks

2. 轻量化模块设计就是设计一些计算效率高，适合在端侧设备上部署的模块。 代表性的工作有：

Bottleneck(ICLR 2017)： Squeezenet: Alexnet-level accuracy with 50x fewer parameters and 0.5 mb model size
MobileNet(CVPR 2017)： Mobilenets: Efficient convolutional neural networks for mobile vision applications
ShuffleNet(CVPR 2018)： Shufflenet: An extremely efficient convolutional neural network for mobile devices
SE模块(CVPR 2018)： Squeeze-and-excitation networks
无参数的Shift操作(CVPR 2018)： Shift: A zero flop, zero parameter alternative to spatial convolutions
Shift操作填坑(Arxiv)： Shift-based primitives for efficientconvolutional neural networks
多用卷积核(NIPS 2018)： Learning versatile filters for efficient convolutional neural networks
GhostNet(CVPR 2020)： GhostNet: More features from cheap operations

3. 蒸馏就是过模仿教师网络生成的软标签将知识从大的，预训练过的教师模型转移到轻量级的学生模型。 代表性的工作有：

Hinton(NIPS 2015)： Distilling the knowledge in a neural network
中间层的特征作为提示(ICLR 2015)： Fitnets: Hints for thin deep nets
多个Teacher(SIGKDD 2017)： Learning from multiple teacher networks
两个特征得新知识再transfer(CVPR 2017)： A gift from knowledge distillation: Fast optimization, network minimization and transfer learning

4. 量化就是减少权重等的表示的位数，比如原来网络权值用32 bit存储，现在我只用8 bit来存储，以减少模型的Memory为原来的$\frac{1}{4}$；更有甚者使用二值神经网络。 代表性的工作有：

量化：
(ICML 2015)： Compressing neural networks with the hashing trick
(NIPS 2015)： Learning both weights and connections for efficient neural network
(CVPR 2018)： Quantization and training of neural networks for efficient integer-arithmetic-only inference
(CVPR 2016)： Quantized convolutional neural networks for mobile devices
(ICML 2018)： Deep k-means: Re-training and parameter sharing with harder cluster assignments for compressing deep convolutions
(CVPR 2019)： Learning to quantize deep networks by optimizing quantization intervals with task loss
(CVPR 2019)： HAQ: Hardware-Aware automated quantization with mixed precision.
二值神经网络：
Binarized weights(NIPS 2015)： BinaryConnect: Training deep neural networks with binary weights during propagations
Binarized activations(NIPS 2016)： Binarized neural networks
XNOR(ECCV 2016)： Xnor-net: Imagenet classification using binary convolutional neural networks
more weight and activation(NIPS 2017)： Towards accurate binary convolutional neural network
(ECCV 2020)： Learning Architectures for Binary Networks
(ECCV 2020)： BATS: Binary ArchitecTure Search

5. 低秩分解就是将原来大的权重矩阵分解成多个小的矩阵，而小矩阵的计算量都比原来大矩阵的计算量要小。 代表性的工作有：

低秩分解(ICCV 2017)： On compressing deep models by low rank and sparse decomposition
乐高网络(ICML 2019)： Legonet: Efficient convolutional neural networks with lego filters
奇异值分解(NIPS 2014)： Exploiting Linear Structure Within Convolutional Networks for Efficient Evaluation

6. 加法网络就是：利用卷积所计算的互相关性其实就是一种“相似性的度量方法”，所以在神经网络中用加法代替乘法，在减少运算量的同时获得相同的性能。 代表性的工作有：

(CVPR 20)： AdderNet: Do We Really Need Multiplications in Deep Learning?
(NIPS 20)： Kernel Based Progressive Distillation for Adder Neural Networks
(Arxiv)： AdderSR: Towards Energy Efficient Image Super-Resolution

7. Slimming

(ICCV 2017)：清华张长水，黄高团队： Learning Efficient Convolutional Networks through Network Slimming
(ECCV 2020)：得克萨斯大学奥斯汀分校团队： GAN Slimming: All-in-One GAN Compression by A Unified Optimization Framework

加速网络的设计

分组卷积

分组卷积即将输入的feature maps分成不同的组（沿channel维度进行分组），然后对不同的组分别进行卷积操作，即每一个卷积核置于输入的feature maps的其中一组进行连接，而普通卷积操作则是与所有的feature maps进行连接计算。分组数k越多，卷积操作的总参数量和总计算量就越少。然而分组卷积有一个致命的缺点就是不同分组的通道间减少了信息流通，即输出的feature maps只考虑了输入特征的部分信息，因此在实际应用的时候会在分组卷积之后进行信息融合操作。

1. shuffle net
   
2. Mobilenet
   

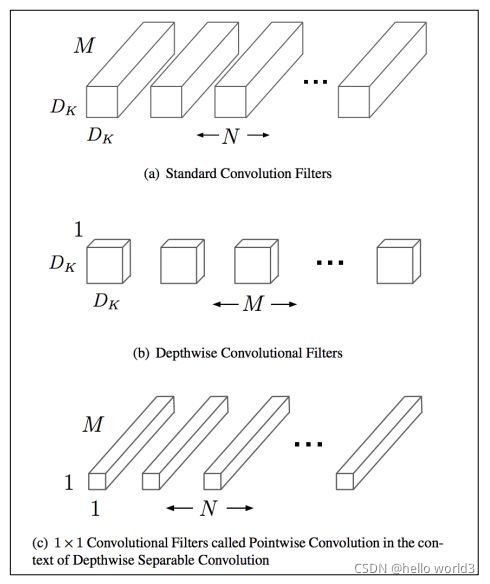
分解卷积

分解卷积，即将普通的kxk卷积分解为$k\times 1$和$1\times k$卷积，通过这种方式可以在感受野相同的时候大量减少计算量，同时也减少了参数量，在某种程度上可以看成是使用$2k$个参数模拟$k\times k$个参数的卷积效果，从而造成网络的容量减小，但是可以在较少损失精度的前提下，达到网络加速的效果。

BottleNeck结构

Bottleneck结构，主要是通过$1\times 1$卷积进行降维和升维，能在一定程度上能够减少计算量和参数量。其中$1\times 1$卷积操作的参数量和计算量少，使用其进行网络的降维和升维操作（减少或者增加通道数）的开销比较小，从而能够达到网络加速的目的。

神经网络搜索

神经结构搜索是一种自动设计神经网络的技术，可以通过算法根据样本集自动设计出高性能的网络结构，在某些任务上甚至可以媲美人类专家的水准，甚至发现某些人类之前未曾提出的网络结构，这可以有效的降低神经网络的使用和实现成本。

NAS的原理是给定一个称为搜索空间的候选神经网络结构集合，用某种策略从中搜索出最优网络结构。神经网络结构的优劣即性能用某些指标如精度、速度来度量，称为性能评估，可以通过NAS自动搜索出高效率的网络结构。

模型剪枝

结构复杂的网络具有非常好的性能，其参数也存在冗余，因此对于已训练好的模型网络，可以寻找一种有效的评判手段，将不重要的connection或者filter进行裁剪来减少模型的冗余。

剪枝的基本流程如下：

1. 正常流程训练一个神经网络，得到训练好的model
2. 确定一个需要剪枝的层，一般为全连接层，设定一个裁剪阈值或者比例。实现上，通过修改代码假如一个与参数矩阵尺寸一致的mask矩阵。mask矩阵只有0和1，实际上是用于重新训练的网络。
3. 重新训练微调，参数在计算的时候应该先乘以该mask，则mask位为1的参数值将继续通过BP调整，而mask位为0的部分因为输出始终为0则不对后续部分产生影响。
4. 输出模型参数存储的时候，因为有大量的稀疏，所以需要重新定义储存的数据结构，仅储存非0值以及矩阵位置。重新读取模型模型参数的时候，就可以还原矩阵。

神经网络的参数量往往非常多，而其中大部分的参数在训练好之后都会趋近于零，对整个网络的贡献可以忽略不计。通过剪枝操作可以使网络变得稀疏，需要存储的参数量减少，但是剪枝操作同样会降低整个模型的容量（参数量减少），在实际训练时，有时候会通过调整优化函数，诱导网络去利用模型的所有参数，实质上就是减少接近于零的参数量。最后，对于如何自动设定剪枝率，如何自适应设定剪枝阈值，在这里不做过多讨论。

核稀疏化

核的稀疏化，是在训练过程中，对权重的更新加以正则项进行诱导，使其更加稀疏，使大部分的权值都为0。核的稀疏化方法分为regular和irregular，regular的稀疏化后，裁剪起来更加容易，尤其是对im2col的矩阵操作，效率更高；而irregular的稀疏化会带来不规则的内存访问，参数需要特定的存储方式，或者需要平台上稀疏矩阵操作库的支持，容易受到带宽的影响，在GPU等硬件上加速并不明显。

量化操作

二值权重网络(BWN)是一种只针对神经网络系数二值化的二值网络算法。BWN只关心系数的二值化，并采取了一种混和的策略，构建了一个混有单精度浮点型中间值与二值权重的神经网络–BinaryConnect。BinaryConnect在训练过程中针对特定层的权重进行数值上的二值化，即把原始全精度浮点权重强行置为-1、+1两个浮点数，同时不改变网络的输入和层之间的中间值，保留原始精度。而真正在使用训练好的模型时，由于权重的取值可以抽象为-1、+1，因此可以采用更少的位数进行存放，更重要的是，很显然权重取值的特点使得原本在神经网络中的乘法运算可以被加法代替。乘法运算转变为加法的好处在于：计算机底层硬件在实现两个n位宽数据的乘法运算时必须完成2*n位宽度的逻辑单元处理，而同样数据在执行加法时只需要n个位宽的逻辑单元处理，因此理论上可以得到2倍的加速比。

由于BWN取得的成功，人们开始尝试对二值网络进行更加深入的研究改造，并试图从中获得更大的性能提升。其中，最重要的基础工作是Matthieu Courbariaux 等人在几个月后提出的二值神经网络(BNN)。这一方法在BWN的基 础上进一步加大二值化力度，进而完全改变了整个神经网络中的计算方式，将所需的计算量压缩到极低的水平。

BNN要求不仅对权重做二值化，同时也要对网络中间每层的输入值进行二值化，这一操作使得所有参与乘法运算的数据都被强制转换为“-1”、“+1”二值。我们知道计算机的硬件实现采用了二进制方式，而神经网络中处理过的二值数据 恰好与其一致，这样一来就可以考虑从比特位的角度入手优化计算复杂度。

BNN也正是这样做的：将二值浮点数“-1”、“+1”分别用一个比特“0”、“1”来表示，这样，原本占用32个比特位的浮点数现在只需1个比特位就可存放，稍加处理就可以实现降低神经网络前向过程中内存占用的效果。同时，一对“-1”、“+1”进行乘法运算，得到的结果依然是“-1”、“+1”，通过这一特性就可将原本的浮点数乘法用一个比特的位运算代替，极大的压缩了计算量，进而达到提高速度、降低能耗的目的。然而，大量的实验结果表明，BNN只在小规模数据集上取得了较好的准确性，在大规模数据集上则效果很差。

Song Han等人在量化神经网络(QNN)方面做了大量研究工作。这一网络的主要目的是裁剪掉数据的冗余精度，原本32位精度的浮点数由“1 8 23”的结构构成，裁剪的方法是根据预训练得到的全精度神经网络模型中的数据分布，分别对阶码和位数的长度进行适当的减少。实验证明，对于大部分的任务来说，6位比特或者8位比特的数据已经能够保证足够好的测试准确率。

QNN在实际的操作中通常有两种应用方式，一种是直接在软件层面实现整形的量化，通过更少的数据位数来降低神经网络在使用时计算的复杂度；另一种重要的应用是针对于AI专用芯片的开发。

由于芯片开发可以设计各种位宽的乘法器，因此将神经网络中32位的全精度数据可以被处理成6位或8位的浮点数，同时结合硬件指定的乘法规则，就可以在硬件上实现更高的运算效率，达到实时运行深度神经网络的目的。这也是QNN最大的理论意义。但是如果从软件角度而非硬件角度出发，只是将浮点数量化成整形数，就没有办法显著地降低计算复杂度（除非对整形再进行量化），也就无法达到在低配硬件环境上实时运行深度神经网络的目的。因此，在软件设计的层面上，QNN相比BNN并没有特别明显的优势。

Slimming

Sliming总体思路：实现一种channel-level的sparsity，就是在通道数上面稀疏化。本质是识别并剪掉那些不重要的通道(identify and prune unimportant channels)。

模型压缩可以在weight-level, kernel-level, channel-level 或者 layer-level上进行，为什么要在channel-level上面着手？weight-level往往需要特殊的硬件加速器或软件来实现fast inference。layer-level只适用于一些特别深的模型，比如超过50层的模型，但是不是很灵活。相比之下，channel-level 取得了灵活性和实现方便程度的折中。

首先我们可以给每个channel定义一个scaling factor $\gamma$，这个值在前向传播时要和这个channel的输出值乘在一起。在训练网络时，这个scaling factor $\gamma$与其他的权重一起训练，目标函数如下式：$$L=\sum _{x,y}l(f(x,W),y)+\lambda \sum _{x\in \tau }g(\gamma )$$只是为这个scaling factor $\gamma$加上了sparsity regularization的罚项。其中$(x,y)$代表正常的训练数据，$W$代表权重。在实验中取$g(s)=|s|$，即使用$L_1$范数。训练完后。把scaling factor$\gamma$比较小的channel视为是unimportant channel，可以剪掉。剩下的部分网络就是压缩后的网络，即compact model。所以，这个scaling factor$\gamma$的作用相当于是 an agent for channel selection。重要的是因为它们与网络联合优化，使得模型可以自动识别unimportant channel，可以安全地剪掉，而不影响性能。所以，有了这个scaling factor，就可以实现模型channel的压缩。

最后一个要解决的问题就是存在跨层连接的问题：有的网络(比如VGG, AlexNet)不存在跨层连接，但是像ResNet和DenseNet这种存在跨层连接的，就需要做一些调整。