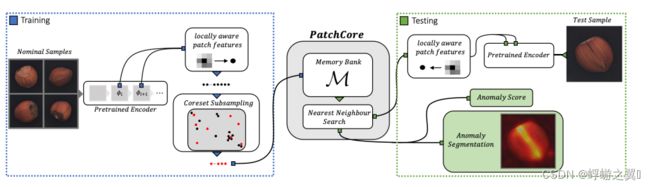
patchcore: Towards Total Recall in Industrial Anomaly Detection
patchcore论文地址
简介
略
算法
Locally aware patch features
样本用 x x x表示
label定义:0是正常样本(nominal),1是异常样本(anomalous)。 y x ∈ { 0 , 1 } y_x \in \{ 0 , 1\} yx∈{0,1}
训练阶段使用正常样本 : ∀ x ∈ X N : y x = 0 {\forall} x \in X_N : y_x=0 ∀x∈XN:yx=0
测试阶段样本: ∀ x ∈ X T : y x ∈ { 0 , 1 } {\forall x \in X_T : y_x \in \{0 ,1\}} ∀x∈XT:yx∈{0,1}
patchcore使用在ImageNet上的预训练网络,用符号 ϕ \phi ϕ表示
符号 ϕ i j = ϕ j ( x i ) \phi_{ij} = \phi_j(x_i) ϕij=ϕj(xi)表示第 i i i个样本 x i ∈ X x_i \in X xi∈X在网络 ϕ \phi ϕ第 j j j层feature map
本文使用ResNet50最终输出的spatial resolution blocks的第 j ∈ { 1 , 2 , 3 , 4 } j\in \{ 1,2,3,4\} j∈{1,2,3,4}层
采用网络最后几层输出会出现的问题:
- Firstly, it loses more localized nominal information [14].As the types of anomalies encountered at test time are not known a priori, this becomes detrimental to the downstream anomaly detection performance.
- very deep and abstract features in ImageNet pretrained networks are biased towards the task of natural image classification, which has only little overlap with the cold-start industrial anomaly detection task and the evaluated data at hand.
本文采用a memory bank M M M(在 patch level),避免过多的偏向imageNet
记第 i i i张图片,第 j j j层的特征图为 ϕ i j ∈ R c × h × w \phi_{ij} \in R_{c \times h\times w} ϕij∈Rc×h×w
特征图上的点用 ϕ i j ( h , w ) = ϕ j ( x i , h , w ) \phi_{ij}(h,w) =\phi_j(x_i,h,w) ϕij(h,w)=ϕj(xi,h,w)
each patch-representation operates on a large enough receptive
field size to account for meaningful anomalous context robust to local spatial variations.
本文采用感受野更大的patch(而不是特征图上的点)
This motivates a local neighbourhood aggregation when
composing each patch-level feature representation to increase receptive field size and robustness to small spatial deviations without losing spatial resolution or usability of feature maps.
记点 ( h , w ) (h,w) (h,w)周围的点集为:
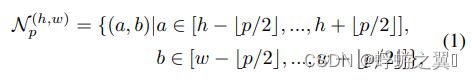
这个公式可以理解为 以 ( h , w ) (h,w) (h,w)为中心,以 p p p为直径的正方形包围住的点

那么围绕这些点计算的特征图上的点为
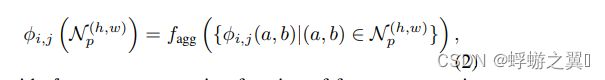
locally aware patch-feature collection 可以表示为:

其中 striding parameter: s
最后 PatchCore memory bank
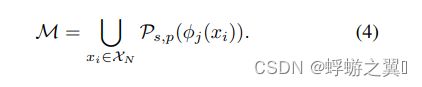
可以理解为 所有训练集的图片上所有的点 ( h , w ) (h,w) (h,w)
以这个点为中心计算它的邻居点集,得到的特征值
这些特征值的集合作为PatchCore memory bank
Coreset-reduced patch-feature memory bank
根据上面计算的PatchCore memory bank直接用是不现实的,因为太大了。所以需要计算一个 M C M_C MC(小一点的)d代替 M M M
什么样的子集能代替原来的集合呢?
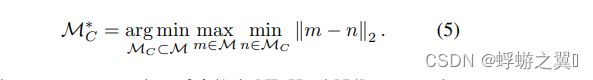
首先取任意一个子集 M C M_C MC
- 公式 min ∣ ∣ m − n ∣ ∣ 2 \min || m - n||_2 min∣∣m−n∣∣2 的含义:计算集合 M M M中每一个点 m m m到子集 M C M_C MC的距离
(一般点到集合的距离,定义为该点到集合内所有点的最小距离) - 公式 max \max max是指在 M M M中找到距离 M C M_C MC最大的点
- 最终求得距离集合 M M M最近的集合 M C ∗ M_C^* MC∗
Anomaly Detection with PatchCore
对于测试图片 x t e s t x^{test} xtest,计算测试图片的patch-feature 得到 m t e s t m^{test} mtest
和上面的过程一样,还是求集合 P ( x t e s t ) P(x^{test}) P(xtest)到集合 M M M的距离,标记距离的两个点为
m t e s t , ∗ ∈ P ( x t e s t ) , m ∗ ∈ M m^{test,*} \in P(x^{test}),m^*\in M mtest,∗∈P(xtest),m∗∈M
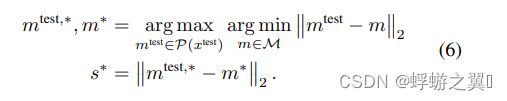
解释
- 公式 arg min ∣ ∣ m t e s t − m ∣ ∣ \argmin||m^{test}-m|| argmin∣∣mtest−m∣∣计算的是 点 m t e s t m^{test} mtest到集合 M M M的距离
- 然后找到距离最远的点 m t e s t , ∗ m^{test,*} mtest,∗
计算分数
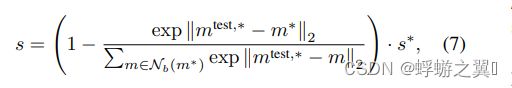
N ( m ) N(m) N(m)是指 m ∗ m^* m∗的最近邻点集,这里实际上是计算了 一个softmax