神经网络笔记
神经网络
一、 什么是神经网络
是基于生物学中神经网络的基本原理,在理解和抽象了人脑结构和外界刺激响应机制后,以网络拓扑知识为理论基础,模拟人脑的神经系统对复杂信息的处理机制的一种数学模型。
二、 神经网络的基本特性
(1) 非线性
非线性关系是自然界的普遍特性,人工神经元处于激活或抑制二种不同的状态,这种行为在数学上表现为一种非线性
(2) 非局限性
一个神经网络通常由多个神经元广泛连接而成。一个系统的整体行为不仅取决于单个神经元的特征,而且可能主要由单元之间的相互作用、相互连接所决定。通过单元之间的大量连接模拟大脑的非局限性。联想 记忆是非局限性的典型例子
(3) 非常定性
神经网络具有自适应、自组织、自学习能力。神经网络不但处理的信息可以有各种变化,而且在处理信息的同时,非线性动力系统本身也在不断变化。经常采用迭代过程描写动力系统的演化过程
(4) 非凸性
一个系统的演化方向,在一定条件下将取决于某个特定的状态函数。例如 能量函数,它的极值相应于系统比较稳定的状态。非凸性是指这种函数有多个极值(能有很多局部最优解),故系统具有多个较稳定的平衡态,这将导致系统演化的多样性(神经网络是一个非凸函数)
三、 神经元
人的大脑由非常多的神经元组成,每个神经元是接受信号和输出信号的最小单位。当我们人类接收外界信号时,这个信号会层层通过大脑里的神经元进行传递,最终这些会使得人类对外界做出一些反应。类似的,神经网络本身也是由大量的神经元(neuron)构成
神经元处理单元可表示不同的对象,例如特征、字母、概念,或者一些有意义的抽象模式。网络中处理单元的类型分为三类:输入单元、输出单元和隐单元。输入单元接受外部世界的信号与数据;输出单元实现系统处理结果的输出;隐单元是处在输入和输出单元之间
以下是一个神经元的工作结构

神经元的工作结构分为两个部分:
1、 Pre-activation
x1、x2、xd为各个输入,每个输入对于神经元都有对应的w权重参数,通过线性得出a(x),等于输入的线性累加后加上一个偏执b。
2、 Post-activation
最终的输出结果为g(x),是由a(x)做激活函数h(x),得出的g(x)
Pre-activation是一个线性结构,通过Post-activation非线性的激活函数后,得出的结果为非线性
由此可见,一个神经元的作用为就是:
计算输入向量和权重向量的内积,经过一个非线性传递函数得到一个标量
四、 激活函数
激活函数是负责将神经元的输入端映射到输出端的函数
激活函数分两种,一种是线性激活函数,一种是非线性激活函数
1、 线性激活函
线性激活函数实际上是没作用的,即便加了也等于什么都没加,因为它对信号不会做任何的处理。这有点类似于管道,来了信号之后原封不动地输出出去。之所以提出线性激活函数,其主要目的是为了完整性。那什么会用到线性激活函数呢?通常在,深度模型中的最后一层会用到。另外,如果我们没有叠加任何的激活函数到神经元,默认可以认为是加了线性激活函数。
如果你使用线性激活函数或者没有使用一个激活函数,那么无论你的神经网络有多少层一直在做的只是计算线性函数,所以不如直接去掉全部隐藏层。
2、 非线性激活函数
非线性的激活函数能,加强网络的表示能力,解决线性模型无法解决的问题
常见的激活函数
(1) Sigmoid

将我们的输入映射到0到1之间
如果输入的值非常大,我们能通过Sigmoid将输入映射到0到1之间,从而给下一层神经元作为输入计算,当下一层的神经元计算出来后的值也很大,也通过这样方式。
(2) Tanh

将我们的输入映射到1到-1之间
五、 多层神经网络
当我们增加额外的隐含层时就可以得到多层神经网络。至于隐含层的个数是没有限制的,我们可以随意搭建很多层的神经网络。为什么要增加隐含层呢?道理很简单,增加隐含层可直接导致模型的复杂度变高,随之带来的就是可以学出xx到yy的更复杂的映射关系

L层为隐含层
Output为最后输出层,最后的输出层的激活函数根据神经网络的使用场景来调整,如上图输出层最后做了softmax,再输出给损失函数loss
Softmax:又称归一化指数函数,作用是把输入转化成概率。softmax的公式如下:

Xi是当前输入的第i个数值,Xj是累计输入
他能够保证:
1)所有的值都是 [0, 1] 之间的(因为概率必须是 [0, 1])
2)所有的值加起来等于 1
六、 损失函数
任何模型训练的第一步是明确损失函数。模型训练过程无非就是在优化损失函数,从而找到让损失函数最小的模型的参数
损失函数是衡量网络输出合真实值的差异
损失函数并不使用测试数据来衡量网络的性能
损失函数用来指导训练过程,使得网络的参数向损失降低的方向改变
假设我们的神经网络用作分类,损失函数定义为交叉熵损失函数,当神经网络的输出层做了softmax,输出当前的输入,对应各个类别的概率,选取概率最高的类别,最后再通过交叉熵损失函数来检测当前神经网络输出的类别与真实标签的类别是否一致,从而反向调整网络
交叉熵误差(cross_entropy_error):

log表示以e为底数的自然对数(log e)。yk是神经网络的输出,tk是正确解标签。并且,tk中只有正确解标签的索引为1,其他均为0(one-hot表示)。
交叉熵误差的值是由正确解标签所对应的输出结果决定的。
只计算神经网络最终输出真实类别标签的损失,其余的不计算。
假设最终输出三个类别,三个概率分别是,x1是0.5,x2是0.2,x3是0.3,我们的输入标签是y2,那么交叉熵只对x2进行损失计算,将0.2带入损失函数中进行计算,得到的值,我们希望该值越小越好,通过优化算法反向调整网络参数,进而将输出x2的概率变高。
七、 优化算法
当我们有了损失函数后,接下来我们就可以通过优化算法去学习参数,优化算法中最经典的就是梯度下降法
梯度下降法:
一种求解最优化的算法。其中心思想是沿着目标函数梯度的方向更新参数值以希望达到目标函数最小
我们可以想象我们深处高山上的某一处位置,而梯度下降法,就是帮助我们到达山底的方法。当我们不知道自身所处在山的具体位置时,我们可以通过查看最陡峭的下坡路寻找到最快到达山底的路,每走一段距离,我们将重新测试山坡的梯度。通过迭代的方式(反复测量和行走)直到到达山底,显然这是下山的最短路径。
在机器学习中我们可以将初始位置当作是输入到预测函数的初始值,同时也对应损失函数上的某个起始点。山体的陡峭程度则是梯度,对应于损失函数的导数或偏导数。以测量最陡路径次数作为迭代次数,那么在一次迭代中所走的下坡路的路径则与学习率密切相关。通过一定次数的迭代,当我们走到山脚时,如果此山峰只有山脚这一个低谷,那么这个山脚就对应于损失函数的最小值。如下图所示。所以梯度下降法的目的就是寻找到损失函数的最小值
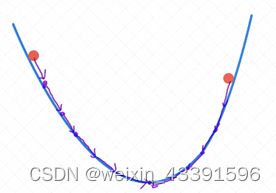
需要注意的一点是:梯度下降法依赖于求导,这也是为什么对函数的求导能力如此重要!
对于梯度下降法来说,有一个重要的参数叫作学习率(learning rate)(上图的n), 我们可以把它看作是可调节的参数(也称之为超参数)。学习率对于收敛以及对最终的结果起到很重要的作用。
当我们学习率比较小时,收敛会比较慢。当我们的学习率很大时,算法不稳定,可能不收敛
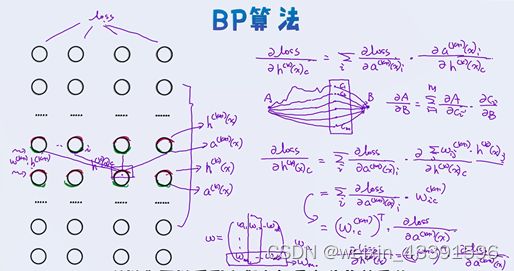
八、 反向传播算法(bp)与前向传播
1、 前向传播
神经网络从输入层开始,经过一层层的隐含层,不断计算每一个隐含层的神经元的结果,最终的到一个输出得过程。
当我们进行前向传播时,每一层的参数可以是随机的,也可以时预训练得到的,最后通过反向传播来调整每一层的参数
2、 反向传播
前向传播计算出了输出值(也即预测值),就可以根据输出值与目标值的差别来计算损失loss
反向传播就是根据损失函数loss来反方向地计算每一层的偏导数,从最后一层逐层向前去改变每一层的权重,也就是更新参数,核心就是损失函数对每一网络层的每一个参数求偏导的链式求导法则。
反向传播的计算过程:

反向传播算法总共可分为五个部分
1、 loss损失函数对输出层的输出进行梯度求导
2、 loss损失函数对输出层的输入进行梯度求导
3、 loss损失函数对各个隐含层的输出进行梯度求导
4、 loss损失函数对各个隐含层的输入进行梯度求导
5、 loss损失函数对各个层的W权值和b偏执进行求导
各个部分的梯度求导如下
我们假设使用的交叉熵做损失函数,softmax做输出层的激活函数来进行分析
(1) loss损失函数对输出层的输出进行梯度求导

我们先对其中一个f(x)c进行计算,已知我们的损失函数使用的是交叉熵,输出层最后一层激活函数使用的是softmax,计算如下:
只有当f(x)c输出的类型,与真实标签类型一致,才会进行梯度求导,否则都为0
最终对输出层所有梯度求导,整合成一个向量e(y)
反向传播进行求导时,每一层都有依赖性,某一层会依赖上一层的求导。所以方向传播是从loss损失函数反向进行由下到上求导,而不是从输入层由下到上进行求导