【CV & Unity】仿射变换原理

什么是仿射变换？

仿射变换（Affine Transformation）是空间直角坐标系的变换，从一个二维坐标变换到另一个二维坐标，仿射变换是一个线性变换，他保持了图像的“平行性”和“平直性”，即图像中原来的直线和平行线，变换后仍然保持原来的直线和平行线，仿射变换比较常用的特殊变换有平移(Translation)、缩放（Scale）、翻转（Flip）、旋转（Rotation）和剪切(Shear)。

线性变换和仿射变换的差别

线性变换	仿射变换
变换前是直线的，变换后依然是直线直线比例保持不变变换前是原点的，变换后依然是原点	变换前是直线的，变换后依然是直线直线比例保持不变

线性变换和仿射变换的差别在原点是否改变

空间变换的两个主要类别

仿射变换

仿射变换：平移、旋转、放缩、剪切、反射

仿射变换的公式表达

$\left(\begin{array}{c}{X}_2\\ Y_2\\ 1\end{array}\right)=\left[\begin{array}{ccc}{A}_{11}& A_{12}& B_{11}\\ A_{21}& A_{22}& B_{12}\\ 0& 0& 1\end{array}\right]\times \left(\begin{array}{c}{X}_1\\ Y_1\\ 1\end{array}\right)$

通过上述的矩阵转换可以将图像进行平移、缩放、旋转和剪切，如下图所示

仿射变换在ML机器学习领域的应用

仿射变换的思想在机器学习“图像处理”领域对应单应性矩阵

在三轴坐标中$XYZ，Z=1$这个有点类似于三维的齐次坐标。单应性矩阵主要用来解决两个问题，

1. 表述真实世界（Unity中的主世界相机视角）中一个平面与对应它图像的透视变换
2. 从通过透视变换实现图像从一种视图变换到另外一种视图
   

上图的中零点分别表示两个平面中任意两个点，a1、a2与b1、b2是这两点对应的两个方向上的线性向量。对于这两个平面之间的关系，我们可以通过这些点从而一步确定两个平面直接的关系，而两个平面之间的关系用单应性矩阵来描述如下：
$p^h=H{q}^h$
其中，$-p^h，q^h$表示三维的齐次坐标向量
这种关系被称为平面单应性。这个当中有一些数学知识推导，这里不做证明，只是明白这个概念怎么来的。

• 此外两个计算机图形学的应用场景分布是纹理渲染与计算平面阴影。
• 用来实现图像拼接时候解决对齐问题

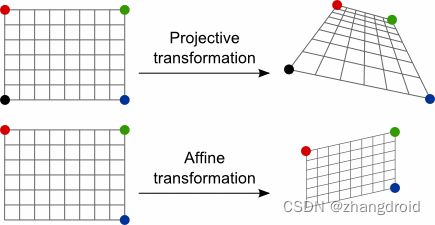
投影变换

$\left(\begin{array}{l}{x}_1^t\\ x_2^t\\ x_3^t\end{array}\right)=\left[\begin{array}{lll}{h}_{11}& h_{12}& h_{13}\\ h_{21}& h_{22}& h_{23}\\ h_{31}& h_{32}& h_{33}\end{array}\right]\left(\begin{array}{l}{x}_1\\ x_2\\ x_3\end{array}\right)$
投影和仿射变换之间的区别

投影变换	仿射变换
变换前是直线的，变换后依然是直线直线比例改变变换前平行的两条线，变换后不一定平行	变换前是直线的，变换后依然是直线直线比例改变变换前平行的两条线，变换后不一定平行

这些仿射变换和投影变换之间的唯一区别在于变换矩阵的最后一行。对于仿射变换，该行的前两个元素为零。这导致操作属性存在以下差异：

• 投影变换不保留平行度、长度和角度。

• 仿射变换与投影变换不同，保留了并行性。

射影变换可以表示为任意四边形（即四点系统）到另一个四边形的变换。仿射变换是三角形的变换。下图说明了这一点：

直观的例子：

仿射变换：

仿射变换C#代码实现

在Graphics Mill中应用仿射变换，请执行以下步骤：

1. 指定源和目标三角形。

2. 使用Matrix.CreateFromAffinePoints(PointF[], PointF[])创建仿射变换矩阵。将先前指定的点作为方法参数传递。

3. 使用MatrixTransform.#ctor构造函数创建转换。这里之前创建的矩阵是构造函数的参数。

4. 通过调用MatrixTransform.Apply方法应用转换。

   using (var bitmap = new Bitmap(@"Images\in.jpg"))
  {
    System.Drawing.PointF[] source = {
        new System.Drawing.PointF(0f, 0f),
        new System.Drawing.PointF(0f, 80f),
        new System.Drawing.PointF(80f, 0f)
    };
    


    System.Drawing.PointF[] target = {
        new System.Drawing.PointF(20, 0f),
        new System.Drawing.PointF(0f, 80f),
        new System.Drawing.PointF(80f, 0f)
    };

    using (var matrix = Matrix.CreateFromAffinePoints(source, target))
    {
        using (var transform = new MatrixTransform(matrix))
        {
            using (var result = transform.Apply(bitmap))
            {
                result.Save(@"Images\Output\out.jpg");
            }
        }
    }
}

投影变换：

投影变换C#代码实现

在Graphics Mill中应用投影变换，请执行以下步骤：

1. 指定源四边形和目标四边形。
2. 使用Matrix.CreateFromProjectivePoints(PointF[], PointF[])创建投影变换矩阵。将先前指定的点作为方法参数传递。
3. 使用MatrixTransform.#ctor构造函数创建转换。这里之前创建的矩阵是构造函数的参数。
4. 通过调用MatrixTransform.Apply方法应用转换。

 
using (var bitmap = new Bitmap(@"Images\in.jpg"))
{
    System.Drawing.PointF[] source = {
        new System.Drawing.PointF(0f, 0f),
        new System.Drawing.PointF(0f, bitmap.Height),
        new System.Drawing.PointF(bitmap.Width, bitmap.Height),
        new System.Drawing.PointF(bitmap.Width, 0f)
    };

    System.Drawing.PointF[] target = {
        new System.Drawing.PointF(0f, 0f),
        new System.Drawing.PointF(0f, bitmap.Height),
        new System.Drawing.PointF(bitmap.Width * 0.75f, bitmap.Height - 50f),
        new System.Drawing.PointF(bitmap.Width * 0.75f, 80f)
    };

    using (var matrix = Matrix.CreateFromProjectivePoints(source, target))
    {
        using (var transform = new MatrixTransform(matrix))
        {
            using (var result = transform.Apply(bitmap))
            {
                result.Save(@"Images\Output\out.jpg");
            }
        }
    }
}

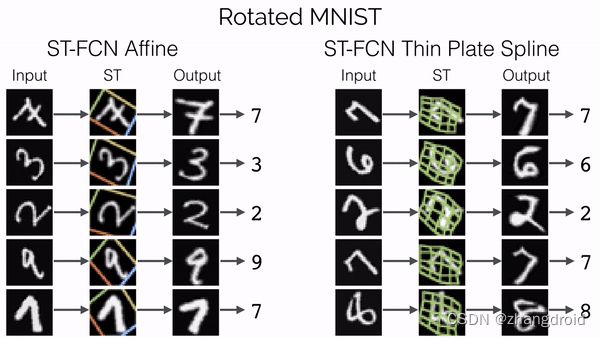
仿射变换在机器学习中的应用

在用CNN模型处理MINST手写数据集的识别中，引入了仿射变换的方法提升了识别准确性
论文：https://arxiv.org/abs/1506.02025

参考资料：

仿射和投影变换 - Graphics Mill
Review: STN — Spatial Transformer Network (Image Classification)
如何通俗地讲解「仿射变换」这个概念？ - 马同学的回答 - 知乎