Mathematica学习笔记

本文用于记录Mathematica学习中遇到的小问题

1. Mathematica在给出初始聚类中心的情况下进行Kmeans聚类

为了避免kmeans得到局部最优解，最好使用随机种子，这里指定聚类中心只适用于特殊情况
如：需要确定的聚类结果等
吐槽一下，Mathmatica果然社区还是没有MATLAB完善啊，这个问题我在MATLAB能搜到但是Mathmatica搜不到，当然也有这个问题太简单的原因

首先上结论，使用Method -> {"KMeans", "InitialCentroids" -> {{0, 4}, {3, 3}}来指定初始聚类中心，相关内容文档有，不过就一行我没注意

---

下面是简单的实验-----是否指定初始聚类中心造成的结果变化（没什么内容，没必要看）
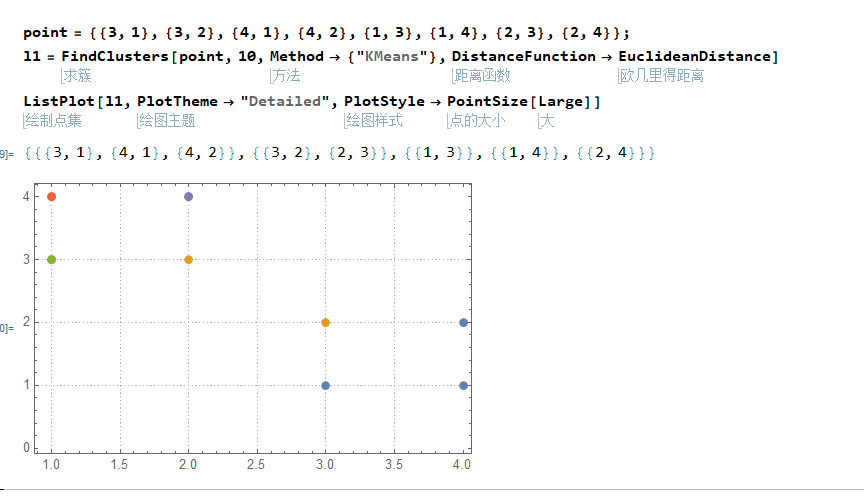
使用Kmeans 欧几里得距离 聚类上限10 不指定初始聚类中心 进行聚类

point = {{3, 1}, {3, 2}, {4, 1}, {4, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 
    4}};
l1 = FindClusters[point, 10, Method -> {"KMeans"}, 
  DistanceFunction -> EuclideanDistance]
ListPlot[l1, PlotTheme -> "Detailed", PlotStyle -> PointSize[Large]]

可以发现，整整聚类出了5个结果，显然不是我们想要的效果，那么下面指定初始聚类中心
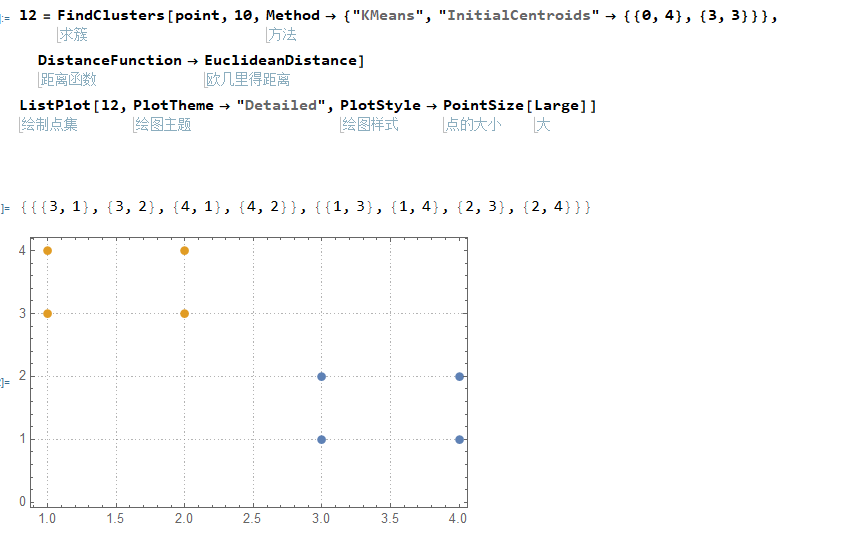
使用Method -> {"KMeans", "InitialCentroids" -> {{0, 4}, {3, 3}}来指定初始聚类中心

l2 = FindClusters[point, 10, 
  Method -> {"KMeans", "InitialCentroids" -> {{0, 4}, {3, 3}}}, 
  DistanceFunction -> EuclideanDistance]
ListPlot[l2, PlotTheme -> "Detailed", PlotStyle -> PointSize[Large]]

聚出两类，符合预期效果

2.根据llist1的值选取等长list2中的值

• Pick[list,sel]
  从列表 list 中选取符合条件的元素，其对应于 sel 中的元素为 True.
• Pick[list,sel,patt]
  从列表 list 中选取符合条件的元素，其对应于 sel 中的元素匹配 patt.

//选取True
Pick[{{3, 1}, {3, 2}, {4, 1}, {4, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 
   4}}, {True, True, True, True, False, False, True, True}]
//选取指定数据
Pick[{{3, 1}, {3, 2}, {4, 1}, {4, 2}, {1, 3}, {1, 4}, {2, 3}, {2, 
   4}}, {True, True, True, True, False, False, True, True}, False]

3. 比较两个等长list，输出一个由true/false组成的list

• Thread[f[args]]
  将 f 线性作用（thread over）于任意出现在 args 中的列表.
• Thread[f[args],h]
  将 f 线性作用于出现在 args 中的头部为 h 的任何对象上.
• Thread[f[args],h,n]
  将 f 线性作用于出现在前 n 项 args 中的头部为 h 的对象上.

tmp1
tmp2
bool = Thread[tmp1 > tmp2]