机器学习-K近邻算法
K近邻算法
- 算法思想
-
- 算法模型
-
- 算距离公式
- 手写代码
k-NN 算法(k-Nearest Neighbor),也叫 k 近邻算法。
学会 k-NN 算法,只需要三步:
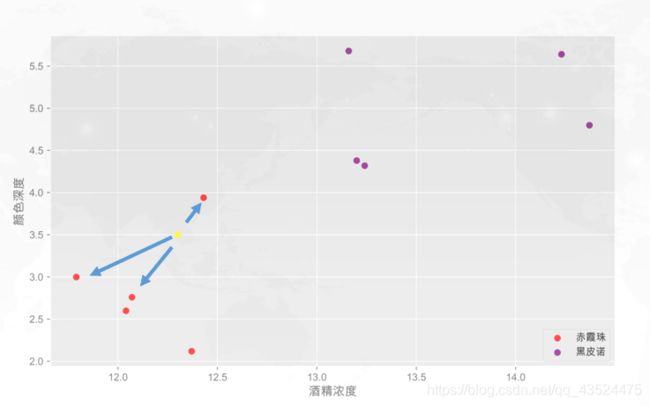
其实K-NN算法,可以用中国的古话来理解就是:“远亲不如近邻”,比如说,在上面的散点图模型中,我们大致了解到两种酒的散点区域,当我们重新输入一个数据的时候,就是图中的黄点,黄点就是代表机器就要判别的酒,点的颜色既不是我们知道的红色也不是紫色,但是我们发现到,这个点离附近的3个红点最近,所以红点和紫色类别的投票数是3:0,红色取胜,所以黄色点属于红色,也就是新的一杯属于「赤霞珠」。
这里我们知道一共的投票数,是3票,其实我们也可以设置为4票,6票,票数越多,其实我们可以判断的越精准。
算法思想
这就是k-近邻算法,它的本质是通过距离判断两个样本是否相似,如果距离够近就认为他们足够相似属于同一类别。
当然只对比一个样本是不够的,误差会很大,我们需要找到离其最近的k个样本,并将这些样本称之为「近邻」(nearest neighbor)。对这k个近邻,查看它们的都属于何种类别(这些类别我们称作「标签」(labels))。
然后根据**“少数服从多数,一点算一票”原则进行判断,数量最多的的标签类别就是新样本的标签类别。其中涉及到的原理是“越相近越相似”**,这也是KNN的基本假设。
其实这样很像概率统计的思想,讲求的是可能性,而不是确定性。
算法模型
在了解算法模型之前,我们先了解一下几个小概念
- 训练集:确定模型后,用于训练的数据集,就比如说我们已经知道酒的特征就可以构建出一个训练集
- 测试集:可以理解为没有参与训练的数据集,我们要测试机器的判断的结果是否正确,就比如说等待判别的酒(图中的黄点)
- 验证集:用训练集对模型训练完毕后,再用验证集对模型测试,测试模型是否准确而不是训练模型的参数
可以看到k-近邻算法就是通过距离来解决分类问题。这里我们解决的二分类问题,整个算法结构如下:
-
算距离
给定测试对象 Item,计算它与训练集中每个对象的距离。
依据公式计算 Item 与 D_1,D_2, ……D_j之间的相似度,得到Sim(Item,D_1), Sim(Item,D_2), Sim(Item,D_j) -
找邻居
圈定距离最近的k个训练对象,作为测试对象的近邻。
将Sim(Item,D_1), Sim(Item,D_2), Sim(Item,D_j)排序,若是超过相似度阈值t,则放入邻居集合NN -
做分类
根据这k个近邻归属的主要类别,来对测试对象进行分类。
自邻居集合NN中取出前k名,查看它们的标签,对这k个点的标签求和,以多数决,得到Item可能类别。
k-NN算法基本思想我们已经知道了,其模型的表示形式是整个数据集。除了对整个数据集进行存储之外,k-NN没有其他模型。因此,k-NN不具有显式的学习过程,在做「分类」时,对新的实例,根据其 k 个最近邻的训练实例的类别,通过多数表决等方式进行预测。k-近邻法实际上利用了训练数据集对特征向量空间进行划分,并作为其分类的 “模型” 。
那么问题来了,我们有一种感觉,就是K-NN算法中很重要的一步就是算距离,该算法的「距离」在二维坐标轴就表示两点之间的距离,计算距离的公式有很多,我们常用欧拉公式,即“欧氏距离”。
算距离公式
空间中 A 和 B 两个点,它们的距离等于 x 和 y 两坐标差的平方和再开根号。

如果在三维坐标中,多了 z 坐标,距离计算公式也相同。

哎,以上两个小公式,帮助我们想起了在N维空间下的距离公式,可是我们知道一个物体的特征,其实并不是简单的几个,比如说,一个酒的特征不仅仅有酒精浓度,颜色深度两个特征,还可以有发酵时间,酒精甜度等多个特征的。
当特征数量有很多个形成多维空间时,再用上述的写法就不方便了,我们换一个写法,用 X 加下角标的方式表示特征维度。则在n维空间中,有两个点 A 和 B,它们的坐标分别为:

则A和B两点之间的欧氏距离的基本计算公式如下:

而在我们的机器学习中,坐标轴上的值 x_1,x_2,…… x_n 正是我们样本数据上的n个特征。
手写代码
这就是 k-NN 算法的数学原理,似不似也很简单?
只要计算出样本点与样本集中的每个样本的坐标距离,然后排序筛选出距离最短的 k 个点,统计这 k 个点所属类别,数量占多的就是新样本所属的酒类。
根据欧拉公式,我们可以用很基础的 Python 代码实现~
# 先导入包
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
sklearn是一个python的通用机器学习库,稍后的文章会介绍,在机器学习中这个库会经常用到的。
模拟出一些数据集出来
#r = np.random.randint(1,100)
r = 4
#print(r)
x , y = make_blobs(n_samples = 50, # 生成了50个样本
centers = [[0,0],[1,1],[-1,1]] # label的种类数,生成了3个类别
cluster_std = [0.3, 0.3, 0.3], # 50个分成3个类别,每个类别的方差为0.3,方差越大,特征越分散。
,random_state = r # 设置了一个随机种子
) # make_blobs函数见下方链接
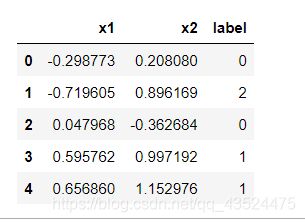
sim_data = pd.DataFrame(x, columns = ['x1', 'x2']) # 将x的数据分为了两个列x1和x2
sim_data['label'] = y #在DataFrame加入新的lable列,值为y值,因为分为3类,所以lable值分别为0,1,2
sim_data.head(5) # 查看前5行的内容
datasets = sim_data.copy() # 将DataFrame复制给datasets
# 设置测试点
p = [0, 0]
plt.scatter(sim_data['x1'], sim_data['x2'], c = y) # 样本集的散点图
plt.scatter(p[0], p[1], c = 'red', marker = 'x') # 测试点在散点图中的位置
plt.show() # 将图片展示出来
关于上述代码的部分解释:
- sklearn中的make_blobs的用法
# 计算每一个点到测试点距离的平方
X = datasets.iloc[:,:-1] # 将datasets的前两列的内容切片出来给X
y = datasets.iloc[:, -1] # 将datasets的最后一列的内容切片出来给y
d = np.power(X - p, 2).sum(axis = 1)
# power()用于数组元素求n次方
# axis的重点在于方向,而不是行和列。1表示横轴,方向从左到右;0表示纵轴,方向从上到下。
# 把计算出来的距离与标签拼接起来
df_dist = pd.DataFrame({'dist' : d, 'label' : y}) # 构建出了一个新的DataFrame,
# 确认前k个点
k = 3
# 开始投票
df_dist.sort_values(by = 'dist').iloc[:k, -1].mode().values[0] # sort_values() 默认升序排序,iloc实现切片,mode()提取众数,也就是票数最多
那么根据上方的代码的一个逻辑,其实我们已经大致实现了K–NN的算法思想,算距离→排序→投票,但是我们知道,总不能用一次代码,就在重新写一次吧,不防我们写一个函数,把方法封装进去。
#r = np.random.randint(1,100)
r = 4
#print(r)
x , y = make_blobs(n_samples = 50, # 生成了50个样本
centers = [[0,0],[1,1],[-1,1]] # label的种类数,生成了3个类别
cluster_std = [0.3, 0.3, 0.3], # 50个分成3个类别,每个类别的方差为0.3,方差越大,特征越分散。
,random_state = r # 设置了一个随机种子
) # make_blobs函数见下方链接
sim_data = pd.DataFrame(x, columns = ['x1', 'x2']) # 将x的数据分为了两个列x1和x2
sim_data['label'] = y #在DataFrame加入新的lable列,值为y值,因为分为3类,所以lable值分别为0,1,2
# 把上面的代码逻辑封装成一个函数
def knn_classify(p, datasets, k): # 将测试点,样本集,需要排序的前k个点设置为参数
X = datasets.iloc[:,:-1]
y = datasets.iloc[:, -1]
d = np.power(X - p, 2).sum(axis = 1)
df_dist = pd.DataFrame({'dist' : d, 'label' : y})
predict = df_dist.sort_values(by = 'dist').iloc[:k, -1].mode().values[0]
return predict # 这样返回的就是 一个众数
# 测试
knn_classify(p = [-1,1], datasets = datasets, k = 5)