吴恩达深度学习深度学习概述以及优化

---

1、深度学习概述

在之前的吴恩达机器学习课程中，举了一个预测房屋价格的例子，当时的输入变量只有房屋面积，对于这种问题当时的解决方案是单变量线性回归，当时的假设函数是$y=ax+b$，其实这个问题也可以看做一个最简易的神经网络的问题，如下图所示。

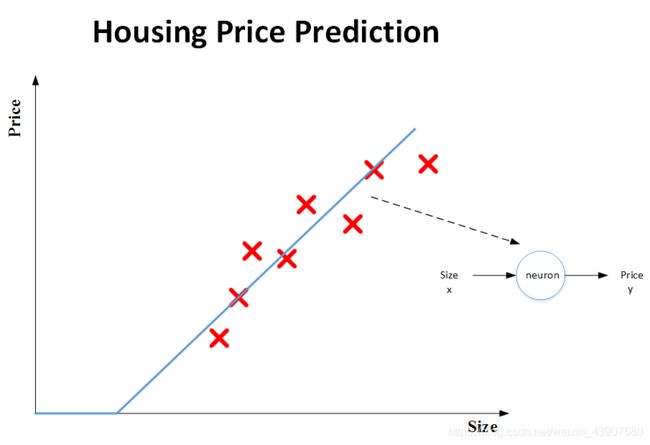
该神经网络的输入x是房屋面积，输出y是房屋价格，中间包含了一个神经元（neuron），即房价预测函数（蓝色折线）。该神经元的功能就是实现函数f(x)的功能。

现在对于这个进行复杂化，增加输入变量的特征值，如下图所示，构建一个两层的神经网络。

2、神经网络基础之逻辑回归

在学习机器学习的课程时已经做过记录，这里不在重复。

3、深层神经网络

一般命令规则上，1个隐藏层的神经网络叫做2 layer NN，2个隐藏层的神经网络叫做3 layer NN，以此类推。如果是L-layer NN，则包含了L-1个隐藏层，最后的L层是输出层。例如，以下是一个四层的神经网络图。

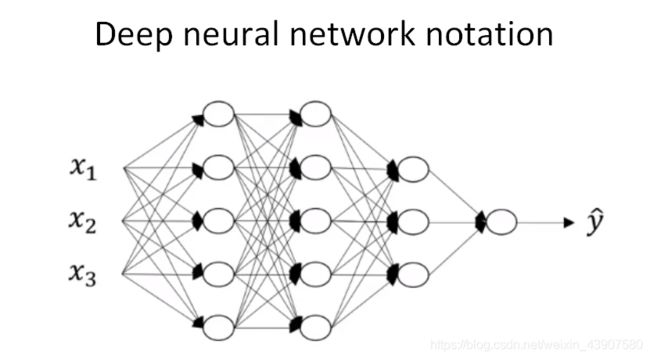
有关神经网络的前向传播和反向传播公式及推导之前有过记录，这里不在重复

4、深度学习实用层面

4.1 训练集、验证集、测试集

Train sets用来训练算法模型；Dev sets用来验证不同算法的表现情况，从中选择最好的算法模型；Test sets用来测试最好算法的实际表现，作为该算法的无偏估计。

训练集用来训练我们的模型，比如调整神经网络中的$w$参数。验证集用来挑出一个表现最好的模型，比如说调整一些超参数，比如训练轮数。测试集用来测试我们训练好的模型。三个数据集尽量不重复

三个数据集的设置比例大概是60%、20%、20%，如果样本数较大，可以提高训练集比例，比如100万样本，可以设置为98%、1%、1%

4.2 偏差、方差

Bias和Variance是对立的，分别对应着欠拟合和过拟合。如下图所示，显示了二维平面上，high bias，just right，high variance的例子。

我们用以下的靶心图进行解释。

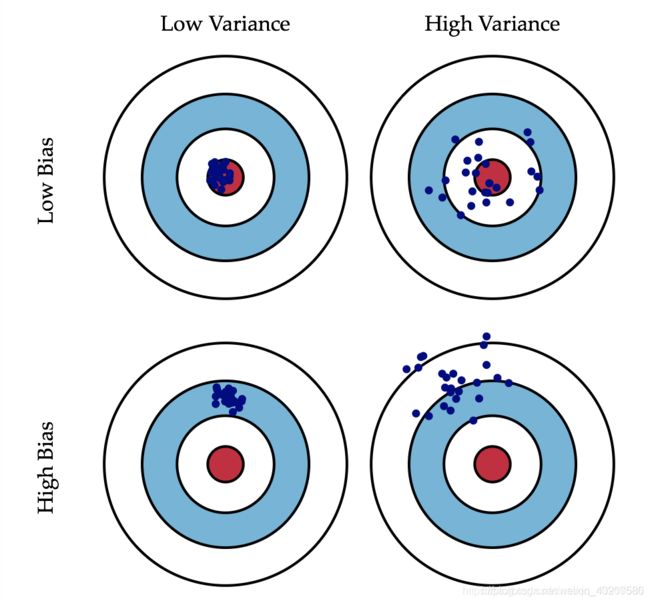
靶心对应理想状态下最优的训练模型，而蓝点表示我们自己训练的模型运行的结果，左上第一个图表示训练模型比较好，右上的图表示当模型跑不同的数据集时动荡的幅度较大，这就意味着该模型泛化能力差，即过拟合，做下的图表示偏差较大，即欠拟合。

4.3 L1、L2正则化

如果出现了过拟合，可以采用正则化来解决。L2 regularization的表达式为：
$$J=\frac{1}{m}\sum _{i=1}^{m}L(y^{(i)},y^{(i)})+\frac{\lambda }{2m}||w|{|}^2$$
L1 regularization的表达式为：$$J=\frac{1}{m}\sum _{i=1}^{m}L(y^{(i)},y^{(i)})+\frac{\lambda }{2m}||w||$$与L2 regularization相比，L1 regularization得到的w更加稀疏，即很多w为零值。其优点是节约存储空间，因为大部分w为0。然而，实际上L1 regularization在解决high variance方面比L2 regularization并不更具优势。而且，L1的在微分求导方面比较复杂。所以，一般L2 regularization更加常用。

从单一感性的角度来分析L1和L2正则化，附上一张图

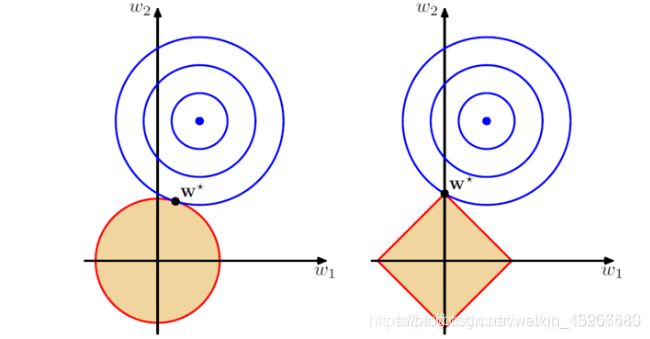
蓝线表示上面正则表达式的前段，红线表示正则表达式的后段，红线和蓝线的交点表示结合正则化的最优解，由图所示，L1正则表达式会产生0参数，从而产生稀疏解。

理论推导可参考 https://blog.csdn.net/b876144622/article/details/81276818

4.4 归一化处理

标准化输入就是对训练数据集进行归一化的操作，即将原始数据减去其均值μ后，再除以其方差σ2：$$\mu =\frac{1}{m}\sum _{i=1}^m{X}^{(i)}$$
$${\sigma }^2=\frac{1}{m}\sum _{i=1}^m(X^{(i)}{)}^2$$
$$X=\frac{X-\mu }{{\sigma }^2}$$
归一化过程如下图所示

之所以要对输入进行标准化操作，主要是为了让所有输入归一化同样的尺度上，方便进行梯度下降算法时能够更快更准确地找到全局最优解

4.5 Dropout

Dropout是指在深度学习网络的训练过程中，对于每层的神经元，按照一定的概率将其暂时从网络中丢弃。也就是说，每次训练时，每一层都有部分神经元不工作，起到简化复杂网络模型的效果，从而避免发生过拟合。

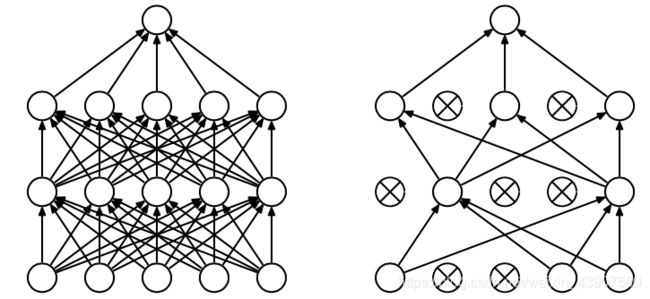
对于某个神经元来说，某次训练时，它的某些输入在dropout的作用被过滤了。而在下一次训练时，又有不同的某些输入被过滤。经过多次训练后，某些输入被过滤，某些输入被保留，对于某一个神经元来说，不依赖于任何一个特征，也就是说，对应的权重w不会很大。这从从效果上来说，与L2 regularization是类似的，都是对权重w进行“惩罚”，减小了w的值

4.6 其他正则化方法

增加训练样本可以防止过拟合，但是这一过程较为困难，因此我们可以在原样本的基础上对他进行相应的改变，有一个样本变成多个样本，比如：

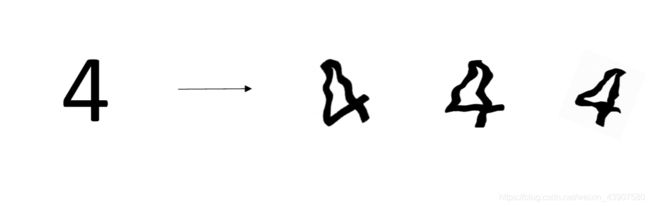
4.7 梯度消失和爆炸

当训练一个 层数非常多的神经网络时，计算得到的梯度可能非常小或非常大，甚至是指数级别的减小或增大。这样会让训练过程变得非常困难。
假设（假设每一层只有一个神经元，其中激活函数为sigmoid函数），如图：

则根据反向传播链式法则：

而对sigmoid函数求导后最大值也是0.25，而初始化w也是通常小于1，因此多个小于1的数连乘之后，那将会越来越小，导致靠近输入层的层的权重的偏导几乎为0，也就是说几乎不更新，这就是梯度消失。
如果 ${\sigma }^{\prime }(z)w>1$时，连乘下来就会导致梯度过大，导致梯度更新幅度特别大。

下面讨论解决方案：

改变激活函数

tanh函数：

比sigmoid的好一点，sigmoid的最大值小于0.25，tanh的最大值小于1，但仍是小于1的，所以并不能解决这个，但还是比sigmoid函数好。

Relu函数:


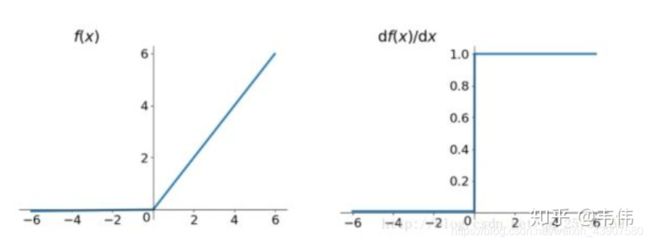
relu函数的导数在正数部分是恒等于1的，因此在深层网络中使用relu激活函数就不会导致梯度消失和爆炸的问题。

但是由于负数部分恒为0，会导致一些神经元无法激活（可通过设置小学习率部分解决）

leakrelu函数

其中k是leak系数，一般选择0.1或者0.2，leakrelu解决了0区间带来的影响，而且包含了relu的所有优点。

其他的改善的方法可参考梯度消失及爆炸