一致性校正方法2
长短帧方法,本人借鉴于某些摄像头厂家,类似于区域检测,以及警戒区域安保识别等范例。具体是通过建立短帧(一般为连续相邻帧),长帧(间隔一定时间的帧)进行识别过程。
具体在一致性校正处理过程中,当设备成像过程不稳定,导致成像图像出现局部灰度拉伸,全局对比度失真等情况时,一般进行样张多拍,在多样张中首先将两两相邻的图像设立为短帧,间隔5张图像设立为长帧。通过长短帧的均值差异建立权重,最终进行带权重的均值过程,实现单张图像的校准过程。
长短帧校准基础原理如下:
clear;clc;close all
infiles='V2mean\combine\';
files12='V2mean\combineV1\';
n=360;
long=zeros();%设定长帧变量
short=zeros();%设定短帧变量
for k=1:n
img1 = double(imread([infiles,num2str(k),'.jpg']));%文件所在路径
short(k)=mean(mean(img1));
i=ceil(k/5);
long(i)=mean(mean(img1));
end在解决这个问题时,我首先也是采集多幅样张,然后直接求均值,导致的结果就是单张极值出现问题的时候,整体求解将会在灰度上有偏移。
所以本人在求解时,首先对每张图像进行中位数和灰度平均值进行获取,采用线性关系,按照0.7中位数+0.3灰度平均值,再除以所求图像张数n作为权重,进行灰度值求取。该方法,求取完成后会出现解得图像与原有图像灰度值上有差异,但所求图像成像均值细节效果好。这个差异本人目前采用按照灰度平均值差异进行加减。
上述方法即可解决大部分成像设备差异性带来的图像特征影响。
进而下一步即是如何在图像中找去最适合一致性校正的特征内容。
识别特征的方法本人所学过的,大致如下:
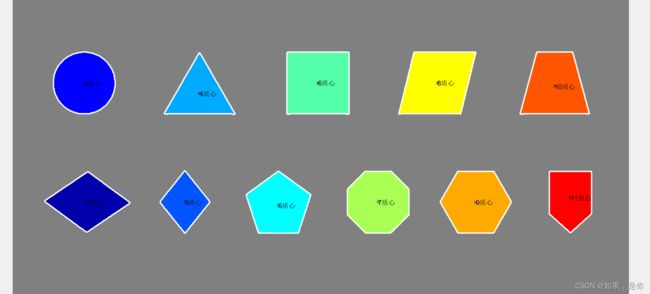
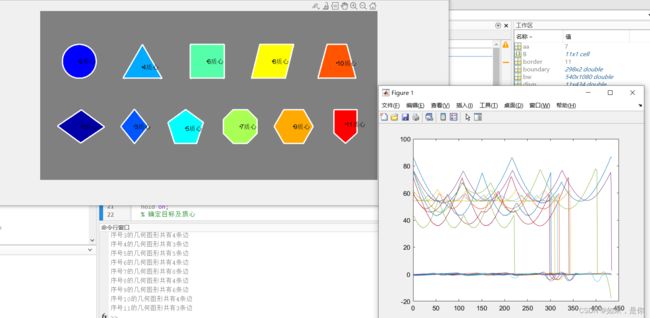
1.形状类型的定位,通过角点,圆周等几何形状特征进行特征几何属性的定位。(下图来源于网络,如侵权,请联系作者)
如上图(图像源于网络),图中共计11种常规几何形状。识别不同几何形状,本人采用了基于质心到边缘的 距离拟合方法。任举其中几种几何形状,运行结果如下:
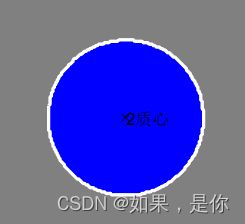
如上图,通过边缘范围到质心的距离,在上述距离中,通过斜率关系可以直接测试出所求取特征几何图形边的数量,即使上图标序号2的圆形,放大发现也是边数较多的几何图形。
在完成距离曲线的求取后,进一步,如何对曲线中的边数进行自动识别:由于
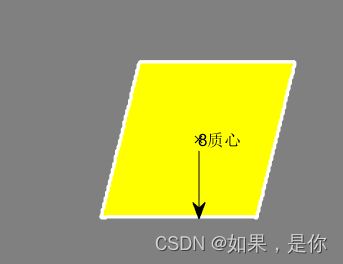
上图所示箭头点,类似于这种点,在距离曲线上也呈现出斜率为零的情况,亦或是下图:
在到达箭头所指点时,斜率的变化可能为零,可能为增,可能为减,斜率受到两侧边长比的影响,可能出现各类情况。所以直接使用斜率对多边形边数计算难以实现。
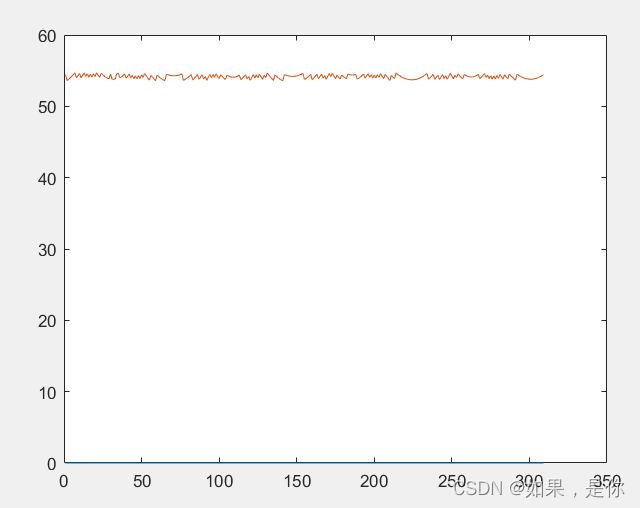
本人采用一种质心到边长的动态变化方法,即先对几何图形求取质心,然后依次计算边缘集合到质心的距离。如下图结果:
上图为识别几何图形,其边缘各点到质心的距离如下图蓝线:下图红线则是对蓝线所述距离的求导过程,通过红线经过0的次数,并处以2,即可得到上述几何图形的边长。
综合测试结果如下图:
该方法在大多几何图形内容中,均可以正确识别,例如对上图中,圆形的识别为12条边,本人设定阈值大于10即可认为是圆形。
上述方法的源码如下:
clear;clc;close all
%%
%% 几何形状识别
img1=imread('1.jpg');%输入想要识别的图像
threshhold =graythresh(img1);
bw=im2bw(img1,threshhold);
bw=1-bw;
%圆形
% se = strel('rectangle',[8,8]);
% bw = imclose(bw,se);
bw = imfill(bw,'holes');
[B,L] = bwboundaries(bw,'noholes');
figure(2);imshow(label2rgb(L,@jet,[.5 .5 .5]));
hold on;
% border=length(B);
border=length(B);
for k = 1:border
boundary = B{k};
plot(boundary(:,2),boundary(:,1),'w','LineWidth',2)
end
hold on;
% 确定目标及质心
stats = regionprops(L,'Area','Centroid');
% 设置求面积
for k =1:border
boundary = B{k};
mm(k,:)=stats(k).Centroid;
mn=B{k};
mn(:,[1 2])=mn(:,[2 1]);
[long(k),wide]=size(mn);
for j=1:long(k)
dism(k,j)=norm(mm(k,:)-mn(j,:));
end
hold on
plot(mm(k,1),mm(k,2),'k.'),text(mm(k,1),mm(k,2),[num2str(k),'质心']);
end
figure()
for i=1:border
aa=1;
plot(smooth(dism(i,:),0.01,'loess'));
hold on
% plot(diff(dism(i,:)));
fdism(i,:)=diff(dism(i,:));
fdism(i,:)=smooth(fdism(i,:),0.1,'loess');
plot(fdism(i,:));
for j=1:long(i)-2
if (fdism(i,j)<0&&fdism(i,j+1)>=0)||(fdism(i,j)>0&&fdism(i,j+1)<=0)
aa=aa+1;
end
end
if floor(aa/2)>1
disp(['序号',num2str(i),'的几何图形共有',num2str(floor(aa/2)),'条边'])
end
end但上图结果中的图形11识别明显错误。这是由于质心到边缘的距离在经过钝角边角时,距离的倒数可能为单向倒数,所以仅经过了1次0,故而除以二后,11图形将下面两边与上面右边或左边的某一边识别为一边,出现问题。要想解决这个问题,主要方法分为角点及角度识别,几何斜率判定及图像面积与边长关系细分实现。
角点角度识别,首先需要对图像中的角点进行提取并识别,识别完成焦点后,对角点侧边进行斜率判断,并通过斜率解算角度求解,这个过程有亿点点麻烦,并且基于这个过程,基本可以直接识别几何图形的边数。这个过程的难点在于对角点的识别,通过二值化可以直接得到边缘和区域,但角点的识别,往往需要图像本身有较高的素质,对于模糊的图像,或者分辨率低的图像,角点难以有效识别。
几何斜率判定和图像面积与边长的关系,这个具体的过程,就是通过目前的参数,可以得到图像的面积,同时可以得到整体图像周长,那么无论是任何图形,在识别过程中一定可以得到一条已知边。其次,通过浅显易懂的数学过程可知,相同面积条件下,边长越多,周长越小。所以在边长与周长及面积存在一定的相关关系。
具体分析,可列举出以下特殊情况作为临界点。
确定边数和周长,将周长平均分配,即可得到能够封闭构成几何面积的最大值。
确定面积和边数,可得到理想最小周长。
确定面积和周长,可得到理想最小边数。
根据三者间的关系进行判断,确定类别后进一步进行特征求解。
2.二值化分布,提取按照灰度属性的特征内容。
3.本人在实际处理时,难免遇到上述两种提取方法难以有效提取的内容,一般是形状杂乱,灰度边缘模糊的内容,本人一般进行生长-腐蚀-生长-腐蚀....,和对比度拉伸,边缘提取。完成步骤后,重新按照提取的边缘依照灰度值在原有图像上进行校准。