cs224w 图神经网络 学习笔记(三)Motifs and Structural Roles in Networks
课程链接:CS224W: Machine Learning with Graphs
课程视频:【课程】斯坦福 CS224W: 图机器学习 (2019 秋 | 英字)
这一课主要是讲 子图(subnetworks) 的一些参数。
目录
-
- 1. 序:子图(Subnetworks)
- 2. Subgraphs, Motifs and Graphlets
-
- 2.1 Network Motifs
- 2.2 Graphlets: Node feature vectors
- 2.3 Finding Motifs and Graphlets
- 3. Structural Role in Networks
-
- 3.1 Role的定义
- 3.2 Discovering Structural Role in Networks
1. 序:子图(Subnetworks)
子图(subnetworks/subgraph)是网络的局部组成,可以用来辨别和区分网络。(类似于分子中的不同原子结构)
子图的结构可以有很多种,比如有向图的三节点子图(n-node subgraphs,这里n=3)就有如下几种形式:

对于一张网络来说,你可以得到很多个子图,那么什么样的子图是有意义的呢?这就需要一些参数,来衡量子图的重要性。这样,不同的网络就可以表示为以这些子图为基的特征向量。

下面是一些例子:

我们首先看这张图最底下,横坐标,是前面讲到的13种子图的类型,上面的每一行就是不同网络关于这13种子图的一些特征值。可以看到,同领域的网络,它的特征向量其实是相似的。比如最后一行的语言网络,对于英语、发育、西班牙语、日语等不同的语言来说,他们尽管语法不尽相同、词语不同,但是它们的特征是一致的。
那么,我们今天的课程内容就是来看一下怎么去定义这样的“motifs”(可以理解为以子图构成的基底),怎么去得到网络关于这些基的特征值。
2. Subgraphs, Motifs and Graphlets
2.1 Network Motifs
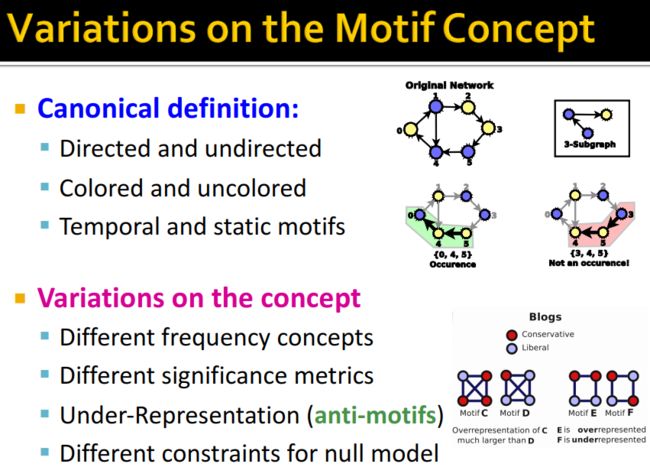
首先,我们先来看一下Network Motifs的定义:
“recurring, significant patterns of interconnections”
Motifs的作用:
- Help us understand how networks work(帮助我们了解网络是如何工作的)
- Help us predict operation and reaction of the network in a given situation (帮助我们预测网络在特定情况下的运行和反应)
Motifs的一些例子:
| Motifs | 图例 | 出现的网络 |
|---|---|---|
| Feed-forward loops 前馈环路 | 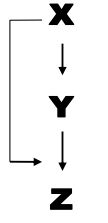 |
这种Motifs会在神经元网络中出现,会用来中和“生物噪音(biological noise)”。(这应该是属于生物信息学中的相关概念) |
| Parallel loops 平行环路 | 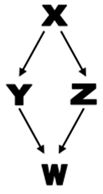 |
会在食物链网络中出现 |
| Single-input modules | 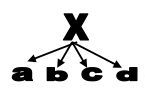 |
在基因控制网络中发现 |
这里有三个关键词:
- Pattern:motifs的模式是小的诱导子图(small induced subgraph。这里需要厘清诱导子图的定义(子图、诱导子图和生成子图)
- recurring:需要在网络中重复很多次;并且重复的Motifs里会有相同的单元(节点)。
- significant:比想象中出现得更加频繁。这里可以由一个关键点来衡量——Subgraphs that occur in a real network much more often than in a random network have functional significance(也就是说,定义的motifs在真实网络中出现的频率要比在随机图中出现的频率要高得多)。【可以看这篇文章:在论文中经常读到的motifs是什么意思?】这里需要注意的是用来做检测的随机网络需要和真实网络有相同的 #(nodes), #(edges), #(degree distribution),#表示数目。
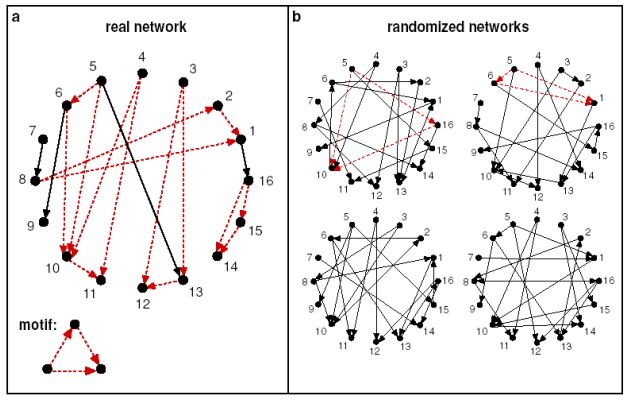
我们怎样去计算这个significance(显著性)呢?设 Z i Z_i Zi表示motif i i i的统计显著性。
Z i = ( N i r e a l − N ‾ i r a n d ) / s t d ( N i r a n d ) Z_i=(N{^{real}_i}-\overline{N}{^{rand}_i})/std(N{^{rand}_i}) Zi=(Nireal−Nirand)/std(Nirand)
这里 N i r e a l N{^{real}_i} Nireal是指在真实网络 G r e a l G^{real} Greal中motif i i i出现的次数, N i r a n d N{^{rand}_i} Nirand是指在随机网络 G r a n d G^{rand} Grand中motif i i i出现的次数。
那么,网络的motif i i i的显著性(Network Significance Profile, S P SP SP)由标准化后的 Z i Z_i Zi表示:
S P i = Z i / ∑ j Z j 2 SP_i=Z_i/\sqrt{\sum_j Z{^2_j}} SPi=Zi/j∑Zj2
S P SP SP更强调不同子图之间的相对显著性,这对于不同规模的网络比较十分有意义,因为一般来说网络规模越大,Z-score越高,而标准化处理则可以降低尺度效应的影响。
这里有个问题,就是我们怎么得到随机网络 G r a n d G^{rand} Grand呢(Configuration model)?并且这个随机网络 G r a n d G^{rand} Grand需要和真实网络有相同的 #(nodes), #(edges), #(degree distribution)。
这里介绍两种方式。
第一种方式,我们可以通过给定的节点数量和节点的度序列(degree sequence k 1 , k 2 , ⋯ , k N k_1,k_2,\cdots,k_N k1,k2,⋯,kN)来生成随机图:
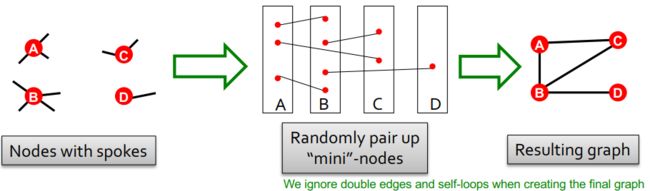
注意,这里为了保留随机性,不会遍历所有的搭配可能;并且可以看到,因为我们会忽略自环和双边,最后生成的随机图中节点B的度为3(给定的度为4)。
第二种方式称为Switching。

我们从一个给定的图开始(这个图和真实的网络有相同的度),重复以下步骤 Q ⋅ ∣ E ∣ Q \cdot |E| Q⋅∣E∣次, Q Q Q会取一个较大的值(如100)来使整个过程达到收敛:
- 随机选取一条边(例如A->B,C->D)
- 将边的终点随机改变。注意的是新生成的边不能构成自环或者双边。
2.2 Graphlets: Node feature vectors
Graphlets(图元,connected non-isomorphic subgraphs)是指大规模网络中那些节点数目较少的连通诱导子图。
Graphlets反映了网络的局部拓扑,所以它是重要的网络特征。
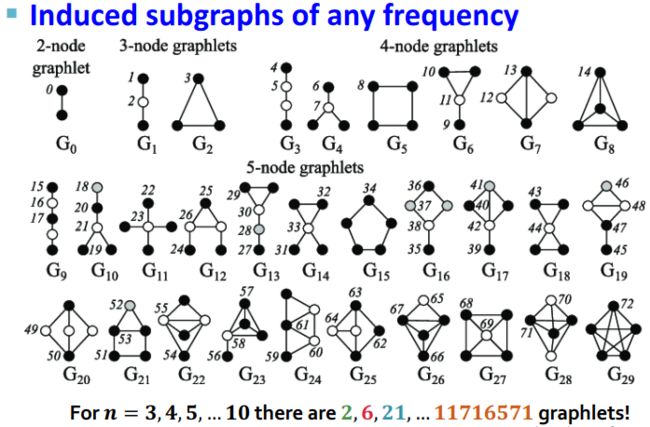
图元通常会用来比较网络之间的相似和差异。基于图元,我们来介绍Graphlet Degree Vector(GDV) 方法。
Graphlet Degree Vector(GDV)方法是Przulj在2003年提出的利用图元及图元向量来刻画网络中节点邻域关系的方法,具体指在小连通非同构子图中计算每个节点的自同构轨道,即每个节点所接触的图形数量。这种方法基于网络拓扑和邻域定义了一系列非同构子图和图向量,用于识别网络中结构相似的模块。
——宋祥帅, 杨伏长, 谢江,等. Graphlet Degree Vector方法的优化与并行[J]. 计算机应用, 2020, 40(2):398-403.


Graphlet Degree Vector(GDV)是一个向量,表示每个轨道位置具有该节点的频率。它刻画的是每个节点接触的图元数量。
我们看下面这个例子:
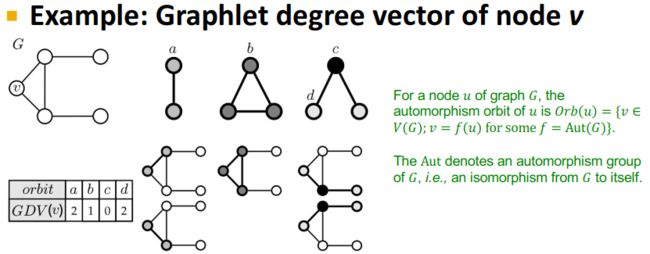
我们有三种不同的轨道(orbit),轨道上有a、b、c、d四种节点位置(orbit position)。对于节点 v v v来说,其在轨道位置a上有2个图元,在轨道位置b上有1个图元,在轨道位置c上没有图元,在轨道位置d上有2个图元。这里需要注意的是图元是诱导子图。
因此,Graphlet Degree Vector(GDV)的实际意义在于:
- Graphlet degree vector counts #(graphlets) that a node touches at a particular orbit. 刻画了某个节点所接触的图元(某个特殊的轨道位置的图元)的数量。
- Graphlet degree vector provides a measure of a node’s local network topology. 刻画了网络中节点的局部属性。
2.3 Finding Motifs and Graphlets
第一步,找到所有的子图:Counting Subgraphs——Exact subgraph enumeration (ESU)算法
ESU算法中有两个重要的集合:
V s u b g r a p h V_{subgraph} Vsubgraph——表示当前创建的子图(motif)。
V e x t e n s i o n V_{extension} Vextension——表示可以用来扩展motif的节点集合。
ESU的基本思想是:从一个节点 v v v出发,从 V e x t e n s i o n V_{extension} Vextension中添加满足下面两个条件的节点 u u u——①节点 u u u的编号要大于节点 v v v的编号;②节点 u u u可以是当前新增点 w w w的邻居节点,但不能是已经在 V s u b g r a p h V_{subgraph} Vsubgraph集中的节点的邻居节点。
ESU算法是通过递归实现的,算法的过程可以看成是深为 k k k的递归树——ESU树。
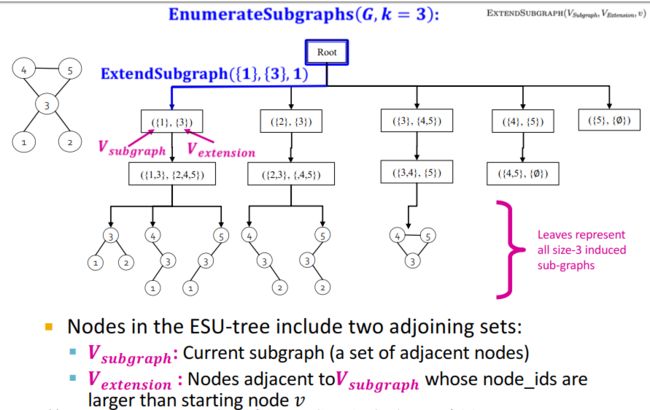
第二步:对找到的子图进行统计:Count the graphs
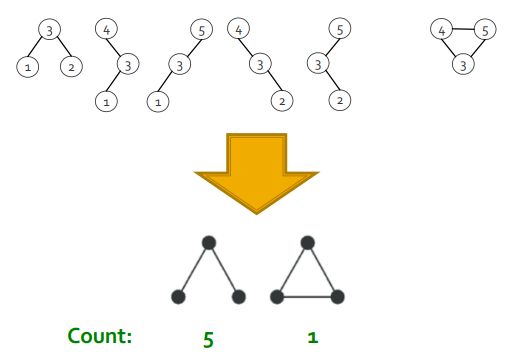

将ESU树叶子节点上的子图分成k阶不同构的各种类别。这里涉及到怎么判断图之间是否同构,采用的是McKay的方法。
3. Structural Role in Networks
3.1 Role的定义
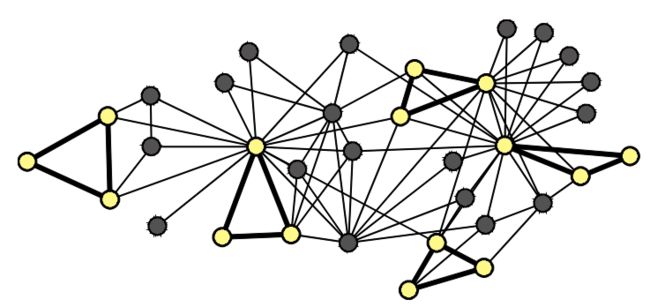
Roles are “functions” of nodes in a network
区别Role和Group/Communities:
- role是指在网络中具有相似功能的节点:例如不同项目组中的研究员,这些研究员在网络中可能并没有连接(互不认识),但他们从事同样的一份工作。即role取决于相似性而不是相互连接性。
- group/community则是互相连接的个体(节点),核心在于连接性。

我们来给role一个更严谨的定义。属于相同role的节点具有结构等价性(structural equivalence)——Nodes u u u and v v v are structurally equivalent if they have the same relationships to all other nodes.
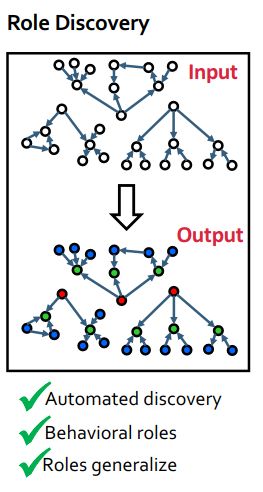
3.2 Discovering Structural Role in Networks
Why are Roles important?

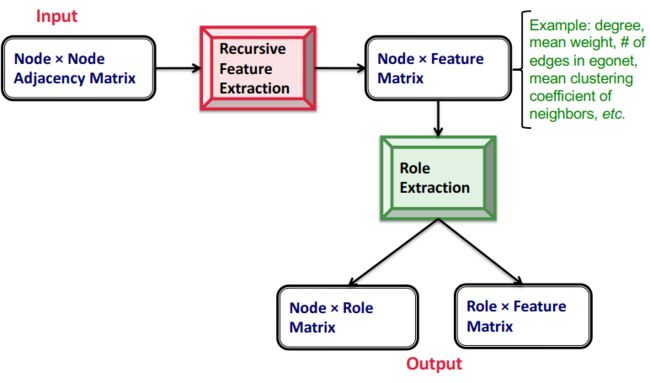
方法:RoIX——Automatic discovery of nodes’ structural roles in networks [Henderson, et al. 2011b]
该方法的特点:
- Unsupervised learning approach 无监督学习方法
- No prior knowledge required 不需要任何先验知识
- Assigns a mixed-membership of roles to each node 为每个节点分配角色的混合成员关系
- Scales linearly in #(edges) 算法的复杂度随着网络中的边的数量线性增长