李宏毅 || 机器学习笔记一

李宏毅 || 机器学习笔记一

这是李宏毅老师的2021春季机器学习课程笔记。现在开始第一节 Introduction 的学习

首先简单介绍一下机器学习

1.什么是机器学习呢？

事实上，机器学习概括来说可以用一句话来描述机器学习这件事，机器学习就是让机器具备找一个函式的能力

2.机器学习三大任务

• Regression，回归问题，输出是一个连续的数值、标量，比如PM2.5预测。
• Classification，分类问题（输出为离散数值），二分类（Binary Classification）的输出就是0或1、Yes或No。多分类（Multi-Category Classification）的输出就是[1,2,3,…,N]，比如图像分类里判断一张图片是猫还是狗还是杯子。
• Structured learning，结构学习（输出为一个有结构的内容，如一张图画、一段文字）

3.机器学习步骤

Function with unknown parameters(写出一个带有未知参数的函数)
（Ex. Linear Model y=wx+b. 这里y即是一个model，w、b为待训练的参数）

Define loss fun from training data(定义loss函数)

Optimization(优化的方法为Gradient decent)

举例

机器学习找这个函式的过程，分成三个步骤，那我们就用Youtube频道，点阅人数预测这件事情，来跟大家说明这三个步骤，是怎么运作的。

Step 1. Function with Unknown Parameters

第一个步骤是我们要写出一个，带有未知参数的函式，举例来说，我们这边先做一个最初步的猜测，我们写成这个样子 y=b+w*xₗ 这边的每一个数值是什么呢。

• y是我们准备要预测的东西，我们准备要预测的是今天（2月26号）这个频道总共观看的人；
• xₗ是这个频道前一天总共观看的人数，y跟xₗ都是数值，叫做特征（Feature）；
• **b（**Bias)跟w（weight）是未知的参数（Parameter），它是准备要通过资料去找出来的，我们还不知道w跟b应该是多少，我们只是隐约的猜测；

这个猜测往往就来自于，你对这个问题本质上的了解，也就是Domain knowledge，这是一个猜测，它不一定是对的，之后会再来修正这个猜测。

Step 2. Define Loss from Training Data

定义Loss Function，这个Function的输入是Parameter，即Model里面的参数b跟w；输出的值代表这笔数值好还是不好。那这个Loss怎么计算呢？

函式预估的结果跟真正的结果（这个真实的值叫做Label）的差距有多大。估测的值用y来表示，真实的值用ŷ来表示，计算y跟ŷ之间的差距eₗ、

计算差距其实不只一种方式

• 算y跟ŷ之间，绝对值的差距，这一种计算差距的方法，得到的这个大L，得到的Loss叫 mean absolute error（MAE）
• 如果e是用相减y平方算出来的，这个叫mean square error（MSE）
• 如果y和ŷ它都是机率分布的话，可能会选择Cross-entropy

接下来我们把每一天的误差加起来然后取得平均，N代表训验资料的个数，算出一个L，是每一笔训练资料的误差，就是Loss。L越大，代表现在这一组参数越不好，L越小，代表现在这一组参数越好。

估测的值跟实际的值之间的差距。

Error Surface：

对所计算出来的结果，那我们可以调整不同的w，我们可以调整不同的b，组合起来以后，都去计算它的Loss，然后就可以画出下面的这个等高线图。

如上图所示，越偏红色系，代表计算出来的Loss越大，就代表这一组w跟b越差，如果越偏蓝色系，就代表Loss越小，就代表这一组w跟b越好。那像这样子的一个等高线图，就是试着试了不同的参数，然后计算它的Loss，画出来的这个等高线图，叫做Error Surface，那这个是机器学习的第二步。

Step 3. Optimization

解一个最佳化的问题。把未知的参数w跟b，找一个数值出来，代入L，让Loss的值最小，那个就是我们要找的w跟b。

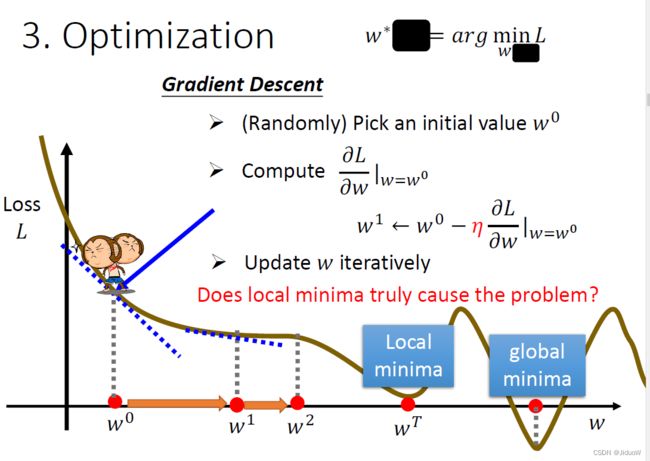
在这一门课里面唯一会用到的Optimization的方法，叫做梯度下降法（Gradient Descent）。先假设未知的参数只有一个，只有w这个未知的参数。

那当w代不同的数值的时候，就会得到不同的Loss，这一条曲线就是error surface

那怎么样找一个w，去让这个loss的值最小呢?

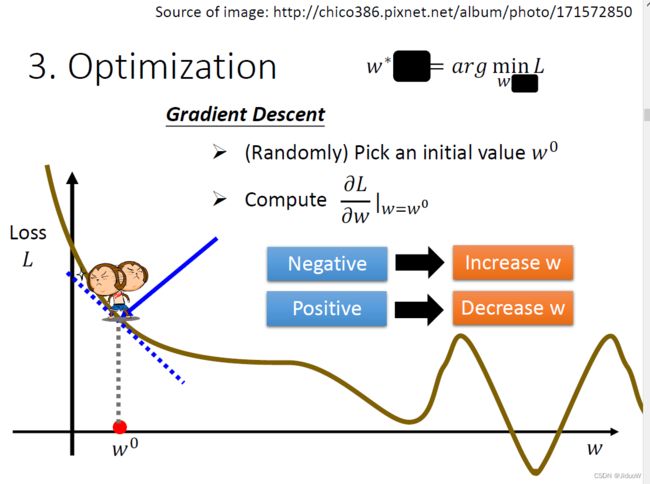
首先随机选取一个初始的点w₀，
那接下来你就要计算，在w等于w0的时候，w这个参数对loss的微分L/∂w |(w=w^0 )，计算在w₀这个位置的error surface的切线斜率。
这一步的步伐的大小取决于两件事情：

• 第一件事情是这个地方的斜率有多大，这个地方的斜率大，这个步伐就跨大一点，斜率小步伐就跨小一点。
• 另外一个东西会影响步伐大小，这个η叫做学习速率（learning rate），它是你自己设定的。如果η设大一点，那你每次参数update就会量大。

这种你在做机器学习需要自己设定的东西叫做hyperparameters。

为什么loss可以是负的呢?

Loss这个函数是自己定义的，决定一个loss function，就是绝对值再减100，那你可能就有负的，所以我这边这一个curve并不是一个真实的loss，

那我们说我们要把w⁰往右移一步，那这个新的位置就叫做w¹，然后再继续反覆做同样的操作，不断的把w移动位置，最后你会停下来。

什么时候会停下来呢?往往有两种状况：

• 第一种状况开始的设定，最多计算几次。
• 那还有另外一种理想上的，微分的值正好是0的时候，如果这一项正好算出来是0，0乘上learning rate η还是0，

Gradient Descent 这个方法，有一个巨大的问题，在这个例子里面，从W^{0当作随机初始的位置，很有可能走到W}T这里，你的训练就停住了，你就没有办法再移动w的位置。那右侧红点这一个位置，这个真的可以让loss最小的地方，叫做全局最小值（global minima），而W^T这个地方叫做局部最小值（local minima）

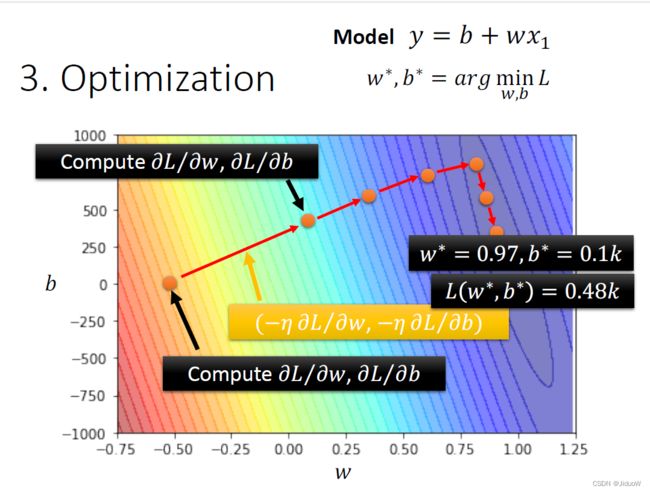
那有两个参数的情况下，怎么用Gradient Descent呢？

我们现在有两个参数，都给它随机的初始的值，就是w⁰跟b⁰
你要计算w跟loss的微分和b对loss的微分，计算是在w等于w⁰的位置，b等于b₀的位置，你要计算w对L的微分，计算b对L的微分，
计算完以后，就根据之前一个参数的时候的做法去更新w跟b，把w⁰减掉learning rate乘上微分的结果得到w¹，把b⁰减掉learning rate乘上微分的结果得到b¹

Linear Model

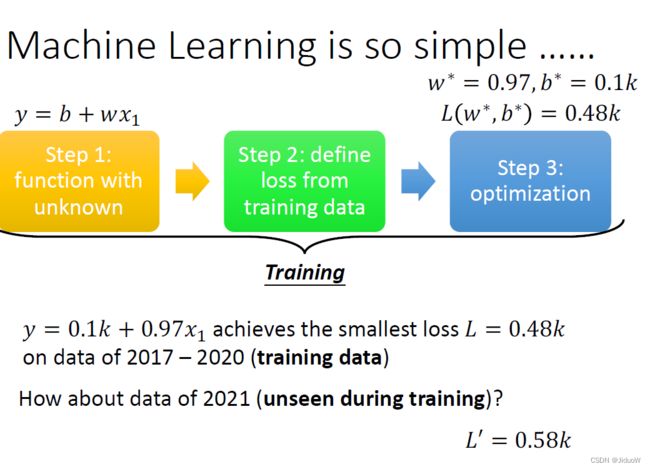
这三个步骤合起来叫做训练。我们现在是在知道答案的资料上去计算loss。

但是我们真正要在意的是未来的观看的次数是多少，所以接下来拿这个函式来真的预测一下未来的观看次数。

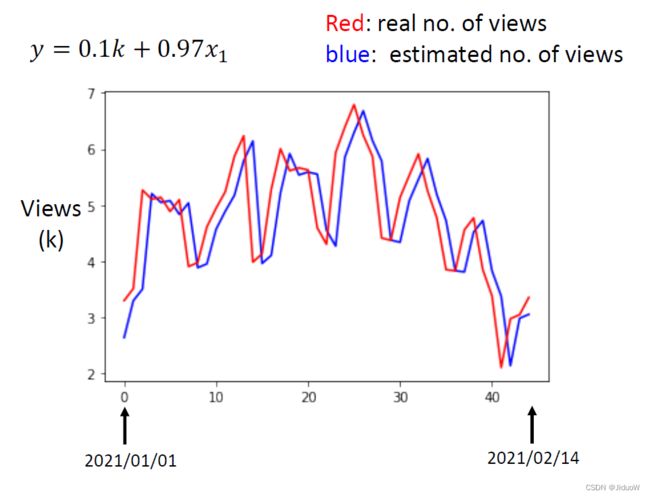
能不能够做得更好呢，在做得更好之前，我们先来分析一下结果：

• 横轴是代表的是时间，所以0（最左边的点），代表的是2021年1月1号，最右边点代表的是2021年2月14号
• 纵轴就是观看的人次，这边是用千人当作单位；
• 红色的线是真实的观看人次
• 蓝色的线是机器用这一个函式，预测出来的观看人次

这蓝色的线没什么神奇的地方，因为我们觉得，可以拿前一天的观看人次去预测隔天的观看人次。但是仔细观察这个图，它是有周期性的，它每隔七天就会有两天特别低，所以既然我们已经知道每隔七天是一个循环，那这一个model显然很烂，因为它只能够看前一天。

每隔七天它一个循环，如果我们一个模型，它是参考前七天的资料，把七天前的资料，直接复制到拿来当作预测的结果，也许预测的会更准也说不定，所以我们就要修改一下我们的模型。通常一个模型的修改，往往来自于你对这个问题的理解，就是Domain Knowledge。

所以一开始，我们对问题完全不理解的时候，我们就胡乱写一个 y=b+wx_1 ，效果并没有特别好。接下来我们观察了真实的数据以后，得到一个结论是，每隔七天有一个循环，所以我们应该要把，前七天的观看人次都列入考虑，所以写了一个新的模型。

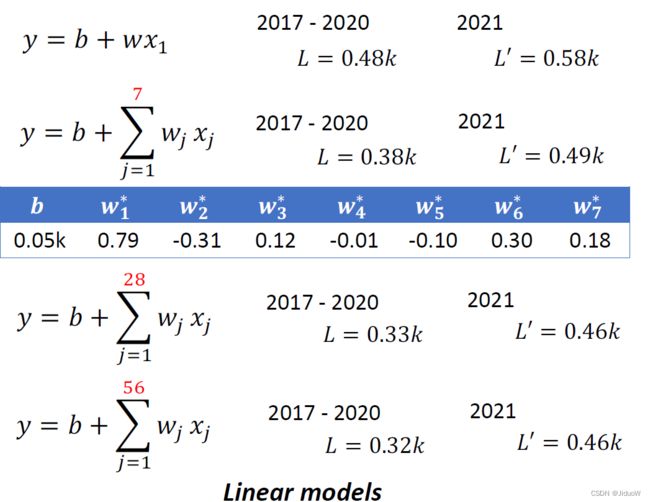
xⱼ的下标j代表是几天前，然后这个j等于1到7，那七天前的资料，乘上不同的weight，再加上bias，得到预测的结果。如果这个是我们的model，

那这边每一个w跟b，我们都会用Gradient Descent，算出它的最佳值，它的最佳值长什么样子呢，这边show出来。

本来是考虑前七天，然后考虑28天会怎么样呢，28天就一个月，考虑前一个月每一天的观看人次，去预测隔天的观看人次，预测出来结果怎样呢，训练资料上是0.33k，那在2021年的资料上，在没有看过的资料上是0.46k，那接下来考虑56天会怎么样呢？是0.32k，在没看过的资料上还是0.46k，看起来，考虑更多天没有办法再更进步了，也许已经到了一个极限。

这边这些模型输入x（feature），把feature乘上一个weight，再加上一个bias就得到预测的结果，这样的模型有一个共同的名字，叫做Linear model，那我们接下来会看，怎么把Linear model做得更好。

Regression

1.拟合一条分段折线

Piecewise Linear Curves

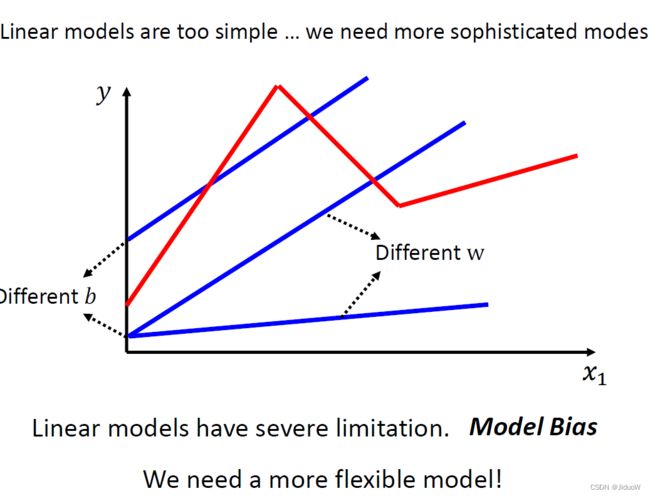
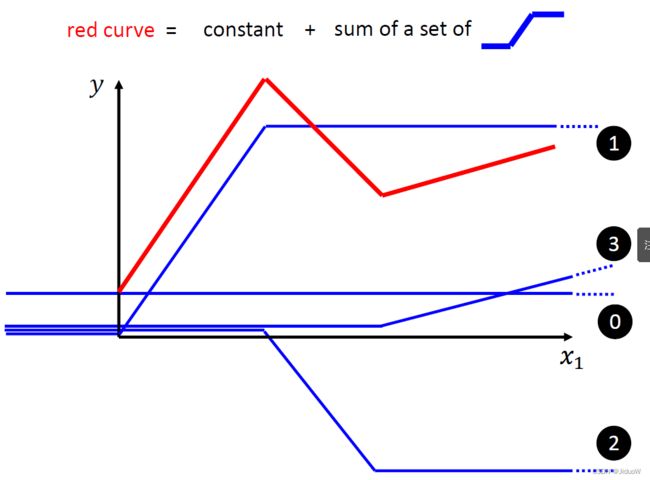
对于下面这条红线（piecewise linear curve），你永远不能用Linear Model来很好的拟合它。所以我们需要一个更加有弹性的，有未知参数的Function。

如上图，仔细观察红色的这一条曲线，它可以看作是一个常数，再加上一群蓝色的这样子的 Function。事实上，

• 任何piecewise linear curve（分段线性线段）都可以看作是一个常数，再加上一堆蓝色的Function。
• 任何连续曲线，你只要取足够多的转折点，你都能用piecewise linear curve去逼近他
• 为什么不用分段函数呢，因为在断点处，分段函数不可以求导

如果你今天点取的够多或取的位置适当的话，这个 Piecewise Linear 的 Curves，就可以逼近这一个连续的这一个曲线。

2.怎么表示这个蓝色折线呢？

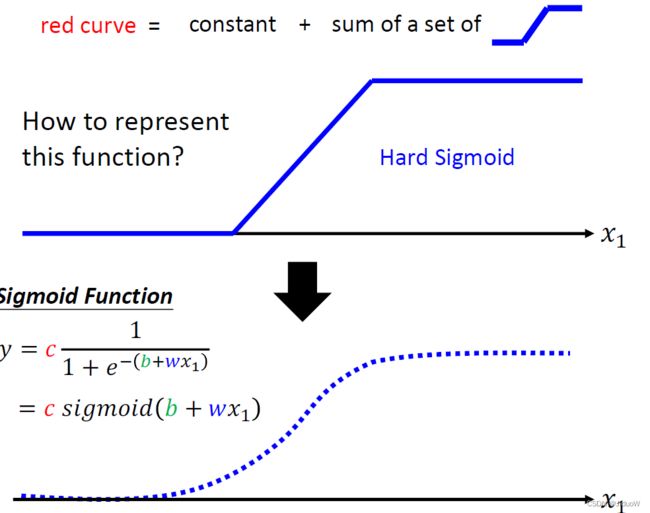
那么如何来表示这个蓝色的折线呢（即Hard Sigmoid）？这里用了Sigmoid函数，它可以逼近Hard Sigmoid。

Back to ML_Step 1 :function with unknown

用一条曲线来理解它，用一个Sigmoid 的 Function来逼近这个蓝色的Function，Sigmoid Function表达式为：

输入的 x1，我们先乘上一个 w，再加上一个b，再取一个负号，再取 Exponential，再加 1，这一串被放在分母的地方。当然，前面可以乘上一个 Constant 叫做 c。

如果输入的这个 x1 的值，趋近于无穷大的时候，那 e^{-(b+wx_1)}这一项就会消失，那当 x1 非常大的时候，这一条这边就会收敛在这个高度是 c 的地方。
那如果 x1 负的非常大的时候，分母的地方就会非常大，那 y 的值就会趋近于 0。

如上图所示，我们再回到这个蓝色的 Function，比较常见的名字就叫做Hard Sigmoid。我们要组出各种不同的曲线，就需要各式各样合适的蓝色的 Function，而这个合适的蓝色的 Function 怎么制造出来呢？

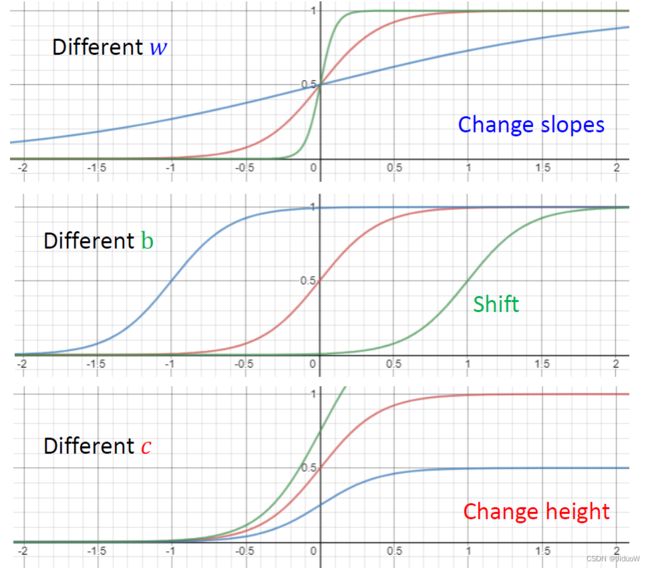
如上图所示，修改不同的参数会得到不同的效果：

如果你改 w ，会改变斜率（斜坡的坡度）
如果你改 b ，Sigmoid Function 可以左右移动
如果你改 c ，可以改变它的高度（曲线和y轴的交点）
因此，你只要有不同的 w 、b 和 c，你就可以制造出不同的Sigmoid Function，把不同的 Sigmoid Function 叠起来以后，你就可以去逼近各种不同的Piecewise Linear 的 Function，然后 Piecewise Linear 的 Function可以近似各种不同的 Continuous 的 Function。

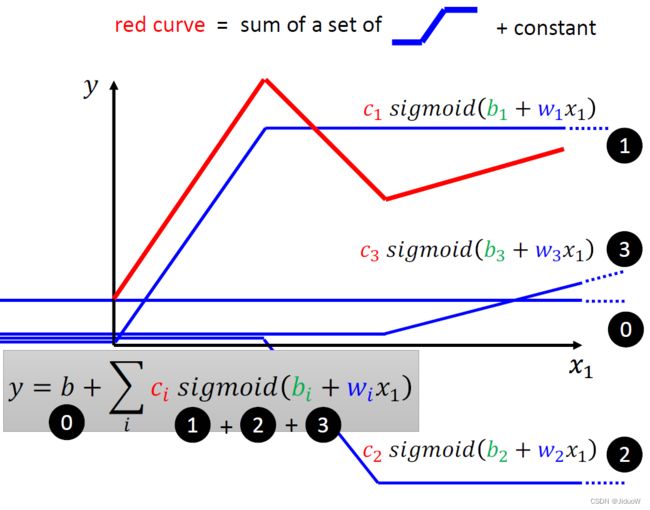
我们知道说红色这条线就是 0+1+2+3，它们都是蓝色的 Function，函式有一个固定的样子（b+wx_1），去做 Sigmoid 再乘上 c1。只是 1 跟 2 跟 3的 w 不一样，它们的 b 不一样，它们的c 不一样。如果是第一个蓝色 Function，它就是 w1、b1、c1，第二个蓝色 Function是 w2、b2、 c2，第三个蓝色 Function是 w3、b3、c3。加起来以后，我们得到的函式为 ：

这个 Function里面的 b 跟 w 跟 c是未知的，都是我们未知的参数。

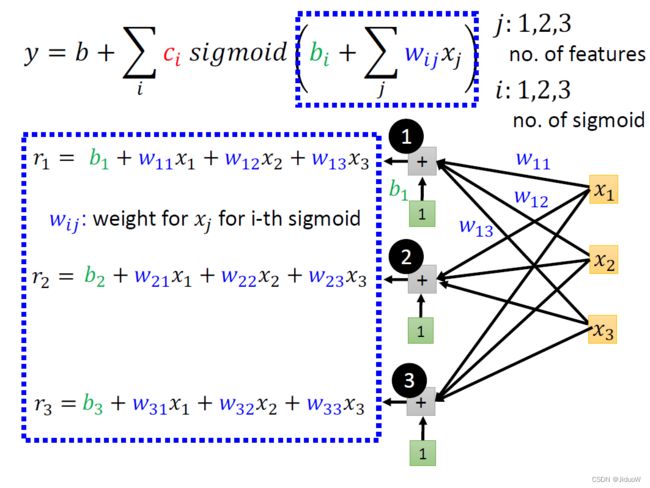
如上图，我们不是只用一个 Feature X_1，我们可以用多个 Feature。

• i来表示不同的sigmoid函数
• j来表示Feature的编号。

x1 ：前一天的观看人数，x2：两天前观看人数，x3：三天前的观看人数
每一个i 就代表了一个蓝色的 Function，只是我们现在每一个蓝色的 Function，都用一个 Sigmoid Function 来比近似它

我们现在为了简化起见，把括号里面的数字，用一个比较简单的符号r来表示。分别简记为： r1， r2，r3。可以表示为

如上图公式，把 x1 x2 x3 拼在一起变成一个向量，把这边所有的 w 统统放在一起变成一个矩阵，把 b1 b2 b3 拼起来变成一个向量，把 r1 r2 r3 拼起来变成一个向量。

如上图最后一行，最后简写成，向量 x 乘以矩阵W（9 个数值就是9 个 权重Weight），再加上 b 就得到 r 这个向量。那这边做的事情跟上边做的事情是一模一样的，只是表示的方式不一样。

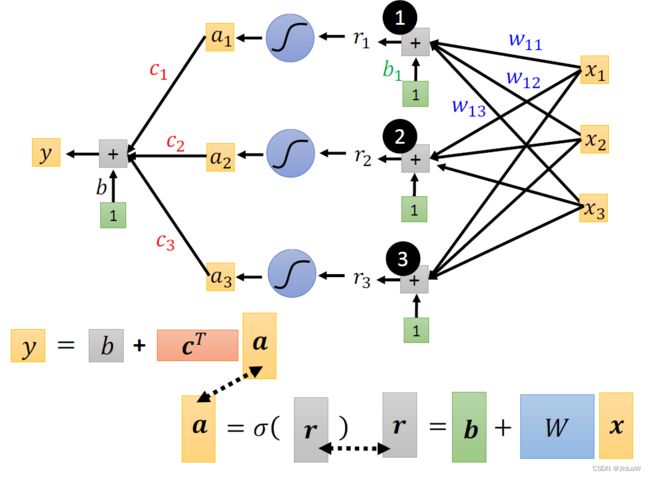
上面描述的是括号里的运算，把 x 乘上 W 加上 b 等于 r。那接下来 r 要分别通过 Sigmoid Function得到a。以r1为例：

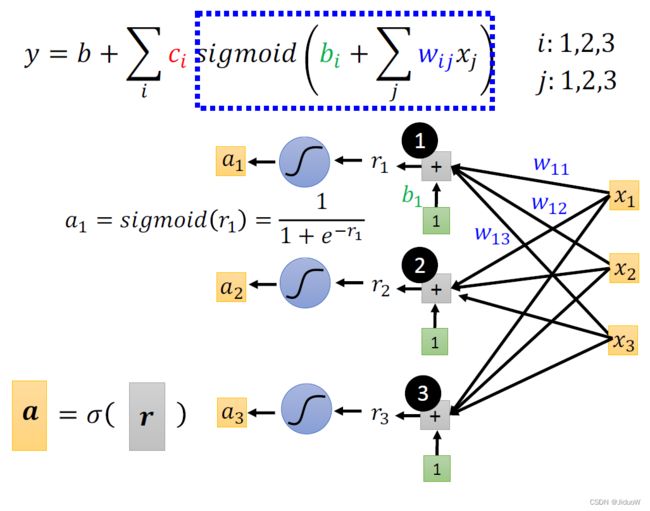
然后同样的方法由 r2 去得到 a2，把 r3 透过 Sigmoid Function 得到 a3。

因此，上图蓝色的虚线框完成了x到a。首先通过虚线框中的括号运算从 x1 x2 x3 得到了 r1 r2 r3。接下来通过Sigmoid Function，然后得到 a1 a2 a3。

接下来我们这个Sigmoid 的输出a，还要乘上 ci 然后还要再加上 b。用向量来表示的话，a1 a2 a3 拼起来叫这个向量 a，c1 c2 c3 拼起来叫一个向量 c（ 这里c 作 Transpose），那 a 乘上 c 的 Transpose 再加上 b，就得到了 y。

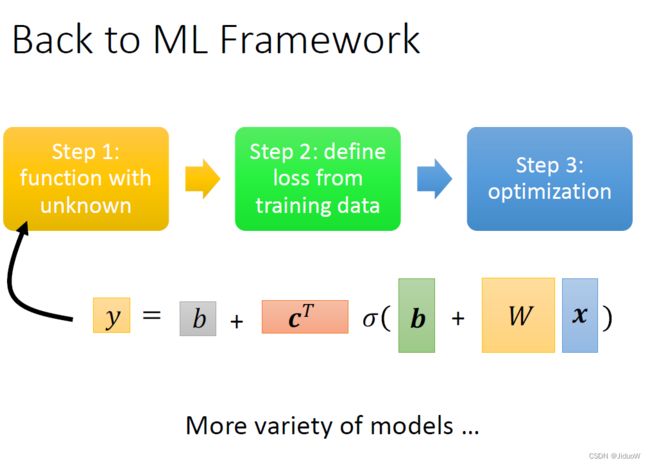
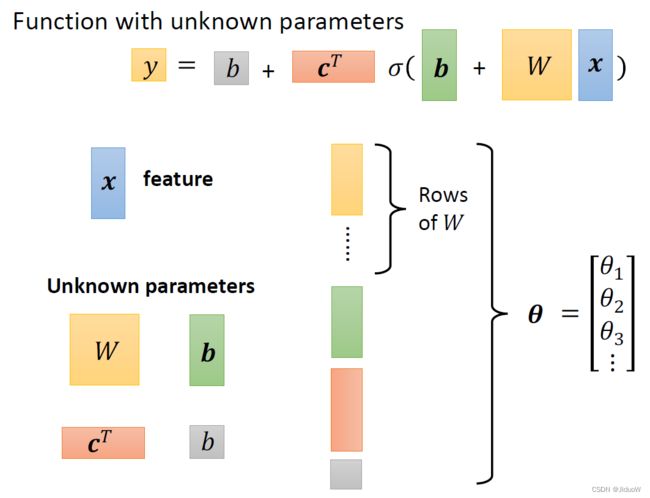
如上面公式，总结一下，它整体而言做的事情是输入Feature x 这个向量，x 乘上矩阵 w 加上向量 b 得到向量 r，向量 r 通过 Sigmoid Function得到向量 a，再把向量 a 跟乘上 c 的 Transpose 加上 b 就得到 y。

那我们把这些未知参数通通拉直，拼成一个很长的向量。用一个符号叫做 θ来表示它。θ是一个很长的向量，里面的第一个数值我们叫 θ1，第二个叫 θ2…，它统称我们所有的未知的参数。

Back to ML_Step 2 :define loss from training data

那接下来进入第二步：从训练数据定义loss函数。 Loss Function 变成 L( θ )。

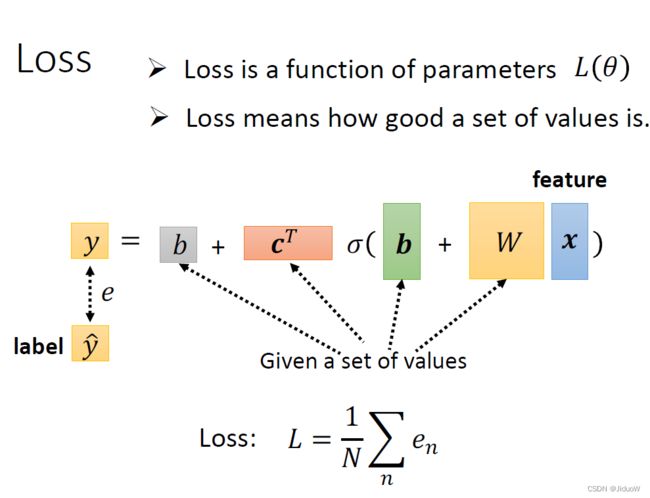
• 先给定某一组 W、b、c^T跟 b的初始值
• 然后把一种 Feature x 带进去，然后看看你估测出来的 y 是多少
• 再计算一下跟真实的 Label 之间的差距，你得到一个 e
• 把所有的误差通通加起来，你就得到你的 Loss

Back to ML_Step 3: Optimization

接下来下一步就是优化（Optimization），

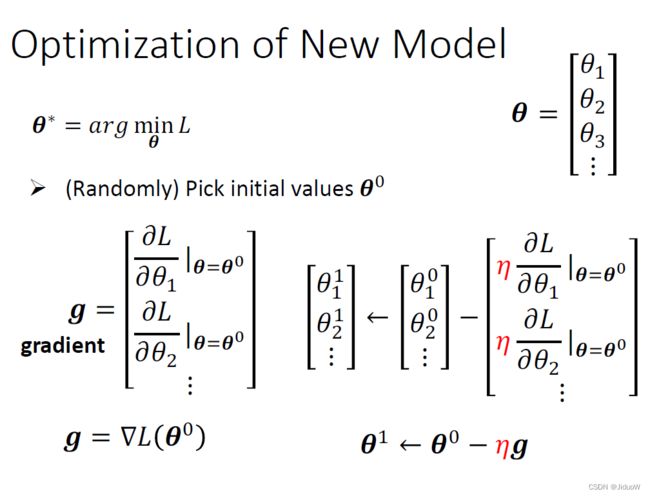
现在的 θ 它是一个很长的向量，要找一组 θ让我们的 Loss 越小越好，可以让 Loss 最小的那一组 θ，我们叫做 θ Star，θ^*，具体步骤如下：

（1）我们一开始要随机选一个初始的数值θ_0。
（2）接下来要计算微分，你要对每一个未知的参数，去计算对 L 的微分以后，集合起来它就是一个向量
（3）算出这个 g 以后，接下来呢我们Update参数。

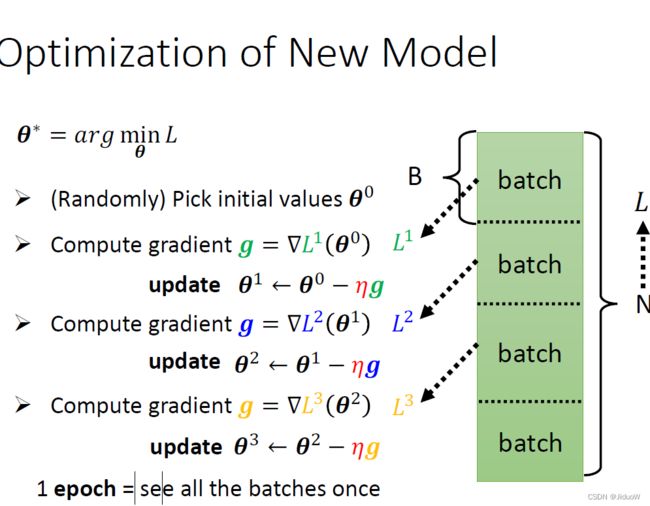
Batch

实际上在做 Gradient的时会这么做：会把这大 N 笔资料分成一个一个的 Batch（一包一包的东西，一组一组的），随机分就好，所以每个 Batch 里面有大B 笔资料，所以本来全部有大 N 笔资料，现在大B笔资料一组，一组叫做 Batch。

根据这个 L1 来算 Gradient，用这个 Gradient 来更新参数，接下来再选下一个 Batch 算出 L2，根据 L2 算出Gradient，叫做一个 Epoch，每一次更新参数叫做一次 Update， Update 跟 Epoch 是不一样的东西（每次更新一次参数叫做一次 Update，把所有的 Batch 都看过一遍，叫做一个 Epoch）。

全部batch叫做一个 Epoch，每一次更新参数叫做一次 Update， Update 跟 Epoch 是不一样的东西（每次更新一次参数叫做一次 Update，把所有的 Batch 都看过一遍，叫做一个 Epoch）。

补充：所谓 HyperParameter 就是你自己决定的东西，人所设的东西不是机器自己找出来的，叫做 HyperParameter，我们今天已经听到了，几个 Sigmoid 也是一个 HyperParameters，Batch Size 也是一个 HyperParameter。

模型变型

那我们其实还可以对模型做更多的变形.这个 Hard Sigmoid 不好吗，为什么我们一定要把它换成 Soft 的Sigmoid？

你确实可以不一定要换成 Soft 的 Sigmoid，有其他的做法。举例来说这个 Hard 的 Sigmoid，它可以看作是两个 Rectified Linear Unit 的加总，所谓 Rectified Linear Unit （ReLU）它就是长这个样。

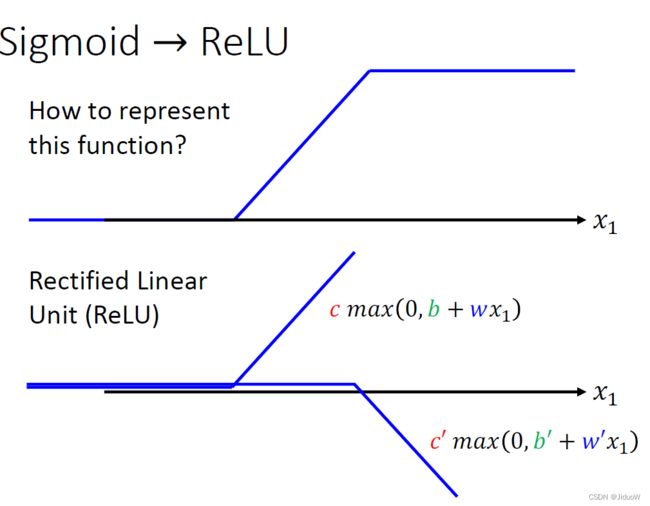
如上图，每条不同的 w 不同的 b 不同的 c，你就可以挪动它的位置，你就可以改变这条线的斜率，在机器学习里面，这条线我们叫做 Rectified Linear Unit，它的缩写叫做ReLU。

把两个 ReLU 叠起来就可以变成 Hard 的 Sigmoid。

那本来这边只有 i 个Sigmoid，你要 2 个ReLU，才能够合成一个 Hard Sigmoid ，所以这边有 i 个 Sigmoid，那如果ReLU 要做到一样的事情，那你可能需要 2 倍的 ReLU，所以我们把 Sigmoid 换成 ReLU。这边就是把一个式子换了，因为要表示一个 Hard 的 Sigmoid，表示那个蓝色的 Function 不是只有一种做法，你完全可以用其他的做法。那这个 Sigmoid或是 ReLU，他们在机器学习里面，我们就叫Activation Function。