Reinforced Neighborhood Selection Guided Multi-Relational Graph Neural Networks阅读笔记

Reinforced Neighborhood Selection Guided Multi-Relational Graph Neural Networks 阅读笔记

文章标题：Reinforced Neighborhood Selection Guided Multi-Relational Graph Neural Networks
文章链接：https://arxiv.org/pdf/2104.07886.pdf
代码链接：https://github.com/safe-graph/RioGNN
译者水平有限，如有纰漏，请阅读原文。

摘要

图神经网络（GNNs）已被广泛用于各种结构化图数据的表示学习，通常是通过不同操作聚合节点的邻域信息，在节点之间传递消息。尽管前景看好，但大多数现有GNN过分简化了图中边的复杂性和多样性，因此无法处理普遍存在的异构图（通常以多关系图表示形式）。在本文中，我们提出了一种新的强化、递归和灵活的邻域选择引导的多关系图神经网络结构RioGNN，它可以在保持关系依赖表示的同时导航神经网络结构的复杂性。我们首先根据实际任务构造一个多关系图，以反映节点、边、属性和标签的异构性。为了避免不同类型节点之间的嵌入过度同化，我们采用了一种基于节点属性的标签感知神经相似性度量来确定最相似的邻居。提出了一种增强的关系感知邻居选择机制，用于在聚合来自不同关系的所有邻居信息之前，选择关系中目标节点最相似的邻居，以获得最终的节点嵌入。特别是，为了提高邻域选择的效率，我们针对不同尺度的多关系图，提出了一种新的具有可估计深度和宽度的递归可扩展强化学习框架。RioGNN通过过滤阈值机制识别每个关系的个体重要性，可以学习更多区分性节点嵌入，并增强解释性。与其他比较GNN模型相比，真实世界图形数据和实际任务的综合实验证明了模型在有效性、效率和可解释性方面的进步。

1. 介绍

图形神经网络（GNNs）的发展使人们能够在多种领域进行有效的表征学习[103,118]，包括生物信息学、化学信息学、社会网络、自然语言处理[75,77]、社会事件[74,76]、推荐系统[80]、时空交通[28,78]、计算机视觉和物理[3]其中，图形是主要表示。GNN模型在不同的任务上，如节点分类[4,12,30,47,94]、节点聚类[40,53,72]、链接预测[46,50,113]、图分类，在大量数据集（引文网络[89,111]、生化网络[73,96,123]、社交网络[19]、知识图[57,83,105]等）上都达到了性能目标[18,73,90,109]等。GNN的核心是通过将节点特征传递给相邻节点来操作图结构上的各种聚合函数[30,47,94106]；每个节点聚合其邻居的特征向量以计算和更新其新特征向量。根据经验，聚合或消息传递的迭代进入节点嵌入向量——节点多跳邻域内结构信息和属性信息的数字捕获——由标签传播机制授权[27、56、71、81、122]。

异构图在真实世界系统中普遍存在；图通常由具有多种类型的节点和节点之间的多关系边组成。例如，在Yelp垃圾邮件评论数据[82]中，存在异构节点（例如，业务、评论、用户等）和关系（例如，由同一用户发布，在同一产品下具有相同的星级，在两次评论之间的同一月份发布的同一产品下）。然而，现有的GNN迭代聚合机制还没有仔细考虑语义关系的多样性和所提出的模型的可用性。同质GNN，如GraphSAGE[30]、GCN[47]、GAT[94]、GIN[106]忽略或简化了实际网络中节点和边的多样性和复杂性，这不足以表示数据的异质性。为了解决上述问题，关系型GNN得以提出，但是它无法捕获多跳或复杂关系。由手工制作的元路径[100]、元图[107]和元模式[34]引导的基于采样的异构GNN完全基于数据类型及其结构化连接。这一缺陷严重阻碍了在实际细粒度任务中推广此类异构GNN，比如欺诈检测[1,14]、疾病诊断[20]等–通过元路径、元图和元模式等元结构将固有实体关系外部化是不可行或低效的。以基于MIMIC-III数据集[41]的糖尿病及其疑似疾病的检测和诊断为例。值得注意的是，一部分糖尿病患者往往会出现导致青光眼的症状，而青光眼患者通常不会出现血糖、胰岛素和其他检测指标方面的问题。因此，可以很容易地定义任何两名患者之间的明确关系，例如血液试验中的高血糖分数、尿液试验中的高蛋白尿分数、视力试验中的青光眼症状、眼压试验中的高眼压等。与基于元结构的方法相比，基于实体共享的公共属性指定关系更为有用，并且不太依赖于严格的实体连接，而基于元结构的方法必须利用复杂的自动生成技术[67]或手动经验[6,36,61]。因此，为了执行下游应用程序，探索和利用源自任务特定特征的显式关系更为有效。

为了扩展GNN以支持异构图嵌入，许多方法依赖于复杂神经网络的组合[99]。比如，HetGNN[112]通过结合bi-LSTM，自注意力和类型组合从异类邻居获得多模态特征，RSHN[121]利用粗线图神经网络（CL-GNN）和消息传递神经网络（MPNN）同时学习节点和边类型嵌入。**HGT[38]利用基于相互注意、消息传递、剩余连接、特定于目标的聚合功能等的类型相关参数。**MAGNN[21]利用元路径采样、元路径内和元路径间聚合技术嵌入具有目标类型的节点。然而，它们缺乏对更实际或细粒度应用程序任务的分析，并且需要强大的领域知识来构建复杂的神经网络结构。提出的的GNN模型的可用性也应该以更方便的方式进行设计。

为此，我们提出了一种新的增强的、递归的、可伸缩的邻域选择引导的多关系图神经网络RIOGNN，它可以在保持关系相关表示的同时导航自定义神经网络结构的复杂性。对于领域任务驱动的图表示学习，我们引入多关系图来反映节点、边、属性和标签的异构性。在此，关系被称为两个节点之间的特定类型的边，通过显式公共属性或隐式语义彼此连接，比如同一个月发布的两个产品，同一导演导演的两部电影等，脱离异构信息网络（HIN）[85]，多关系图能够灵活地描述和明确区分边类型，而无需严格遵循实体关联元结构指定任意两个节点之间的语义连接。对于给定的关系，我们可以对原始图执行采样过程，以提取图中每个节点的邻居。

为了减少神经网络单元的复杂性，RioGNN在为中心节点嵌入聚合邻居信息时优化了邻居选择过程。为了避免不同类型节点之间的嵌入过度同化，我们首先采用标签感知的神经相似性度量来确定基于节点属性的最相似邻居。特别是，这是通过神经分类器实现的，该分类器将监督信号（例如，高保真注释标签）和原始节点特征进行变换，以计算节点相似性。接下来，我们进行关系感知邻居选择，以选择目标节点在强化关系中最相似的邻居，然后聚集来自不同关系的所有邻居信息，以获得最终的节点嵌入。我们通过训练阈值来优化每个神经分类器内的关系，针对异构图的不同尺度，提出了一种具有可估计深度和宽度的递归可扩展强化学习框架。具体地说，我们利用两种通用的关系感知RSRL方法——使用离散和连续策略——来确定不同关系的最佳邻居数。面对不同的数据集和应用场景，离散和连续方法通常可以提供更多的选择。RSRL不仅有助于学习区分性节点嵌入，而且使模型更易于解释，因为我们可以通过过滤阈值识别每个关系的个体重要性。基于RSRL的关系感知邻居选择器可以与用于特定场景的任何主流强化学习模型[29,33,48,84102]和邻居聚合函数[30,94]集成。

我们将上述技术与普通的GNN集成为一层RioGNN，并根据下游任务的具体要求设计多层RioGNN来学习高阶节点表示。本文主要针对具有节点级嵌入的任务，以半监督方式学习多关系节点表示。我们使用Yelp、Amazon和Mick-III数据集，将RioGNN应用于欺诈检测和糖尿病检测两项任务，评估其有效性、效率和可解释性。实验评估了如何定义下游任务，包括转换节点分类、归纳节点分类和节点聚类。结果表明，与最先进的 GNN 以及专用异构模型相比，RioGNN 的各种下游任务显着提高了 0.70%–32.78%。我们表明，我们的 RSRL 框架不仅将学习时间提高了 4.52 倍，而且在节点分类方面也实现了 4.90% 的改进。我们还在上述任务中评估了 RioGNN 对超参数的敏感性。最后，我们进行了一系列案例研究，以展示 RSRL 如何自动学习不同任务中隐式关系的重要性和参与度。

这项工作的贡献总结如下：

• 第一个基于多关系图的任务驱动GNN框架，充分利用关系采样、消息传递、度量学习和强化学习来指导不同关系内部和之间的邻居选择。
• 一种灵活的邻域选择框架，该框架采用增强的关系感知邻域选择器和标签感知神经相似性邻域度量。
• 一种递归的、可扩展的强化学习框架，通过对不同规模的图形或任务的可估计深度和宽度来学习优化的过滤阈值。
• 第一次从不同关系的重要性角度研究多关系GNN的可解释性。

我们在前期工作[15]的基础上进行了扩展，将专门针对伪装欺诈者的欺诈检测器的防伪装GNN（CARE-GNN）模型扩展到支持广泛实际任务的更通用体系结构。具体来说，改进包括：1）给出了不同实际任务下多关系图神经网络的定义、动机和目标的完整版本；将标签感知的相似性邻居度量从一层扩展到多层以选择相似的邻居； 2) 提出了一种新颖的递归和可扩展的强化学习框架，以通用且高效的方式优化每个关系的过滤阈值以及 GNN 训练过程，而不是之前的伯努利多臂老虎机方法；3）在强化学习框架下，同时利用离散和连续策略寻找不同关系的最优邻居； 4）对三个有代表性的通用数据集进行广泛的实验，不局限于欺诈检测场景。 此外，还讨论了更深入的实验结果，以证明所提出架构的有效性和效率。 我们提供多关系图表示学习结果的方差。 我们还基于提议的 RSRL 框架的过滤阈值，从一个新的角度展示了对不同关系重要性的解释。

本文的结构如下：第2节概述了预备工作和问题的提出，第3节描述了RioGNN中涉及的技术细节。第4节和第5节分别讨论了实验装置和结果。第6节在我们结束第7节的论文之前介绍了相关的工作。

2、背景和概述

2.1 问题定义

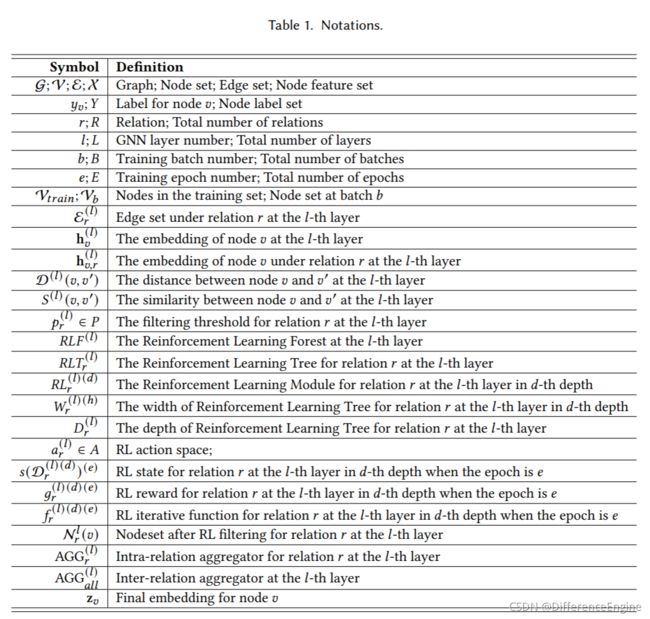
在这一部分中，我们首先定义了多关系图和多关系GNN。表1总结了本文中的所有重要符号。

定义2.1多关系图（MR-Graph).MR图定义为$\mathcal{G}=\left\{\mathcal{V},X,{\left\{{\mathcal{E}}_r\right\}|}_{r=1}^R,Y\right\}$，其中$\mathcal{V}$是节点集合$\left\{v_1,\dots ,v_n\right\}$，每一个节点$v_i$都有d维特征向量${\mathbf{x}}_i\in {\mathbb{R}}^d$，并且$X=\left\{{\mathbf{x}}_1,\dots ,{\mathbf{x}}_n\right\}$表示所有节点特征的集合。$e_{i,j}^r=\left(v_i,v_j\right)\in {\mathcal{E}}_r$是关系$r\in \{1,\cdots ,R\}$下节点$v_i$和$v_j$之间的一条边，其中$\text{R}$是边的数量。请注意，一条边可以与多个关系相关联，存在$\text{R}$种类型的边。$\text{Y}$是$\mathcal{V}$中每个节点的标签集。

多关系图直接将要分类的元素作为节点，将不同标签元素的关键关系作为多重连接，可以广泛应用于具有挑战性的分类任务。 值得注意的是，从HIN出发， 多关系图能够灵活地表征和明确区分边类型，而无需严格遵循实体关联的元结构指定任意两个节点之间的语义连接。我们通过两个实际应用来举例说明其适用性，并比较基于 MR-Graph 的建模和基于 HIN 的方法之间的差异：

• 垃圾邮件审查检测

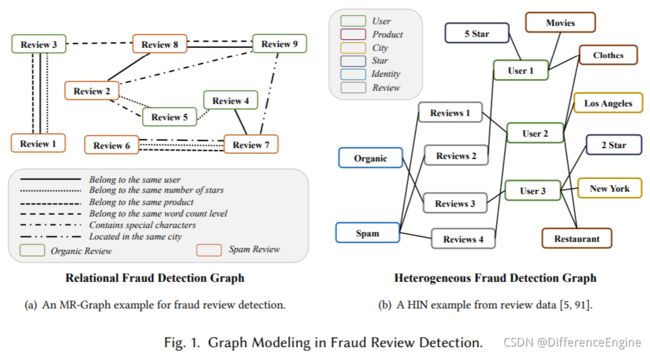
垃圾评论是指那些虚假的评论发布到产品或商家，目的是推广他们的目标。欺诈检测必须从自然的邮件中识别出垃圾邮件评论。由于垃圾评论添加了一些特殊字符或模拟良性的电子邮件行为(如一个用户发布垃圾邮件，同时保持一定频率的自然的评论)，以避免被发现，这给区分垃圾评论带来了挑战。我们将具有不同标签的注释视为节点，将不同的代表性交互视为不同类型的连接，从而构建多关系图，从而将此问题转化为双分类问题。如图1(a)所示，MR-Graph示例描述了从电子商务评论数据中提取的有机自然的评论、垃圾评论及其交互[69,82]。我们提取了两个与欺诈行为密切相关的评论之间的代表性互动，并将它们表示为不同类型的边缘——属于同一用户，具有相同的星级，针对同一月发布的同一产品，属于相同的字数水平，包含特殊字符，针对位于同一城市的产品。作为一种替代方法，传统的基于HIN的建模(图1(b))更加关注结构化连接所概述的关系。

• 疾病诊断

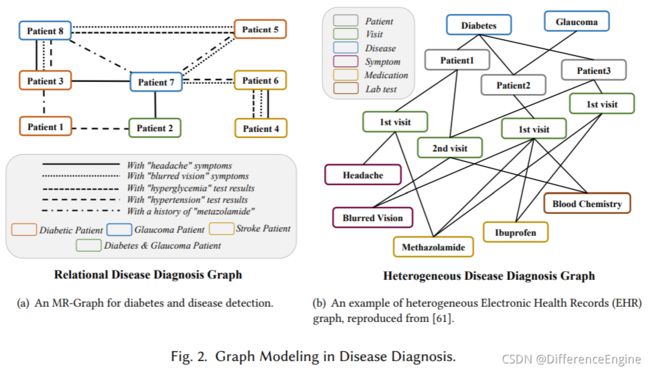
在疾病诊断任务中，糖尿病、脑卒中、青光眼是中老年人常见病，早期症状识别非常重要。 但由于这三种疾病的症状相似，临床上很难区分患者。 例如，中风的症状包括视力丧失、突然虚弱和刺痛感，这与 II 型糖尿病患者的症状相似。 此外，糖尿病的早期症状之一是由液体水平变化引起的视力模糊。 因此，眼睛可能会改变形状，干扰眼睛的聚焦能力。 虽然这种视力障碍可能表明患有糖尿病，但在青光眼患者中也是如此。 在这里，将患者作为多关系图的节点，将具有不同相似症状的患者连接成不同类型的边，可以将任务转化为多分类任务。图 2(a) 说明了用于疾病诊断的患者 MR 图。我们相信可以模拟和代表以下类型患者之间的关系：“头痛”症状，“视力模糊”症状，“高血糖”测试结果，“高血压”测试结果，“甲唑胺”病史，等更有助于糖尿病患者及其疑似疾病的诊断。甚至，两个患者之间可能存在多种关系。例如，患者5和患者8具有“视力模糊”症状和“高血压”测试结果两种共同关系。同时，以往基于 HIN 的电子健康记录 (EHR) 建模 [6,36,61] 侧重于不同属性或类型数据的关联和融合，相应的方法适用于各种疾病的诊断。此外，缺乏对某些确定疾病的细粒度分析。我们还给出了图 2(b) 中异构电子健康记录图的说明。

定义2.2多关系GNN 图神经网络 (GNN) 是一种深度学习框架，通过聚合来自其相邻节点的信息来嵌入图结构数据 [24,30,47,94]。 基于定义 2.1，我们可以从多层邻居聚合的角度根据不同的关系勾勒出 Multi-Relational GNN 的统一表述。 对于中心节点$v$，节点 $v$ 在第 l 层的隐藏或聚合嵌入称为 $h_v^{(l)}$：
$${\mathbf{h}}_v^{(l)}=\sigma \left({\mathbf{h}}_v^{(l-1)}\oplus AG{G}^{(l)}\left({\left\{{\mathbf{h}}_{v^{\prime },r}^{(l-1)}:\left(v,v^{\prime }\right)\in {\mathcal{E}}_r^{(l)}\right\}|}_{r=1}^R\right)\right),\text{\hspace{1em}(1)}$$
其中${\mathcal{E}}_r^{(l)}$表示关系$r$下第l层的边，${\mathbf{h}}_{v^{\prime },r}^{(l-1)}$指示关系$r$下邻居节点$v^{\prime }$的聚合嵌入。$AGG$表示聚合函数，它将来自不同关系的邻域信息映射到一个向量中，例如平均聚合[30]和注意力聚合[94]。$\oplus$是通过串联或求和[30]将节点$v$的信息及其相邻信息组合起来的算子。我们用输入的 d 维特征向量$x$初始化节点嵌入$h_v^{(0)}$。GNN 使用带有二元分类损失函数的部分标记节点进行训练。 我们不是直接聚合所有关系的邻居，而是将聚合部分分离为关系内聚合和关系间聚合过程。 在关系内聚合过程中，每个关系下邻居的嵌入同时聚合。 然后，在相互关系聚合过程中组合每个关系的嵌入。 最后，最后一层的节点嵌入用于预测。

2.2 问题范围和挑战

在实际应用中，我们对多关系图进行建模，以半监督学习的方式将实际问题作为节点分类任务。 根据领域知识构建多关系图后，例如图 1(a) 中的垃圾评论检测，图 2(a) 中的疾病诊断等，可以训练多关系 GNN。 然而，当我们训练更具辨别力、有效和可解释的节点嵌入时，多关系 GNN 面临三个主要挑战：

如何在 GNN 中的邻居聚合期间处理行为不当的节点（挑战 1）。输入节点的特征 X 通常基于启发式方法（例如 TF-IDF、Bag-of-Words、Doc2Vec 等）提取，容易受到以下不当行为的影响： 对抗性攻击、伪装 [15,87] 或简单的不精确特征选择。 因此，中心节点的数值嵌入往往会被行为不当的相邻节点同化。 例如，在垃圾邮件评论检测任务中，对抗性或伪装行为是不可忽略的噪声，会大大降低 GNN 学习特征表示的准确性。特征 [16,51] 或关系 [44,119] 伪装可以使行为不当和良性实体的特征相似，并进一步误导 GNN 生成无信息的节点嵌入。 在医学疾病诊断任务中，基于文本属性的特征选择可能无法提取高级或细粒度的语义，从而容易导致节点特征不精确。 因此，在应用于任何 GNN 之前，这些问题需要有效的相似性度量来过滤邻居。

如何基于相似性度量自适应地选择最合适的邻居节点（挑战2）。对于大多数实际问题，数据标注是昂贵的，我们无法通过数据标注来选择每个关系下的所有相似邻居。 直接将过滤阈值视为超参数的方法 [60,110] 不再适用于具有大量噪声或行为不当节点的多个关系图。 首先，不同的关系具有不同的特征相似度和标签相似度。 其次，不同的关系对过滤阈值有不同的精度要求。 因此，必须设计自适应采样机制，以便可以针对动态环境中的特定关系要求选择最佳数量的相似邻居。

如何以连续的方式高效地学习和优化过滤阈值（挑战 3）。 我们的初步工作[15]采用了具有固定策略的伯努利多臂老虎机框架[92]来加强过滤阈值的学习。 然而，它实质上受到状态的观察范围和手动指定策略的限制，因此过滤阈值的最终收敛结果往往是局部最优的。 此外，为了保持预测精度，面对大规模数据集，必须减小过滤阈值的调整步长或使用连续动作空间。 这个过程无疑会扩大动作空间，导致收敛周期的增加和计算量的巨大增长，可能会损失准确性。 因此，这个问题需要一个自动且高效的强化学习框架，能够快速获得充足且高质量的解决方案。

三、方法论

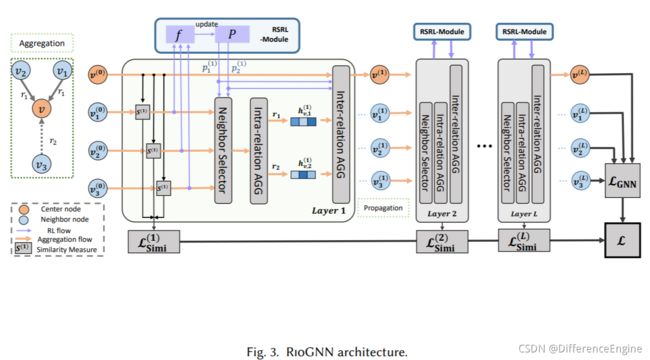
图 3 描绘了 RioGNN 的整体架构，由三个关键模块组成——标签感知相似性测量（3.1 节）、相似性感知邻居选择器（3.2 节）和关系感知邻居聚合器（3.3 节）。 此外，我们在 3.4 节中描述了整体算法和优化。

3.1 标签感知神经相似性度量

与余弦相似度 [108] 或神经网络 [108] 等无监督相似度指标相比，金融欺诈、疾病诊断等许多实际问题需要额外的领域知识（例如，高保真数据注释）来识别异常实例。 为此，我们使用领域专家的监督信号设计了参数化节点相似性度量，即标签感知神经相似性度量。 AGCN [52] 采用马氏距离加高斯核，而 DIAL-GNN [10] 采用参数化余弦相似度。 NSN [55] 将基于双线性相似性的内积和超球面学习策略统一起来。然而，它们都具有不可忽略的时间复杂性$O(\bar{k}d)$，其中$\bar{k}$表示节点的平均次数，在现实世界的图中通常非常高，d 代表特征维度。这会导致在区分节点表示学习时效率降低。

受GraphMix[95]的启发，结合全连通网络（FCN）和线性正则化，我们在RogNN的每一层采用FCN作为节点标签预测器，并将两个节点的预测结果之间的$l_1-distance$作为中间相似度的度量。它是使用 GNN 进行半监督节点分类的简单有效的正则化器。在第$l$层，当计算某一个中间节点$v$和它的邻居节点$v^{\prime }$在关系$r$下的距离时，例如边$(v,v^{\prime })\in {\mathcal{E}}_r$，我们以它们在前一层$h^{(l-1)}$中的嵌入作为输入，并应用非线性激活函数$\sigma$（在我们的工作中我们使用$tanh$），$v$和$v^{\prime }$的距离是两个嵌入的$l_1-distance$：

$${\mathcal{D}}^{(l)}\left(v,v^{\prime }\right)={\Vert \sigma \left(FC{N}^{(l)}{\mathbf{h}}_v^{(l-1)}\right)-\sigma \left(FC{N}^{(l)}{\mathbf{h}}_{v^{\prime }}^{(l-1)}\right)\Vert }_1.\text{\hspace{1em}(2)}$$

因此，两个节点的相似性可以定义为：
$$S^{(l)}\left(v,v^{\prime }\right)=1-{\mathcal{D}}^{(l)}\left(v,v^{\prime }\right).\text{\hspace{1em}(3)}$$
我们的方法的时间复杂度可以从$O(\bar{k}d)$到$O(d)$一般来说，计算成本较低，因为对于节点集$\mathcal{V}$中的每个节点，我们没有像 LAGCN [7] 那样使用其 k 个邻居与 d 维特征的组合嵌入来衡量相似性，而仅考虑 FCN 基于其自身特征预测的标签。为了使用来自标签的直接监督信号训练相似性度量，我们将第l层中FCN的交叉熵损失定义为：
$${\mathcal{L}}_{\text{Simi }}^{(l)}=\sum _{v\in \mathcal{V}}-\log \left(y_v\cdot \sigma \left(FC{N}^{(l)}\left({\mathbf{h}}_v^{(l)}\right)\right)\right).\text{\hspace{1em}(4)}$$
此外，我们将整个网络的标签感知相似性度量的交叉熵损失定义为：
$${\mathcal{L}}_{\text{Simi }}=\sum _{l=1}^L{\mathcal{L}}_{\text{Simi }}^{(l)}.\text{\hspace{1em}(5)}$$
在训练过程中，通过损失函数直接更新FCNs的相似性度量参数。 它确保可以在几批内快速选择相似的邻居，并有助于规范 GNN 训练过程。

在本小节中，我们为第2.2节中的第一个挑战提出了一种标签感知相似性检测方法。该方法基于节点标签，有效避免了实际场景中不良节点伪装带来的干扰，降低了相似度的复杂度，为后续的邻居过滤提供了稳定的基础。

3.2 相似性感知自适应邻居选择器

为了自适应地选择合适的邻居，我们设计了一个相似性感知邻居选择器来过滤源于对抗行为或不准确的特征提取的行为不端的节点。 更具体地说，对于每个中心节点，选择器利用 Top-p 采样和自适应过滤阈值来构建每个关系下的相似邻居。 由于不同层不同关系的过滤阈值往往在训练阶段动态更新，我们提出了RSRL，一种递归和可扩展的强化学习框架，以有效的方式优化每个关系的过滤阈值。

3.2.1 Top-p 采样

在聚合来自中心节点 v 及其邻域的信息之前，我们执行Top-p 采样以根据不同的关系过滤不同的邻域。关系r在第l层的滤波阈值$p_r^l\in [0,1]$表示对所有邻居的选择比例。例如，当$p_r^l=1$时，所有邻居节点都得以保留。具体来说，在训练阶段，对于关系r下的一批节点中的一个节点v，我们首先在第l层中对于边$(v,v^{\prime })\in {\mathcal{E}}_r$使用公式3计算一组相似性分数$\left\{S^l(v,v^{\prime })\right\}$。然后我们对于每个中心节点v的邻居按照$\left\{S^l(v,v^{\prime })\right\}$降序排序，并在第l层将最顶部的$p_r^l\cdot \left|\left\{S^l\left(v,v^{\prime }\right)\right\}\right|$邻居作为所选邻居，即$N_r^l(v)$。剩余节点将在当前批次被丢弃，并且不参与层内的后续聚合过程。

3.2.2 RSRL框架

以前的工作 [60,110] 将过滤阈值视为一个超参数，这对于具有大量噪声或行为不当的节点的多关系图不再有效。 为了解决这个问题，我们的前期工作[15]采用了具有固定学习策略的伯努利多臂老虎机框架[92]，并动态更新了过滤阈值。 然而，这种方法的有效性在很大程度上受到状态观察范围和手动指定策略的限制。 因此，过滤阈值的最终收敛结果往往是局部最优的。 面对更大规模的数据集，保持预测精度还需要减小过滤阈值的调整步长。 这个过程会增加收敛epoch的数量，带来计算量的增加和精度的损失。

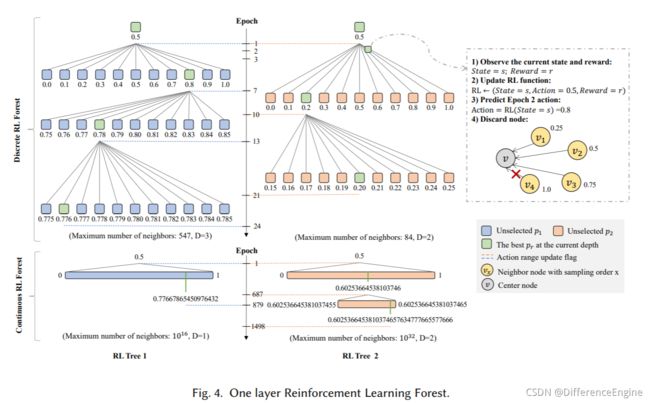
概述为了解决这些问题，我们在传统的基于强化学习的方法 [43,49,62] 的基础上，提出了一种新颖的递归和可扩展强化学习框架 RSRL，不仅可以通过学习环境更新策略，而且可以使用递归结构快速准确满足不同关系的精度要求。 图 4 描绘了基于森林的学习架构。 一棵树在每个epoch中的具体过程如右图所示，其中s和r分别代表上一个epoch之后的状态和奖励，a（图中例子为0.5）代表当前epoch中预测的动作。 我们将 RSRL 制定为 L 层强化学习 (RL) 森林，并将第 l 层森林定义为：
$$RL{F}^{(l)}={\left\{RL{T}_r^{(l)}\right\}|}_{r=1}^R={\left\{{\left\{R{L}_r^{(l)(d)}\right\}|}_{d=1}^{D_r^{(l)}}\right\}|}_{r=1}^R,\text{\hspace{1em}(6)}$$
$RL{F}^{(l)}$实际上是指在第l层获得最佳关系滤波阈值组合的过程。每个关系独立地以自适应的深度$D_r^{(l)}=\lceil {\log }_{\alpha }{k}_r\rceil$和宽度$W_r^{(l)(d)}=\frac{1}{{\alpha }^d}$构造RL树$RL{F}^{(l)}$。$\alpha$是深度优先和宽度优先的权重参数，$k_r^{(l)}$是关系 r 中包含在节点中的最大邻居数。$RL{F}^{(l)}$执行强化学习$R{L}_r^{(l)(d)}$在每个深度以精度$W_r^{(l)(d)}$过滤阈值。在第l层，$RL{F}^{(l)}$ 通过多次 RL 递归获取精度高于前一关系深度 r 的邻居节点的最佳过滤阈值 $p_r^{(l)(d)}$，直到在深度 $D_r^{(l)}$ 处找到最大精度要求的阈值。$RL{F}^{(l)}$ 递归过程表示为：
$$p_r^{(l)(d)}\stackrel{R{L}_r^{(l)(d)}}{⟵}\left\{p_r^{(l)(d-1)}-\frac{W_r^{(l)(d)}}{2},p_r^{(l)(d-1)}+\frac{W_r^{(l)(d)}}{2}\right\}.\text{\hspace{1em}(7)}$$
其中 $p_r^{(l)(d)}$ 表示当 RL 树在第 l 层的深度为 d 时，关系r中要丢弃的邻居节点的最佳比例。每个深度的RL模块的学习范围是前一个深度选择的滤波器阈值$p_r^{(l)(d-1)}$的$\pm \frac{W_r^{(l)}}{2}$以内的值。当递归过程达到最大深度$D_r^{(l)}$时，我们得到第l层关系r的最终过滤阈值$p_r^{(l)}$ 。考虑到复杂度与动作空间[17]的大小呈线性关系，该过程对RL动作进行了精确递归，可以将时间从$O\left(k_r\right)$减少到$O\left(\alpha {\log }_{\alpha }{k}_r\right)$，其中$\alpha \in [1,k_r]$并且$k_r$为 关系r下的最大节点度。

强化学习过程细节 我们将RL模块表示为一个关系的过滤阈值的马尔科夫决策过程 $MDP<A,S,R,F>$.$A$和$S$分别是作用空间和状态空间;$R$为奖励函数，$F$为迭代函数和终止条件。为了更好地处理不同规模和不同场景的数据集，我们将解决方案分为两类：离散强化学习(D-RL)和连续强化学习(C-RL)。

• 动作 当关系 r 在第 l 层的深度 d 时，我们通过收集所有动作$a_r^{(l)(d)}\in \left\{p_r^{(l)(d-1)}-\frac{W_r^{(l)(d)}}{2},p_r^{(l)(d-1)}+\frac{W_r^{(l)(d)}}{2}\right\}$来定义$R{L}_r^{(l)(d)}$的动作空间 A。离散方案 D-RL 将动作空间平均划分为 $\alpha$ 个离散动作。 在连续方案C-RL中，第l深度的动作空间是一个宽度为$W_r^{(l)(d)}$的连续浮点数。两种动作空间的兼容性可以有效适应多种强化学习算法。 由于对中小规模数据集的过滤阈值精度要求不高，动作离散化可以在满足基本精度要求的同时减少动作探索的次数[45]，保证高效访问高性能区域。 对于具有大规模邻居的数据集，大量满足高精度要求的离散动作会影响学习效果[17]。 我们建议将过滤阈值推广到连续动作空间，以通过多次减少空间范围来提高大规模数据集的准确性。

• 状态 由于无法将 GNN 的分类损失直接感知为环境状态，我们通过标签感知的距离度量（式（2））计算每个 epoch 的平均节点距离作为状态。 在第 e 个 epoch 的第 l 层，第 d 个深度的关系 r 的状态 s 为：

$$s_r^{(l)(d)(e)}=\frac{{\sum }_{\left(v,v^{\prime }\right)\in {\mathcal{E}}_r^{(l)(d)(e)}{\mathcal{D}}^{(l)}{\left(v,v^{\prime }\right)}^{(e)}}}{\left|{\mathcal{E}}_r^{(l)(d)(e)}\right|},\text{\hspace{1em}(8)}$$

其中 ${\mathcal{E}}_r^{(l)(d)(e)}$是在关系 r 下在第 e 代epoch的第 l 层和第 d 层深度中过滤的边缘集。

• 奖励 对于每个关系，目标是确定一个过滤阈值 $p_r^{(l)(d)}$，以便选择的邻居节点和中心节点尽可能接近。 因此，我们使用相似度（公式（3））作为奖励函数中的决定性因素。 在第 e 个 epoch 的第 l 层，关系 r 与第 d 个深度的奖励 g 为：

$$g_r^{(l)(d)(e)}=\tau \cdot \left(\frac{{\sum }_{\left(v,v^{\prime }\right)\in {\mathcal{E}}_r^{(l)(d)(e)}{\mathcal{S}}^{(l)}{\left(v,v^{\prime }\right)}^{(e)}}}{\left|{\mathcal{E}}_r^{(l)(d)(e)}\right|}\right),\text{\hspace{1em}(9)}$$

其中$\tau$为权重参数，${\mathcal{E}}_r^{(l)(d)(e)}$的含义与状态中的定义相同。

• 迭代与终止 在开始每个 epoch 之前，RL 观察上一个动作$a_r^{(l)(d)(e-1)}$ 的 epoch 之后环境的状态 $s_r^{(l)(d)(e)}$，并获得奖励 $g_r^{(l)(d)(e-1)}$。然后用它们来更新迭代函数（广义上指的是策略迭代的函数或强化的值迭代过程） 学习）$f$。 每个$R{L}_r^{(l)(d)}$的迭代函数如下：

$$f_r^{(l)(d)}\leftarrow s_r^{(l)(d)(e-1)},s_r^{(l)(d)(e)},a_r^{(l)(d)(e-1)},g_r^{(l)(d)(e-1)}.\text{\hspace{1em}(10)}$$

然后我们可以使用迭代函数从当前状态$s$预测动作$a$，也就是过滤阈值：
$$p_r^{(l)(d)(e)}=a_r^{(l)(d)(e)}=f_r^{(l)(d)}\left(s_r^{(l)(d)(e)}\right).\text{\hspace{1em}(11)}$$
这里，对于动作的输出，使用分类类型的激活函数在D-RL中表示它们，比如softmax。 而在C-RL中，我们使用返回值类型的激活函数来表示它们，比如$tanh$。 由于我们提出的是一个适用于各种强化学习算法的通用框架，因此迭代函数的具体定义取决于实际算法。 我们在 5.3 节中测试了 RSRL 框架对各种主流强化学习算法的适用性。为了提高均衡效率，我们假设只要相同的动作在当前精度$W_r^{(l)(d)}$下连续出现 三次，RL 就会被终止。 具体来说，在第 e个epoch的第 l 层，终止条件为 第 d 个深度中的关系 r 定义如下：
$$\{\begin{array}{ll}{\left\{p_r^{(l)(d)(i)}-p_r^{(l)(d)(i-1)}=0\right\}|}_{i=e-1}^e& D-Rl,\text{ where }e>2.\\ {\left\{\left|p_r^{(l)(d)(i)}-p_r^{(l)(d)(i-1)}\right|<W_r^{(l)(d)}\right\}|}_{i=e-1}^e& C-RL,\text{ where }e>2.\end{array}\text{\hspace{1em}(12)}$$
我们将这种深度切换条件或终止条件正式定义为$\text{ deep switching number }=3$，并在第 第5.5 节中讨论参数敏感性。

为了获得更好的训练结果，我们使用白盒方法在训练过程中同步测试结果，并在对同一关系开始新一轮 RL 之前验证该轮的收敛值是否最佳。 如果该值为负数，则在新一轮优化中审核历史版本中性能较好的过滤阈值，作为新一轮动作范围的依据。 对于这种回溯机制，我们将在第5.5 节中进行敏感性实验。

在本小节中，我们克服了第 2.2 节中提到的第二个和第三个挑战。 具体来说，我们使用上一小节中的相似性度量对每个关系的邻居进行 Top-p 采样。 在强化学习的基础上，我们使用agent与环境进行交互，做出不同的关系，从而获得不同的阈值组合。 这种自适应方法无需数据标注的帮助。 此外，为了在保证精度的同时满足不同关系的精度要求，我们提出了一个递归优化框架。

3.3 关系感知加权邻居聚合器

基于为每个关系选择相似的邻居，下一步是聚合关系之间的所有这些邻居信息，以进行全面的嵌入。 以前的方法采用注意机制 [31,58,97,117] 或加权参数 [59] 在聚合过程中学习关系权重。 为了在保留关系重要性信息的同时降低计算成本，我们直接使用由 RSRL 过程学习的最佳过滤阈值 $p_r^{(l)}$ 作为相互关系聚合权重。 形式上，对于中心节点 v，在第 l 层的关系 r 下，关系内邻居聚合可以定义如下：
$${\mathbf{h}}_{v,r}^{(l)}=\mathrm{ReLU}\left(AG{G}_r^{(l)}\left(\left\{\oplus {\mathbf{h}}_{v^{\prime }}^{(l-1)}:v^{\prime }\in {\mathcal{N}}_r^l(v)\right\}\right)\right),\text{\hspace{1em}(13)}$$
其中$\oplus$表示均值聚合器 $AG{G}_r^{(l)}$ 的嵌入按位求和操作，$N_r^l(v)$ 是指在第 l 层在关系 r 下通过 公式(10) 获得的顶部$p_r^{(l)}$节点的集合。中心节点v的关系内邻域聚合的目的是将上一层关系r下的所有邻域信息聚合到嵌入向量$h_{v,r}^{(l)}$中。

进一步地，我们将关系间聚合定义如下：
$${\mathbf{h}}_v^{(l)}=\mathrm{Re}LU\left({\mathbf{h}}_v^{(l-1)}\oplus AG{G}^{(l)}\left({\left\{\oplus \left(p_r^{(l)}\cdot {\mathbf{h}}_{0,r}^{(l)}\right)\right\}|}_{r=1}^R\right)\right),\text{\hspace{1em}(14)}$$
其中$h_{v,r}^{(l)}$ 表示第 l 层的关系内邻居嵌入， $AG{G}_r^{(l)}$ 可以是任何类型的聚合器。 这里我们直接使用RSRL框架优化的$p_r^{(l)}$作为聚合权重，在5.1.1节和5.2.1节对其他类型的聚合方法进行实验。

在本小节中，为了更好地处理不正确的节点来应对第 2.2 节中的挑战 1，我们将聚合过程分为相互关系和内部关系，并使用过滤的邻居节点和不同关系的过滤阈值来加强影响聚合期间良性节点的数量。

3.4 整合

我们将节点$v$的最终嵌入表示为${\mathbf{z}}_v={\mathbf{h}}_v^{(L)}$，这是 RioGNN 在最后一层的输出。 我们还将 GNN 在节点分类任务中的损失函数定义为交叉熵损失函数：
$${\mathcal{L}}_{GNN}=\sum _{v\in \mathcal{V}}-\log \left(y_v\cdot \sigma \left(ML{P}^{(l)}\left({\mathbf{z}}_v\right)\right)\right).\text{\hspace{1em}(15)}$$
结合等式 4 中节点分类的损失函数和相似性度量的损失函数，我们定义 RioGNN 的最终损失函数如下：
$${\mathcal{L}}_{\text{RIOGNN }}={\mathcal{L}}_{GNN}+{\lambda }_l\sum _{l=1}^L{\mathcal{L}}_{\text{Simi }}^{(l)}+{\lambda }_{\ast }\Vert \Theta {\Vert }_2,\text{\hspace{1em}(16)}$$
其中$\lambda$和${\lambda }_{\ast }$是权重参数，并且$\Vert \Theta {\Vert }_2$是所有模型参数的L2范数。

最后，基于上述研究，算法 1 概述了所提出的 RioGNN 的训练过程，该过程采用建立在现实世界实际问题上的任何给定输入多关系图。 我们采用小批量训练技术 [26] 来处理过大的真实世界图。在每个时期训练 RioGNN 模型之前，我们初始化标签感知相似性模块、关系感知邻居选择模块和关系感知邻居聚合器模块的参数。 对于每一批节点，我们首先使用等式（4）计算邻居相似度，然后利用 top-p 采样来过滤邻居。此后，我们计算内部关系嵌入（通过使用方程（13））和相互关系嵌入（通过使用方程（14）），并定义当前的损失函数（通过使用方程（16）） 批。 在 RSRL 模块中，我们根据每个关系的每一层的最大深度依次分配$H$ RL 模块。在每个 RL 模块中，每个 epoch 将通过方程（8) 观察环境状态并通过方程(9) 获得奖励。 然后算法通过方程(10)更新迭代函数，并通过更新后的迭代函数通过方程(11)预测当前epoch的过滤阈值。 当一个 RL 模块通过方程(12) 达到收敛条件而不以最大深度为目标时，我们将递归地进行下一个深度 RL，直到所有 RL 模块完成。

RioGNN的时间复杂度 算法1的总体时间复杂度是$O\left(|\mathcal{E}|\cdot \max \left({\left\{\alpha {\log }_{\alpha }{k}_r\right\}|}_{r=1}^R\right)\right)$，其中$|\mathcal{E}|$是边的数量，$\alpha$是深度优先和宽度优先的权重参数，$k_r$是与r相关的节点中包含的最大邻居数。这里，$O(|\mathcal{E}|)$是一个epoch的时间复杂度。具体来说，相似性度量（算法 1 中的第 10 行）和聚合（算法 1 中的第 13-15 行）总共需要 $O(|\mathcal{E}|d+|\mathcal{V}|(\bar{k}d+d))=O(|\mathcal{E}|)$，其中$\bar{k}$是平均节点度数$|\mathcal{V}|$是节点数量。RSRL模块（算法1中的第21-29行）采用$O(|\mathcal{E}|d)=O(|\mathcal{E}|)$每个交叉熵损失函数（算法1中的第8行和第16行）取$O(|\mathcal{V}|)$另外，epoch数受强化学习的动作空间影响，达到收敛所需的epoch数与几个关系$\max \left({\left\{\alpha {\log }_{\alpha }{k}_r\right\}|}_{r=1}^R\right)$中需求最大的动作空间有关。

四、实验组织

在接下来的两节，我们进行实验来评估和测试RioGNN。实验设置主要围绕以下六个问题展开：

• $Q1:$我们如何在不同的场景中构建多关系图（第4.2节）？
• $Q2:$RioGNN在欺诈检测任务中的有效性、效率和可解释性（第5.1节）。
• $Q3:$RioGNN在疾病检测任务中的有效性、效率和可解释性（第5.2节）。
• $Q4:$不同的任务需求如何匹配通用RSRL框架（第5.3节）？
• $Q5:$我们的模型在集群任务和归纳学习中表现如何（第5.2.1节、第5.1.1节和第5.4节）？
• $Q6:$讨论超参数敏感性和对模型的影响（第5.5节）。

4.1 实验设置

我们使用 Pytorch 实现 RioGNN。 所有实验都在 Python 3.7.1 和具有 32GB RAM 的 NVIDIA V100 NVLINK GPU 上运行。 操作系统是 Ubuntu 20.04.2。 为了提高训练效率并避免过拟合，我们采用小批量训练和欠采样技术来训练 RioGNN 和其他基线。 具体来说，在每个小批量下，我们随机抽样与正实例数量相同的负实例数量。

4.2 数据集与图构建

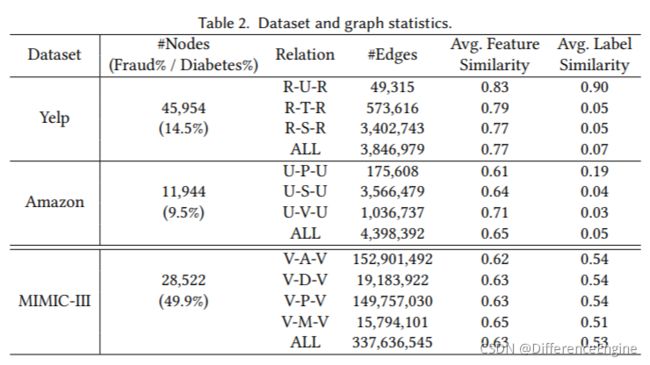
我们为两个任务场景和三个数据集的实验构建了不同的多关系图。 表2列出了不同数据集节点和关系的各种统计信息。 除了不同场景下的节点数和噪声节点的比例（Fraud%，Diabetes%），我们还给出了不同关系的边数。 对于每个数据集中的每个关系，我们根据相邻节点的特征向量的欧氏距离（范围为0到1）计算相邻节点的特征相似度，并对平均特征相似度进行归一化。 表2 的最后一列显示了每个关系的平均标签相似度，它是根据两个连接的节点是否具有相同的标签来计算的。

4.2.1 欺诈检测任务

我们分别在 Yelp 数据集和 Amazon 数据集上执行二分类任务、垃圾邮件评论检测和欺诈用户检测。

YELP: 收集自美国最大的商业评论网站 Yelp.com 发布的内部数据集。我们使用 [69] 收集和使用的 YelpChi 数据集的一个子集。该子集包含 45,954 条用户对芝加哥地区酒店和餐馆的评论。评论已被 Yelp 过滤（垃圾邮件）和推荐（合法）。数据集除了包含用户和产品之间的关系信息外，还包含各种元数据，包括评论的文本内容、时间戳和星级。我们使用了32个人工特征，包括所有产品评论的排名顺序、与产品平均值的绝对评分偏差、是否是用户唯一的评论、所有大写单词的百分比、大写字母的百分比、评论的长度、第一人称代词的比例，感叹句的比例，以及[82]中使用的主词比例，客观词比例等作为Yelp数据集的原始节点特征。对于特定的关系，由于之前的研究 [69,82] 已经表明意见欺诈者（即垃圾邮件发送者）在用户、产品、评论文本和时间方面是相互关联的，我们使用评论作为图中的节点并设计了三种关系：

• R-U-R：它连接同一用户发布的评论。
• R-T-R：它连接同一个月发布的同一产品下的两个评论。
• R-S-R：它连接同一产品下具有相同星级（1-5星级）的评论。

Amazon: 是亚马逊产品数据集的子集 [66]。亚马逊数据集包含超过 34,000 条消费者评论，我们从中提取了乐器类别下的 11,949 条产品评论。此外，与[115]类似，我们将有用投票率大于 80% 的用户标记为良性实体，将有用投票率小于 20% 的用户标记为欺诈实体。在节点特征选择方面，我们使用了25个人工特征，包括评分产品数量、用户名长度、用户给出的每个评分等级的数量和比例、正面和负面评论的比例、用户的评分,用户获得的有用和无用票总数,有用票和无用票的比例,以及平均值,有用和无用票的中位数,最小和最大有用和无用票数,用户之间的天数[115] 中作为亚马逊数据集的原始节点函数使用的第一个和最后一个评分、相同的日期指示符、评论文本情绪等。对于具体的关系，我们为多关系图设计了三种关系，如下所示：

• U-P-U：它连接用户至少查看一个相同的产品。
• U-S-V：它连接一周内至少有一个相同星级的用户。
• U-V-U：它将所有用户中互评文本相似度最高的5%（由TF-IDF衡量）的用户连接起来。

4.2.2 糖尿病诊断任务

我们在处理后的MIMIC-III数据集资源上执行糖尿病诊断的二分类任务。

MIMIC-III: 是一个公开可用的数据集 [25,42]，包含 46,520 名重症监护病房 (ICU) 患者超过 11 年的健康记录。我们总共提取了 28,522 次患者就诊，每条记录包含年龄、诊断、微生物学、程序、语料库等。我们使用 [61] 收集和使用的 MIMIC-III 数据集的一个子集，并在此基础上为我们的任务构建多关系图。对于每个患者和访问，都有一个唯一的 ID 来跟踪其相应的信息。根据诊断代码，我们将病历标记为糖尿病或非糖尿病。如 [63] 中建议的那样，使用阈值 15、30 和 64 将年龄分成组。程序和诊断被映射到相应的 ICD-9-CM 代码中。具有培养阳性结果的微生物学测试被映射到生物体的名称中。我们利用以上四个字段，在访问节点之间形成不同的关系来构建异构图。在之前的医学表征学习的基础上，我们基于从入院记录中获得的医学语料来获取每个节点的特征表征。由于医学知识领域的复杂性，我们适当扩大了关系的选择范围，以进一步测试我们的RSRLFramework对伪装邻居的过滤性能。对于具体的关系，由于之前的工作[6]已经详细描述了不同领域的概念，我们在此基础上为多关系图设计了四种关系，如下所示：

• V-A-V：它连接相同年龄组的就诊。
• V-D-V：它连接具有相同诊断的就诊。
• V-P-V：它连接具有至少一个相同程序代码的就诊
• V-M-V：它连接具有至少一个相同微生物学代码的就诊

4.2.3 数据集的评估

我们从节点分布、边缘分布、特征相似度和标签相似度这四个指标来衡量不同的数据集。 可以观察到，在欺诈检测任务中，Yelp 和 Amazon 的欺诈节点只有 14.5% 和 9.5%，而 MIMIC 的比例更为均衡。 此外，三个数据集的不同关系都有不同的数量级和不均匀的边缘分布。 此外，在 Yelp 和 Amazon 数据集中，具有不同关系的边具有均衡的特征相似度，但现有边具有较高的特征相似度和较低的标签相似度。 例如，R-T-R 的平均特征相似度为 0.79，但标签相似度仅为 0.05。 这表明欺诈者成功伪装成良性实体，需要更有效的方法来识别它。 总的来说，这些特征挑战了模型在不同情况下从数据集中学习的能力。具体来说，Yelp 和亚马逊专注于挑战不均衡数据集的能力。 Mimic 更注重过滤高密度邻居节点的能力。 MIMIC在每个关系下的关系矩阵更密集，比Yelp和Amazon高一个数量级。

4.3 基线和变体

4.3.1 基线

为了验证 RioGNN 在减轻类似任务和模型之间相互干扰方面的有效性，我们将其与半监督学习设置下的传统和最新 GNN 基线进行比较。 对于所有基线模型，我们使用开源实现。

前三个模型与传统的 GNN 基线进行比较。

• GCN[47]：是谱图卷积方法的代表，它为神经网络模型建立了一个简单且表现良好的分层传播规则。 该规则直接在图上运行，并使用切比雪夫多项式的一阶逼近来完成一个高效的图卷积架构。
• GAT[94]：是一种神经网络架构，结合了在图结构数据上运行的注意力机制。 它使用屏蔽的自注意力层来重视节点之间的边缘，帮助模型学习结构信息，并为邻域中的不同节点分配不同的权重，而无需进行昂贵的计算和预定义。
• Graph-SAGE[30]：是一种具有代表性的非谱图方法。对于每个节点，该方法提供了一个通用的归纳框架，对其局部邻居的特征进行采样和聚合以生成嵌入，而不是训练单独的嵌入。它提高了GNNs的可伸缩性和灵活性。

第二组的十个基线是处理多关系数据或本文中使用的数据集的最新 GNN 模型。

• RGCN[83]：是一种关系型GCN模型，它使用高斯分布作为隐藏层节点特征表示，并依赖注意机制自动分配每个邻居的权重以聚合邻居信息。
• GeniePath[58]：是一种可扩展的图神经网络模型，用于学习在置换不变图数据上定义的神经网络的自适应接受域。 通过对自适应路径层的广度和深度探索，该模型可以感知相邻节点的重要性，并提取和过滤从邻域收集的信号。
• Player2Vec[117]：是一种AHIN表示学习模型，将属性异构信息网络（AHIN）映射到多视图网络，对不同设计元路径描述的用户之间的相关性进行编码，并使用注意力机制融合来自每个视图的嵌入以形成最终节点表示。
• SemiGNN[97]：是一种半监督的注意力图神经网络，其中设计了分层注意力机制。 通过节点级注意力整合邻域信息，通过视图级注意力整合多视图数据，从而获得更好的准确性和可解释性。
• GAS[51]：使用异构图和同构图来捕获评论的局部和全局上下文，并且是基于元路径的异构 GCN 模型。 在我们的场景中，元路径是从关系中枚举出来的。
• FdGars[98]：基于多个关系构建一个单一的同构图，并使用 GNN 来聚合邻域信息。 与我们的工作相比，该模型缺乏邻域选择。
• GraphConsis[60]：是一种将上下文嵌入与节点相结合、过滤不一致的邻居并生成相应的采样概率的模型。 使用关系注意机制融合来自每个关系的采样节点的嵌入。
• HAN[100]：是一个分层注意力网络，通过不同的元路径聚合邻居信息。 尽管输入数据是异构的，但在我们的场景中元路径是对称的（即端节点是相同类型的），因此该模型被视为同构模型。
• GCT[13]：是使用 Transformer 学习隐式 EHR 结构的基本模型。 利用统计数据指导结构学习过程，解决了现有方法需要完整对接结构信息的问题。 具体来说，他们使用attention mask和先验知识来引导self-attention学习隐藏的EHR结构，即使在结构信息缺失的情况下，他们也可以一起学习EHR的底层结构。
• HSGNN[61]：是一种基于异构医学图的半监督图神经网络，它结合了基于元路径实例的相似矩阵和self-attention机制。

第三组的两个基线是最新的强化学习引导的 GNN 模型。 我们分别使用原始异构图和提出的多关系图作为这些模型的输入。

• GraphNAS[61]：可以通过强化学习自动搜索合适的图神经架构。 该模型使用循环网络生成描述图神经网络架构的可变长度字符串，然后使用强化学习训练循环网络以最大化生成架构的预期精度。
• Policy-GNN[49]：是一个元策略框架，它自适应地学习聚合策略以对不同节点的聚合的不同迭代进行采样。 为了加速学习过程，我们还使用缓冲机制来启用批量训练和参数共享机制，以降低训练成本。

最后一个基线来自本文的初步版本。

• CARE-GNN[15]：一层标签感知的相似性度量用于查找信息丰富的相邻节点。 然后使用**伯努利多臂老虎机(BMAB) 机制**来探索每个关系的最佳邻居数。

在这些基线中，GCN、GAT、GraphSAGE和 GeniePath在同构图（即表 2 中的所有关系）上运行，其中所有关系合并在一起。 ${\text{GraphNAS}}^H$ 和${\text{Policy-GNN}}^H$ 在原始异构图上运行。 其他模型在多关系图上运行。 在多关系图上，它们以其自己的方法处理来自不同关系的信息。

4.3.2 变体

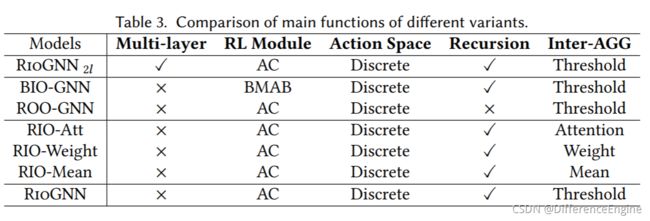
我们已经实现了 RioGNN 模型的许多变体。 不同变体的配置如表 3 所示。 具体而言，模型变体的设置主要围绕三个模块的关键机制展开：标签感知相似性度量、相似性感知邻居选择器和关系感知邻居聚合器。

第一个是未扩展多层版本的标签感知相似性度量部分的变体。

• ${\text{RioGNN}}_{2l}$：它使用带有离散策略的演员-评论家（AC）算法递归选择不同关系的过滤阈值，并使用过滤阈值作为关系权重来聚合不同关系之间的邻居。 但是标签感知相似性度量使用 2 层结构进行邻居选择。

接下来的两种方法是根据相似性感知邻居选择器模块的变化。

• BIO-GNN：该变体是一种单层相似性感知邻居选择方法，并使用过滤阈值在关系之间进行聚合。而离散策略的**伯努利多臂老虎机(BMAB) **算法用于递归选择关系的过滤阈值。
• ROO-GNN：该变体是一种具有单层相似性感知邻居选择的方法，并使用过滤阈值进行关系之间的聚合。 但是离散策略的演员-评论家算法用于直接选择关系的过滤阈值。 这种方法可以看作是 RioGNN 的非递归（单深度）版本。

以下三种变体之间的差异反映在关系感知邻居聚合器的不同关系之间的聚合方法中。

• RIO-Att：该变体使用单层相似度感知进行邻居选择，并使用带有离散策略的演员-评论家算法递归选择不同关系的过滤器阈值。 但是它在聚合不同关系之间的邻居时选择了Attention [94]的方法。
• RIO-Weight：该变体使用单层相似度感知进行邻居选择，并使用带有离散策略的演员-评论家算法递归选择不同关系的过滤器阈值。 但是它在聚合不同关系之间的邻居时选择了Weight [59]的方法。
• RIO-Mean：该变体使用单层相似度感知进行邻居选择，并使用带有离散策略的演员-评论家算法递归选择不同关系的过滤器阈值。 但是在聚合不同关系之间的邻居时，它选择了Mean [30]的方法。

4.3.3 强化学习变体

为了更好地讨论本文框架对多种强化学习算法的适应性，我们对不同强化学习算法的两个动作空间（离散和连续）进行了实验。

前三个强化学习模型基于离散动作空间。 即在构建强化学习森林的过程中，采用离散过滤阈值作为强化学习的动作类型。

• AC[48]：Actor-Critic（AC）方法结合了基于价值的方法和基于策略的方法的优点。 采用基于值的方法训练Q函数，提高样本利用效率。 使用基于策略的方法来训练策略，适用于离散和连续的动作空间。 这种方法可以看作是连续动作空间中基于值的方法的扩展，或者是对基于策略的方法的改进，以减少采样方差。
• DQN[68]：深度Q学习（DQN）是一种基于时间差分、基于值的off-policy强化学习方法。DQN通过函数逼近近似地解决了Q-Learning方法在面对高维状态和行为时的维灾难问题。此外，传统的Q-Learning方法使用带有时间序列的样本进行单步更新，并且$Q$值由采样连续性更新。DQN使用随机数据进行梯度下降，这是由于尝试和错误收集了大量样本，这可以打破数据之间的相关性。
• PPO[84]：近端策略优化 (PPO) 在策略梯度 (PG) 的基础上限制更新步长，以防止策略崩溃并使算法上升更稳定。

接下来的四个强化学习模型基于连续动作空间。即，在构建强化学习森林的过程中，使用连续过滤阈值作为强化学习的动作类型。

• AC[48]：我们使用 AC 方法在离散动作空间和连续动作空间中进行变体实验。
• DDPG[54]：Deep Deterministic Policy Gradient (DDPG) 是 DeepMind 开发的一种用于连续控制的 off-policy 算法，比 PPO 具有更高的样本效率。 DDPG 训练确定性策略，即每个状态只考虑一个最优动作。
• SAC[34]：Soft Actor-Critic (SAC) 是一种为最大熵强化学习开发的off-policy算法。 与 DDPG 相比，Soft Actor-Critic 使用随机策略，相对于确定性策略具有一定优势。 Soft Actor-Critic 在公共基准测试中取得了优异的成绩，可以直接应用于真实机器人。
• TD3[22]：Twin Delayed Deep Deterministic policy gradient (TD3) 是一种时间差分、基于策略的策略梯度强化学习方法。 TD3 是 DDPG 的优化版本。 它使用两组网络来估计$Q$值，使用相对较小的一组作为更新目标。

4.4 模型训练

我们使用统一嵌入大小（64），批量大小（Yelp为1024，Amazon和MIMIC-III为256），学习率（0.01），相似损失权重$({\lambda }_1=2)$，L2正则化权重$({\lambda }_2=0.001)$适用于所有模型。除特别说明的对比实验外，其他未说明的实验均采用40%的训练比例，欠采样比例1:1，深度切换次数3，深度优先和广度优先$\alpha$的权重参数为10，并采用了具有回溯功能的单层相似性感知结构。对于强化学习模型，我们使用 gamma (0.95)、学习率 (0.001) 作为统一参数，缓冲容量 (5)、批量大小 (1) 作为 DDPG、DQN、SAC 和 TD3 的参数。 我们在第 5.5 节中对深度切换数、回溯设置、欠采样率进行了敏感性研究。 此外，我们还在5.3节讨论了深度优先和广度优先的权重参数，在5.1节和5.2节讨论了训练比率。

4.5 评估指标

我们利用 ROC-AUC (AUC) [93] 和 Recall 来评估所有分类器的整体性能。 AUC是根据所有实例的预测概率的相对排序计算的，可以消除不平衡类的影响。 召回定义为：
$$\text{ Recall }=\frac{TP}{TP+FN},\text{\hspace{1em}(17)}$$
其中$TP$是真正例，$FN$是假负例。AUC的定义是：
$$AUC=\frac{1}{2}\sum _{i=1}^{m-1}\left(x_{i+1}-x_i\right)\left(y_i+y_{i+1}\right),\text{\hspace{1em}(18)}$$
其中$y$是真正例率$\left(TPR=\frac{TP}{TP+FN}\right),$$x$是假负例率$\left(FPR=\frac{FP}{FP+TN}\right)$。$FP$是假正例，$TN$是真负例。

在聚类任务中，我们使用归一化互信息（NMI）和调整后的兰德指数（ARI）作为性能指标。ARI的定义如下：
$$ARI=\frac{{\sum }_{ij}\left(\begin{array}{l}{n}_{ij}\\ 2\end{array}\right)-\left[{\sum }_i\left(\begin{array}{l}{a}_i\\ 2\end{array}\right){\sum }_j\left(\begin{array}{l}{b}_j\\ 2\end{array}\right)\right]/\left(\begin{array}{l}n\\ 2\end{array}\right)}{\frac{1}{2}\left[{\sum }_i\left(\begin{array}{c}{a}_i\\ 2\end{array}\right)-{\sum }_j\left({}_2^{b_j}\right)\right]-\left[{\sum }_i\left(\begin{array}{c}{a}_i\\ 2\end{array}\right){\sum }_j\left(\begin{array}{c}{b}_j\\ 2\end{array}\right)\right]/\left(\begin{array}{c}n\\ 2\end{array}\right)},\text{\hspace{1em}(19)}$$
其中，每个$n_{ij}$表示同时位于${\text{class}}_i$和${\text{cluster}}_j$中的节点数量，$a_i$表示中的节点${\text{class}}_i$数量，$b_j$表示${\text{cluster}}_j$中的节点数量。NMI的定义如下：
$$NMI=\frac{I(\omega ;C)}{[H(\omega )+H(C)]/2},\text{\hspace{1em}(20)}$$
其中$I$是互信息，$H$是熵。

在归纳学习中，为了更好地衡量学习的有效性，我们在AUC和回忆这两个指标之后增加了F1指标。F1定义为：
$$F1=2\cdot \frac{\text{ Precision }\cdot \text{ Recall }}{\text{ Precision }+\text{ Recal }},\text{\hspace{1em}(21)}$$
其中 $Precision=\frac{TP}{TP+FP}$，$TP$是真正例，$FP$是假正例。

五、结果与讨论

5.1 欺诈检测任务的总体评估

5.1.1 准确性分析

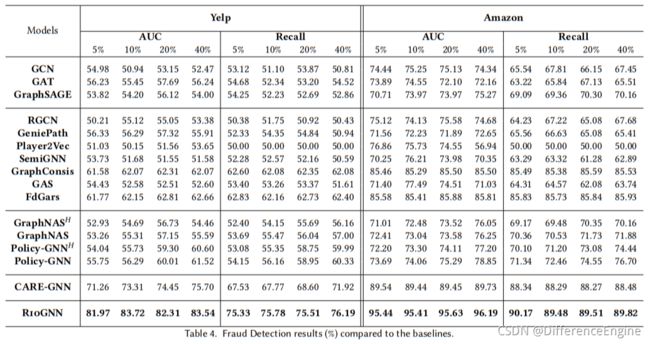
在本节中，我们进行实验以评估 Yelp 和 Amazon 数据集上欺诈检测任务的准确性。 我们报告了 RioGNN、基线和变体在 500 个 epoch 中的最佳测试结果。 从结果可以看出，在大多数训练比率或指标下，RioGNN 的表现优于其他基线和变体。 这表明 RioGNN 在欺诈检测场景中的可行性。

单一关系与多重关系 表 4 显示了针对欺诈检测任务建立在不同类型图上的基线实验结果。 为了解决实际细粒度应用中复杂网络的多样性和异构性，我们考虑引入具有多关系图结构而不是单一关系结构的神经网络。 但是，从表中一些基线的结果来看，虽然 GCN、GAT、GraphSAGE 和 GeniePath 模型在单一关系图上运行，但它们在 Yelp 数据集的准确性方面优于 RGCN、Player2Vec 和 SemiGNN，它们是在多关系图上运行。上面的观察表明，以前的多关系 GNN 不适合在欺诈检测任务中构建多关系图。 亚马逊数据集中出现了类似的现象。 此外，GraphConsis、FdGars、CARE-GNN 和 RioGNN 在 Yelp 和 Amazon 数据集上明显优于其他模型 8.60%-32.78%。 这是因为这四个模型在聚合之前根据节点特征对邻居进行采样，说明不纯邻居会干扰聚合过程，欺诈检测任务对邻居采样优化有强烈的需求。 与 GraphConsis 和 FdGars 的性能相比，CARE-GNN 和 RioGNN 将 AUC 提高了 3.51%-21.65%。这是因为 RioGNN 可以通过参数化相似度度量和自适应采样阈值更好地利用内部关系解决下游应用问题，这说明自动采样对欺诈检测任务有显着的改进效果。 更显着的结果是，所提出的RioGNN模型与CARE-GNN相比提高了5.90%和10.41%的准确率。 验证了标签感知邻居相似度度量与递归可扩展强化学习框架相结合的优势，可以有效突破CARE-GNN状态观察范围和手动指定策略的局限性。 同时，RioGNN 在欺诈检测任务上具有良好的效果。

异构与多重关系 为了进一步分析多关系图的准确性，我们在强化学习指导下的最新GNN模型上进行了异构图实验和多关系图实验。 从表4中异构图模型${\text{GraphNAS}}^H$、${\text{Policy-GNN}}^H$和多关系图模型GraphNAS和Policy-GNN的结果可以发现，多关系图与异构图相比在Yelp和Amazon数据集中为AUC带来了0.33%-1.71%的提升。这证实了在其他类似的模型中，我们构建的多关系图仍然具有明显的优势。 此外，我们发现同样基于强化学习指导并使用多关系图的GraphNAS和Policy-GNN在AUC和Recall上没有明显的优势。 这是因为 GraphNAS 和 Policy-GNN 不能自适应地采样不同的关系，这导致它们受到 Yelp 和 Amazon 数据集之间关系复杂性的限制。 而对于 Policy-GNN，由于 Yelp 和 Amazon 的单跳邻居信息已经足够丰富，更多的多跳策略并不能带来显着的收益。

训练百分比 为了衡量训练比率对分类准确度的影响，我们使用 5% 到 40% 的四种不同比率进行实验。从表 4 可以看出，大部分基线性能变化与训练百分比的增加并不一定相关。这表明利用少量监督信号的半监督学习方法足以训练一个好的模型。而且，在 Yelp 数据集的四种不同训练比例中，RioGNN 的 AUC 波动范围仅在 1.57% 以内，而 CARE-GNN 的 AUC 波动范围为 4.44%。在亚马逊，这两种模式都有很好的稳定性。这是因为 Amazon 节点特征提供了足够的信息来区分欺诈者，其质量高于 Yelp 数据集。从另一个结果也验证了RioGNN在复杂环境下具有更好的稳定性和适应性。

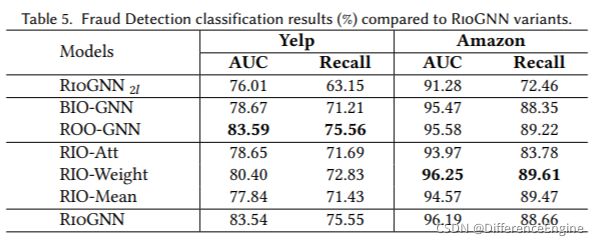
分类中的RioGNN变体 为了衡量新增机制对欺诈检测任务分类准确度的积极影响，我们比较了离散策略下的 RioGNN 的几种变体。 实验设置训练数据比例为40%，其他设置同4.1节。 我们展示了 Yelp 数据集中垃圾评论分类和亚马逊数据集中可疑用户分类的实验结果，如表 5 所示。从结果来看，所有变体的性能都优于基线模型。 接下来，我们将从三个方面讨论不同变体的影响。

首先，在两个数据集中，除了${\text{RioGNN}}_{2l}$变体，所有其他变体都仅使用具有一层结构的Label-aware Similarity Measure。 从表 5 中的结果来看，${\text{RioGNN}}_{2l}$变体低于所有其他变体，但它的表现优于所有基线。 可以发现，在欺诈检测任务中，层数的增加并没有带来分类准确率的显着提高。 这受限于 Yelp 和 Amazon 的数据集大小，并且在多跳邻居中信息的重要性较低。 我们将在第 5.1.3 节继续探索更多的多层效果。

其次，对于相似性感知邻居选择器部分，我们观察了没有自适应策略优化强化学习算法的变体BIO-GNN和没有RSRL框架的递归框架的单深度结构变体ROO-GNN的比较结果。 表 5 的第二部分给出了部分优化的证据。 BIO-GNN 变体在 RioGNN 模型上的结果表明，Yelp 和亚马逊中的自动策略优化有效提高了 4.65% 和 0.89% 的分类准确率，并且 BIO-GNN 变体也远优于大多数基线模型。 这说明马尔可夫决策过程对搜索聚合过程的过滤阈值有积极作用。而且，具有动态迭代函数和全动作空间学习过程的强化学习算法打破了固定策略和观察范围的限制，获得了更好的阈值选择效果，这也印证了3.2.2节的猜想。 此外，结合图8和表5，ROO-GNN变体的准确率与RioGNN相比几乎没有变化，即RioGNN的多深度结构可以比单深度变体ROO-GNN更快收敛，同时保持更高的准确率。这也意味着递归框架在分类精度方面的稳定性。

最后，从表5第三部分不同关系的聚合方法变化的结果来看，RioGNN在Yelp数据集上比其他三个有明显优势，RIO-Weight和RioGNN在Amazon数据集上都有不错的效果。证实了RioGNN不需要训练额外的注意力权重，使用过滤阈值作为相互关系聚合权重可以提高GNN的性能并降低模型的复杂度。因此，与其他变体相比，它可以获得最佳性能。 对于三个变体，RIO-Weight 的结果比其他两个都要好，但是 RioGNN 在不同质量和结构的数据集上可以保持更好的准确率，并且具有一定的适应性。

聚类中的RioGNN变体 为了探索 RioGNN 在聚类任务中的有效性，我们对 RioGNN 及其变体模型进行了聚类实验。 实验设置固定的训练率为 40%。 我们通过 K-Means 对 RioGNN 学习的节点表示进行聚类。 结果如表 6 所示。我们分别统计了 500 个 epoch 内 NMI 和 ARI 指标的最佳值。从结果可以看出，与${\text{RioGNN}}_{2l}$和BIO-GNN相比，RioGNN在Yelp数据集中的NMI和ARI指标分别至少提升了9.04%和10.33%。 同样，亚马逊数据集至少上涨了 2.39% 和 1.87%。这种现象与分类结果相同，受数据集大小的限制、动作空间的选择、动态迭代函数的影响。 此外，Yelp数据集中ROO-GNN的NMI和ARI取得了最好的结果，而Amazon数据集中的RioGNN则超过ROO-GNN的NMI和ARI3.45%和2.31%。 这是因为 Yelp 数据集比 Amazon 小，所以递归框架的优化空间也更小。 这表明递归框架在密集数据集上具有更好的优势。更值得注意的是RioGNN在聚类实验中的效果超过了所有GNN聚合变体的效果。 NMI和ARI在Yelp数据集中超过0.17%-3.83%和0.57%-7.65%，在Amazon数据集中超过2.5%-5.5%和1.67%-1.89%。 这说明直接使用过滤阈值作为聚合的权重在聚类任务中具有明显的优势。

5.1.2 可解释的RSRL训练过程。

本节重点介绍 RSRL 框架，并详细讨论强化学习过程的可解释性。 我们展示了在 Yelp 和 Amazon 数据集的训练过程中，RioGNN 过滤阈值和不同关系相似度得分的变化过程。 为了更好地比较，我们还对 ROO-GNN 和 BIO-GNN 变体进行了类似的分析。

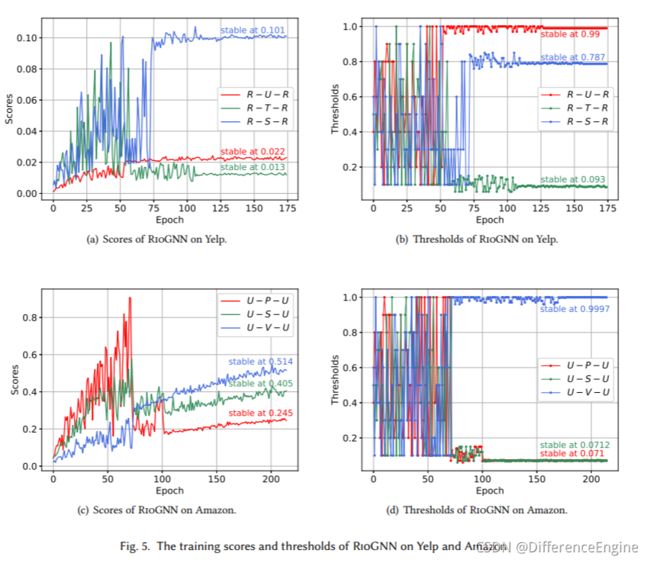
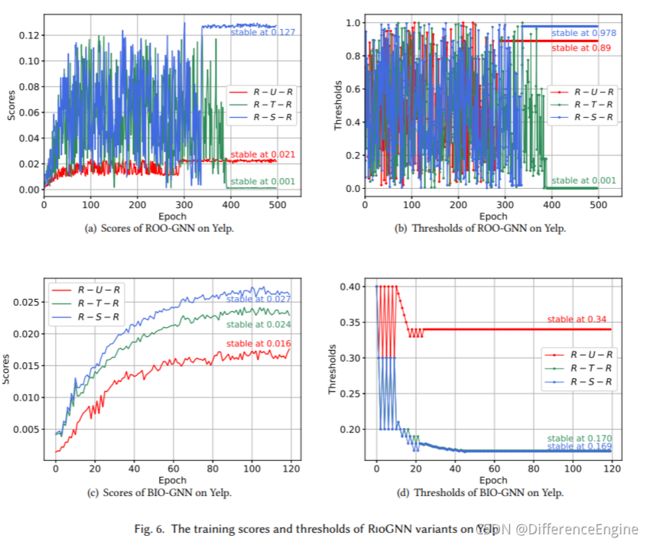
过滤阈值 在表 2 中，我们观察到 Yelp 和 Amazon 中大多数关系的平均特征相似度非常高。 但是，有一个关系如R-T-R，其标签相似度很低，为0.05，这表明欺诈者成功伪装了自己。 为此，我们建议通过过滤阈值过滤 Top-p 采样中排名较低的邻居。从图5(b)和图5©可以看出，Yelp数据集三个关系的过滤阈值稳定在[0.99,0.093,0.787]，Amazon数据集收敛到[0.071,0.0712, 0.9997]。 它表明不同关系的过滤阈值最终收敛到不同的值。原因是同一数据集中不同关系的标签相似度和特征相似度不同。 这一结果也可以从表 2 中得到验证。例如，R-U-R 和 R-T-R 之间的标签相似度差异为 0.85，而特征相似度差异仅为 0.04。 提出的框架为每个关系构建强化学习树，使用关系之间的相似性作为奖励，并独立找到合适的过滤阈值。 由于关系之间的相互影响，最终会得到一组纳什均衡过滤阈值，这是一种最能消除欺诈者干扰的抽样方案[16]。在纳什均衡中，所有智能体不可能仅通过改变自己的策略来获得更大的回报。 另外，在图5(b)和图6(b)、图6(d)中，我们还观察到在同一个数据集下使用了不同的模型，它们收敛并结合不同的过滤阈值[0.99,0.093,0.787 ],[0.89,0.001,0.978],[0.34,0.17,0.169] 分别。由于强化学习的结果是通过所有agent的连接策略得到的，每次关系之间的博弈达到纳什均衡时，可能会有很多不同的过滤阈值组合[37, 79]。

图 5(a) 和图 5(c)展示了不同关系在过滤阈值学习过程中获得的奖励变化。我们观察到在Yelp数据集中，R-S-R和R-U-R关系在三者的利益竞争中实现了更好的回报增长。相反，R-T-R关系最终稳定在一个相对较低的奖励。这与实际场景是一致的。同一产品中具有相同星级的评论是划分垃圾评论的重要考虑因素，同一用户的评论通常具有相同的趋势。然而，在同一个月发表的评论的影响因子较低。相似Amazon数据集的U-P-U和U-S-U比U-V-U关系更有意义。这意味着发布相似内容的用户联系更紧密，被认为是用户判断的重要观察因素。

递归的框架 在图 6 的右栏中，我们展示了 ROO-GNN 和 BIO-GNN 两种变体在 Yelp 数据集上的过滤阈值变化。 比较图5(b)中的RioGNN和图6(b)中的ROO-GNN，可以看出RioGNN采用图5(b)的递归框架对每个深度进行了更准确的过滤阈值搜索。例如，首先在区间[0,1]中以0.1的精度探索关系R-U-R，获得0.9的收敛性。 然后寻找[0.85,0.95]之间的收敛，得到关系R-U-R的最高精度0.01，并得到最终收敛0.99。 与RioGNN不同的是图6(b)中的ROO-GNN模型，其中只进行了一次深度强化学习。比如R-U-R直接探索[0,1]区间，精度最高0.01，得到最终收敛值0.89。 除了上面提到的不同，我们还可以看到是否存在图 5(a) 和图 6(a) 所示的递归奖励变化。 对于有递归的RioGNN，所有关系在110个epochs完全收敛，而没有递归的ROO-GNN在390个epochs收敛。 此外，两种方法获得的奖励基本相同。这解决了我们在2.2节中提出的挑战，并解释了减少每个强化学习的动作数量可以有效地加速模型的收敛。实验结果还表明，加入递归不会带来明显的精度损失，这是显著的。

动作空间和迭代函数 在图5(b)和图6(d)中，我们给出了具有动态迭代函数和全动作空间学习过程的BIO-GNN变体和RioGNN。可以看出，与RioGNN相似，BIO-GNN对于R-U-R关系也递归收敛到0.4，精度为0.1，然后收敛到0.33，精度为0.01。但与RioGNN不同的是，该方法对于三个关系的平均相似度得分为0.045，低于RioGNN的0.021。 这意味着还没有达到最大的过滤效果。 在其他方面，与图 5(a) 和图 6(a) 获得了更好的性能相比，图 6(c) 的 R-T-R 关系在竞争中获得了更高的奖励比率。即BIO-GNN认为同月发表的行为更重要，这与实际情况相反。这就解释了BIO-GNN性能较低的原因。

同时，这些结果表明，动态学习可以全局观察，从而获得更多的效果，这也证明了第3.2.2节的猜想。

5.1.3 效果和效率评价。

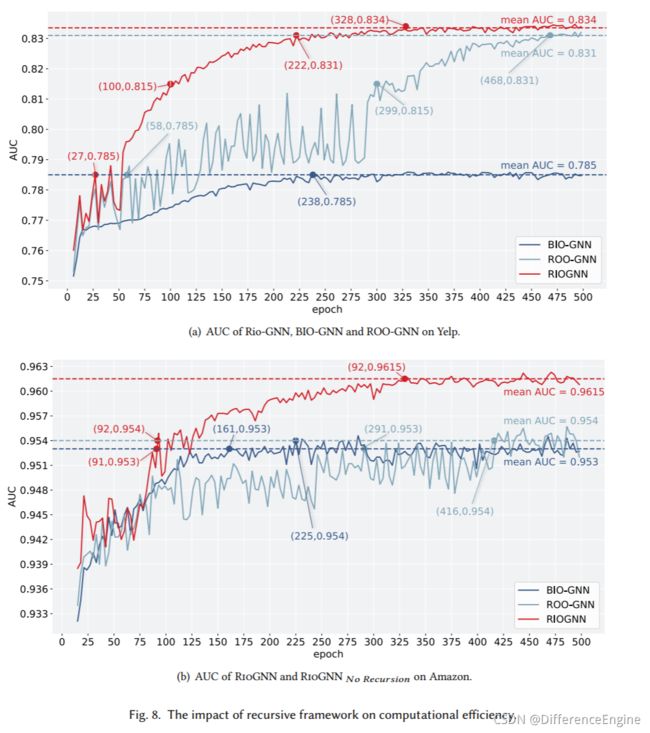
接下来，我们介绍了多层相似性感知模块和递归邻居选择器在两个数据集上的欺诈检测任务中的有效性和效率。 我们使用具有两层感知结构的RioGNN在Yelp数据集上训练500个epochs，选取前250个epochs来展示图7中每层分数的变化。对于递归框架，我们分析了ROO-GNN的AUC变化趋势， BIO-GNN 变体和 RioGNN 在 500 个 epoch 内的两个数据集（图 8）。 图中虚线表示每个变体达到稳定后的平均AUC。 图中特别标注的点表示不同模型达到某个AUC的epoch数。

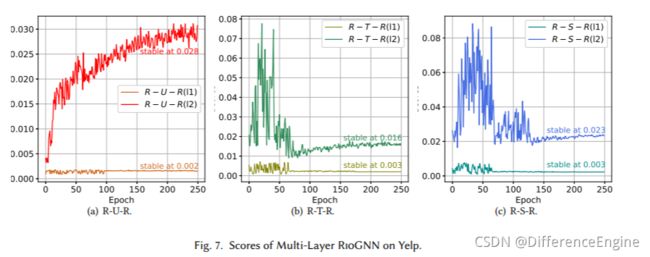
多层分析 我们提供了一个多层标签感知的相似性邻居测量方案，以处理未来具有更复杂结构的数据集合。 对于本文中的数据集，多层的增加受到数据集的限制（一跳邻居信息足以采样），其带来的AUC增益是有限的。然而，我们在图 7 中注意到，随着层数的增加，与 Layer1 相比，Layer2 在每个关系的相似度得分上都有显着提高。 其中，关系R-U-R在第二层与第一层的相似度得分为14.00。 此外，R-T-R 和 R-S-R 在 5.33 和 7.66 中都有改进。这是因为我们把前一层邻居的嵌入作为第二层的输入，嵌入更多的邻居关系的跳数。丰富的邻居信息使得相似度模块的性能更好。这也说明，在单跳邻居嵌入信息不足的数据集中，多层连接是一种新的部署方案。

多深度分析 为了在保证准确率的同时有效加快每个关系过滤阈值的优化速度，我们提出了一种递归强化学习框架。 从图 8 可以看出，RioGNN 模型在两个数据集中都比 ROO-GNN 和 BIO-GNN 具有明显的优势。 首先，我们观察最终收敛的 AUC 大小。 在 Yelp 数据集中，RioGNN 和 BIO-GNN 模型比 ROO-GNN 高约 4.75%。在 Amazon 数据集中，RioGNN 比其他两个模型好 0.8% 左右。 而且BIO-GNN最终收敛的AUC普遍偏低。 此外，在计算效率方面，与没有递归的ROO-GNN模型相比，RioGNN在两个数据集中都保持了AUC的稳定快速增长。但是，ROO-GNN 有较大的波动。 在 Yelp 的前 50 个 epoch 和 Amazon 的前 75 个 epoch 中，它们之间没有显着差异。 在 Yelp 数据集中，RioGNN 与 ROO-GNN 相比，AUC 达到 78.5% 时的加速比为 2.14，AUC 达到 81.5 时为 2.99，AUC 达到 83.1% 时为 2.10。在 Amazon数据集中，AUC达到95.30%时加速比为3.19，AUC达到95.4%时加速比为4.52。 与有限动作空间和固定策略的 BIO-GNN 相比，Yelp 和 Amazon 在 78.5% 和 95.3% 的 AUC 上也观察到了 8.81 和 1.71 倍的时间节省。 这表明所提出的递归框架可以在保持准确性的同时实现良好的效率。 而且一般来说，AUC 需求越高，效率就越高。更广阔灵活的动作空间和自动更新的迭代函数在效率和准确性方面具有更显着的优势。最后，我们发现不同的优化结构对不同的数据集有不同的影响因子。由于Yelp数据集规模较小，精度要求较低，是否具有递归结构对最终收敛AUC影响不大。但在规模更大、精度要求更高的Amazon数据集中，将所有动作放在一个深度会导致精度损失。 这也印证了3.2.2节关于动作空间过大导致精度损失的猜想，印证了递归结构在大规模数据集中的优势。

5.2 糖尿病诊断任务的综合评价

5.2.1 准确性分析

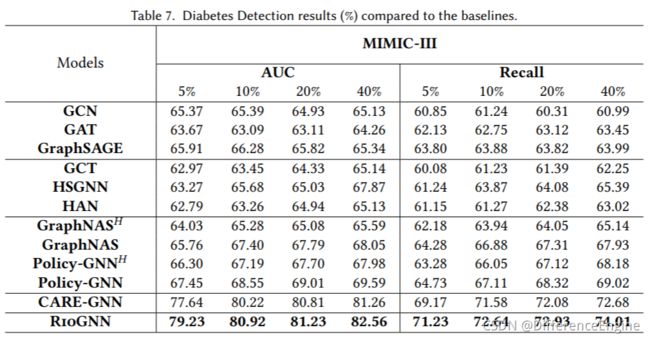
在本节中，我们进行实验以评估 MIMIC-III 数据集上糖尿病诊断的准确性。 如表 7 所示，我们报告了 RioGNN 和各种基线和变体在 700 个 epoch 中的最佳测试结果。 从结果可以看出，在大多数训练比率和指标下，RioGNN 的表现优于其他基线和变体。

单一关系与多重关系 为了进一步证明 RioGNN 在处理多关系图方面的有效性，我们对更具挑战性的糖尿病诊断任务进行了基线比较。 表 7 显示了 RioGNN 和三种基线的比较结果。 与在单关系图上运行的第一类基线：GCN、GAT 和 GraphSAGE 相比，模型RioGNN 在 MIMIC-III 数据集上明显优于它们 13.32%-18.30%。这一结果充分证实了多关系图的细粒度划分和基于不同关系的层次聚合非常有利于节点分类任务的完成。 这一点与欺诈检测任务的实验结论完全一致。 此外，为了展示RioGNN在处理多关系图时的性能，我们进行了第二种基线对比实验。尽管 GCT、HSGNN 和 HAN 都运行在异构图上，并提出了不同的处理异构关系的思路，但它们的准确率至少比 RioGNN 低 8.77%。 由于每个关系下的邻居节点密度高，无法有效过滤干扰节点也给最终的诊断任务带来困难。与RioGNN相比，很明显它们未能滤除干扰邻居节点，对最终诊断产生足够强的正面影响。 有趣的是，比较两种基线，我们发现虽然第二种基线在一定程度上划分了异构关系，但它们在大多数情况下甚至比在单关系图上运行的第一种基线更差。 以上结果表明，在处理多关系图时，如何有效地选择合适的邻居节点尤为重要，而RioGNn通过参数化的相似性度量和自适应采样阈值很好地实现了这一点。当涉及到第三种基线 CARE-GNN 时，我们发现它的准确率明显高于前两种基线 11.73%-17.70%，这意味着异构图的细粒度和多关系划分 非常有必要。 CARE-GNN虽然在一定程度上实现了邻居节点的自动过滤和采样，但由于无法自适应地选择每个关系下的最佳过滤阈值，其诊断效果低于RioGNN。 以上表明，所提出的RSRL框架在递归过程中成功地找到了每个关系下的最佳过滤阈值，因此在下游任务中表现出色。

异构与多重关系 与欺诈检测任务同步，我们还分析了 GraphNAS 和 Policy-GNN 模型在异构图和多关系图中在疾病检测任务中的性能。 从表 7 可以得到与欺诈检测任务相同的现象，即在 Mimic 数据集上引入多重关系图与异构图相比也具有一定的优势。 但是，与 Yelp 和 Amazon 不同，GraphNAS 和 Policy-GNN 在准确性方面通常优于其他基线。 我们认为原因在于具有不同关系的 Mimic 数据集的平衡特征和标签，以及大规模数据集对邻居信息的更高聚合要求。

训练百分比 为了衡量训练比率对糖尿病诊断任务中分类准确率的影响，我们仍然设置了 5% 到 40% 的四种不同的训练比率。 从表 7 可以看出，随着训练比例的增加，RioGNN 的分类准确率呈现稳步上升的趋势。 这说明RioGNN的训练过程对最终的分类准确率有着非常积极的影响。直观上可以看出，RioGNN在监督信号的强化学习递归过程中成功取得了不错的性能提升，也符合预期。 然而，一些基线的准确率变化与训练百分比无关，这意味着他们的训练方法在这个任务上有很大的局限性，无法通过增加有监督的信号学习过程来提高他们的模型的性能。也验证了RioGNN具有更好的可解释性，可以通过学习更多的节点特征，不断提高诊断的准确率。 与其在之前的欺诈检测任务下的表现一致，RioGNN 仍然保持着很强的稳定性和可解释性，其准确率在每个训练比率上都超过了其他人。

聚类中的RioGNN变体。

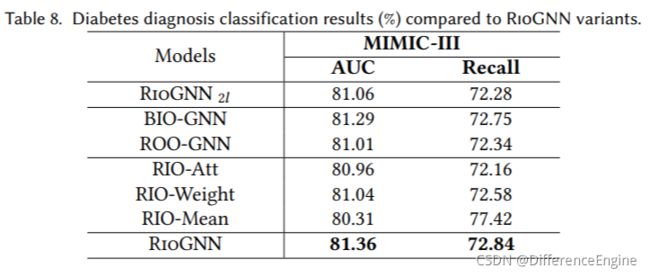
为了进一步验证所提出的新机制对不同任务的影响，我们在糖尿病诊断的背景下比较了离散策略下RioGNN的几种变体的不同性能。 我们在表 8 中展示了在 MIMIC-III 数据集上诊断糖尿病的实验结果。首先，我们在 MIMIC-III 数据集上比较了基于不同聚合方法的三种变体。结果表明，RioGNN 优于其他三个变体，而 RIO-Weight 的结果优于其他两个，这与 Yelp 数据集上的结果一致。 我们发现聚合方法的选择通常基于特定的数据集。 对于不同的数据集，不同的关系对结果的影响方式也不同，这就导致了不同的聚合方法。 但是，无论是针对 Yelp、Amazon 还是 MIMIC-III，结果都表明 RioGNN 优于所有聚合变体，而 RIO-Weight 仅次于。这一点具有一定的普遍性。 接下来，我们还关注具有两层结构的RioGNN变体${\text{RioGNN}}_{2l}$的性能。 与之前在 Yelp 和 Amazon 上的结果一致，两层架构并没有给 MIMICIII 上的模型带来非常好的性能提升。 与RioGNN相比，可以发现层数的增加并没有提高最终的准确率，说明使用基于标签感知相似度度量的单层结构进行邻居选择是最优的。但是，结合表 2 可以看出，MIMIC-III 数据集比 Yelp 和 Amazon 更密集，${\text{RioGNN}}_{2l}$ 的效果非常接近 RioGNN。 这表明对于更密集的关系，${\text{RioGNN}}_{2l}$ 找到的二阶邻居在最终结果中更有效。 在某种程度上，对于过于密集的多关系图，二阶邻居可以作为一阶邻居的补充信息。最后，对于标签感知相似性度量部分，我们再次在MIMIC-III上观察了没有自适应策略优化强化学习算法的变体BIO-GNN和没有RSRL框架递归框架的单深度结构变体ROO-GNN。 从表 8 和表 7 可以发现，ROO-GNN 的性能明显优于大多数基线和变体，仅次于 RioGNN。这说明离散策略的伯努利多臂老虎机(BMAB)算法在递归选择关系过滤阈值的过程中具有很强的适应性。 相比之下，ROO-GNN 的准确率比 BIO-GNN 低 0.28%。 除此之外，图10显示，随着训练epoch的增加，ROO-GNN在79.48%-81.43%的范围内波动很大，并且永远不会像RioGNN或BIO-GNN那样在固定的较小区间内保持稳定。也就是说，RioGNN的多深度结构比单深度变型ROO-GNN具有更好的收敛速度和良好的稳定性，同时保持了较高的准确率。

聚类中的RioGNN变体 与欺诈检测类似，我们也在疾病诊断任务中进行聚类分析。 700个epochs内NMI和ARI的最佳结果记录在表9中。可以看出，与BIO-GNN和ROO-GNN相比，RioGNN分别带来了至少0.29%和1.76%的NMI和ARI增加。 这证明了 RSRL 框架也为聚类任务中的密集数据集带来了精度优化。此外，对于使用不同聚合方法的变体，RioGNN 在 ARI 指标上有更好的表现。 对于 NMI 指标，RIO-Weight 效果已得到改进。 我们认为这是因为与 Yelp 和 Amazon 相比，MIMIC-III 数据集在关系之间的权重差异较小。 权重可以比RioGNN更好地区分不同的类别，RioGNN直接使用过滤阈值作为聚合参数。

5.2.2 可解释的RSRL训练过程。

本节重点介绍强化学习的过程，并解释了拟议的RioGNN在MIMIC-III数据集上的收敛过程。 我们还对不同变体进行了比较分析，以进一步解释 RioGNN 的适用性。

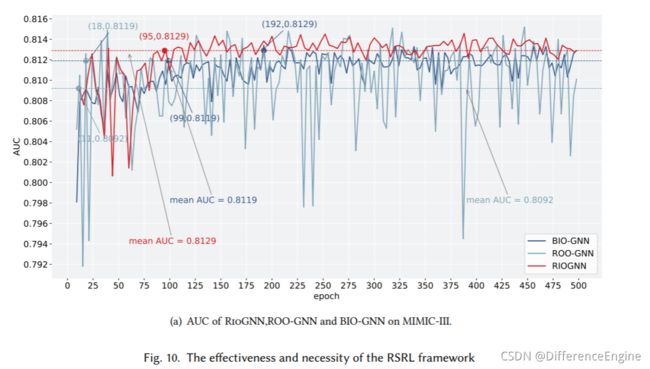
**RSRL 框架的有效性和必要性。**这部分通过比较 RioGNN 与变体及其初步版本 CARE-GNN 来证明所提出框架的有效性和必要性。 从图 10 可以看出，RioGNN 几乎在每个 epoch 中的表现都优于 CARE-GNN，这证明 RSRL 框架对 MIMIC-III 上的最终分类结果有积极影响。 每个关系并更准确地识别可疑节点。与RioGNN相比，图9中ROO-GNN的准确率波动较大，难以收敛到一个稳定的范围，证明了建立递归过程的必要性。 通过RSRL过程，分类精度可以保持在一个相对稳定的范围内。 实验结果表明，通过对每个深度进行更准确的过滤阈值搜索，具有递归框架的RioGNN表现更好。 而没有递归的 ROO-GNN 不仅无法在有限数量的 epoch 内收敛，而且会导致精度损失。

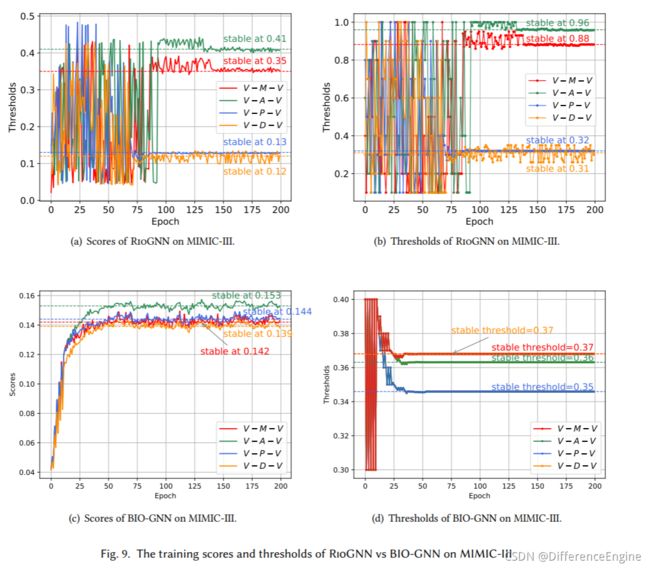
过滤阈值 为了进一步测试所提出模型对可疑邻居的过滤性能，我们在设计 MIMIC-III 数据集时特意提取了四个更密集的关系。 每个关系至少比 Yelp 或 Amazon 数据集高一个数量级，这意味着 MIMIC-III 数据集对于 RioGNN 的过滤性能更具挑战性。从图9(b)和图9(d)可以看出，RioGNN在MIMIC-III数据集上的四种关系的过滤阈值稳定在[0.88,0.96,0.32,0.26]，而BIO-GNN稳定在 [0.35, 0.37, 0.36, 0.37]。考虑到不同关系的标签相似度和特征相似度不同，模型对不同关系的过滤强度也不一样。 值得注意的是，RioGNN 和 BIO-GNN 上的关系过滤强度有一定的共性。 在 RioGNN 下，V-A-V 和 V-M-V 的收敛阈值比较相似，而 V-P-V 和 V-D-V 的收敛阈值比较相似。 一般来说，高过滤阈值的关系可以给诊断结果带来更积极的指导，也更容易解释。从另一个角度来看，较高的过滤阈值可以证明所选关系的可解释性和正确性，更有利于我们直观地判断关系的选择是否足够合适。从图 9 中可以明显看出，RioGNN 的这四个关系在 100 个 epoch 内收敛到一个稳定值。 这表明该算法可以通过RSRL框架在非常有限的epoch内获得一组Nash均衡滤波器阈值，因此具有良好的稳定性和较高的效率。

5.3 RSRL框架的通用性分析

为了更好地适应许多任务驱动的场景，我们实现了一个通用的 RSRL 强化学习框架。 在处理不同大小和类型的数据集时，可以灵活匹配不同的强化学习算法和动作空间类型。 可以为每个关系自适应地估计强化学习树的深度和宽度。

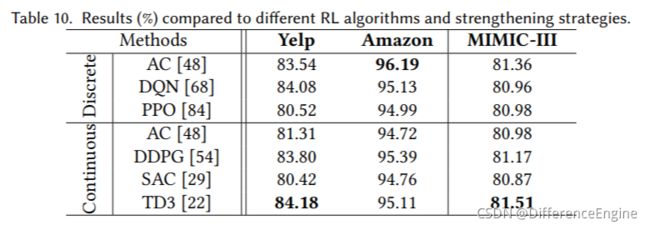
不同任务场景的算法和动作空间 在表 5 中，为了讨论一些函数变体的比较，我们固定使用经典的强化学习算法 Actor-Critic 进行实验。这里，为了更好地探索RioGNN对于不同强化学习算法的通用性以及强化学习算法对不同任务的适用性，在表10中我们选取了当前主流的强化学习算法进行实验，并记录了500个epoch内的最佳AUC值。 此外，对于RSRL框架，我们在3.2.2节中提出了两种不同的动作空间用于构建强化学习森林，以适应不同的任务需求。与离散动作空间不同，具有连续动作空间的强化学习框架在强化学习的每一个动作选择中都具有连续精度（即处理器的最高浮点数）。 这种差异使其在大规模数据集中具有更好的探索效果。 从实验结果来看，PD3算法连续动作空间和两组网络更新Q值在Yelp和MIMIC-III数据集上都取得了最好的效果。在 Amazon 数据集中，最好的结果是从更基本的离散动作空间 AC 中获得的。 SAC 和 PPO 在三个数据集中都处于较低水平。 总的来说，RioGNN 很好地适应了大多数强化学习算法，是一个适用于不同类型数据集和任务场景的通用框架。

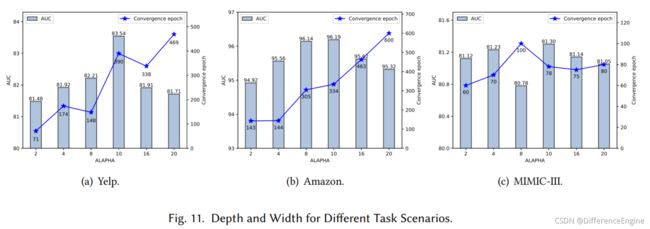
不同任务场景的深度和宽度 在3.2.2节中，我们定义了一个深度和宽度自适应参数$\alpha$来调整关系的每一层的动作空间的大小和整个关系树的深度。 在之前的实验中，我们固定选择了 10 作为$\alpha$。在本节中，为了讨论深度和宽度自适应参数对 RioGNN 模型的准确性和效率的影响，我们比较和分析了三个数据集在不同设置下的 AUC 和收敛时期大小。 如图11所示，我们设置了2、4、8、10、16、20这6个$\alpha$值，分别记录了500epochs中得到的最大AUC和对应的epoch序号。在Yelp数据集中，AUC在$\alpha$为10时达到最大值，至少比其他参数好1.33%。 但在这种情况下，达到这个值需要更长的时间。 因此，我们建议 Yelp 可以自适应地选择$\alpha$为 8 或 10，以实现效率优先和准确性优先。 另一方面，Amazon数据集在$\alpha$为 8 或 10 时实现了更好的准确率，而在$\alpha$为 2 或 4 时实现了更好的效率。与前两者不同的是，MIMIC-III数据集在$\alpha$为8时获得了精度和效率的损失。从这些情况来看，RioGNN可以通过调整$\alpha$来适应不同规模和不同精度和效率偏差的数据集。 这代表了数据集大小和任务要求的多功能性。

5.4 归纳学习分析

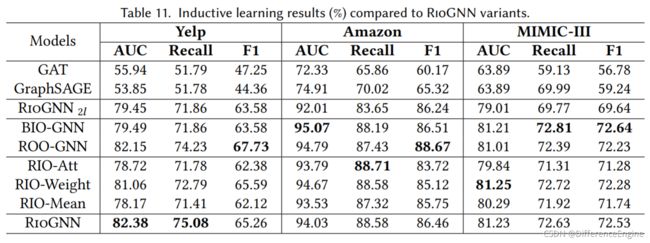
在本节中，我们对 RioGNN 进行归纳学习，RioGNN 的一些代表性基线和变体模型。 在前面的实验中，我们使用了转导学习，即传入模型的图包含测试节点。 在归纳学习中，我们只将需要训练的节点的邻接矩阵传入模型，并记录Yelp和Amazon在500个epoch内和MIMIC-III在700个epoch内的最佳AUC、Recall和F1指标。从表11的结果可以看出，RioGNN相比GAT和GraphSAGE仍然具有明显的优势，其中AUC、Recall和F1提升了17.34%-28.53%、2.64%-23.30%、13.29%-20.90%。此外，RioGNN 在众多变体中具有相对稳定的评价指标。 其中，Yelp数据集上的结果与转导学习的结果对比见表5。 在归纳学习中，RioGNN的AUC和召回率不断超过ROO-GNN变体，尽管RioGNN在转导学习中略低于ROO-GNN 表 11。这代表了递归框架在具有挑战性的任务中性能的稳定性，并说明了其在小规模场景中的优势。 在亚马逊数据集中，由于数据规模的扩大，一些变体在某些方面得到了较好的评价，但从AUC、Recall和F1的综合情况来看，RioGNN稳定在较高水平。 这种情况同样出现在 MIMIC-III 中。值得注意的是，与它们在转导学习任务中的情况相比，Amazon 和 MIMIC-III 数据集中的 BIO-GNN 变体实现了良好的性能提升。 我们认为这是因为与 演员-评论家相比，BMAB 的学习能力相对较弱，降低了学习模型对训练集的依赖，因此更兼容新增节点。 总的来说，RioGNN在转导学习和归纳学习中都有很好的适用性。

5.5 超参数灵敏度

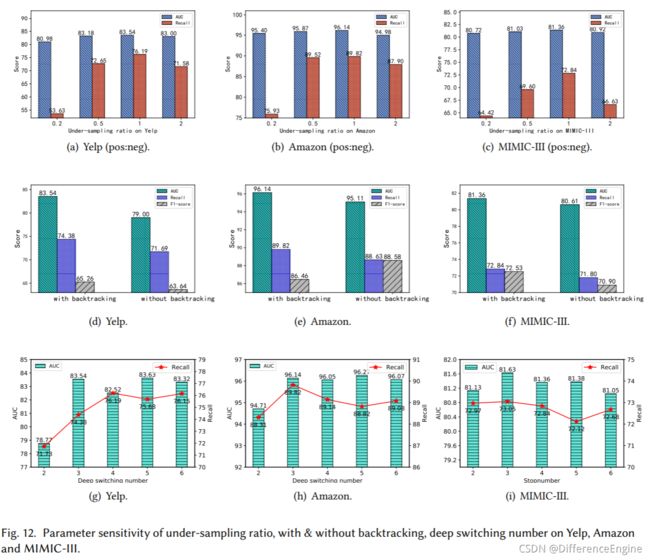
图 12 显示了我们在 4.4 节中介绍的三个超参数在三个数据集上的测试性能。 图12第一行显示了RioGNN训练集在不同采样率下的AUC和Recall（注意测试结果来自不平衡的测试集）。 可以看出，当采样率为1:0.2时，即负样本远小于正样本时，三个数据集都出现过拟合。与1:0.5和1:2采样率相比，1:1采样在所有三个数据集中显示出更高的AUC和Recall指标。 图 12 的第二行研究了我们在 3.2.2 节中设置的回溯结构。 从图 12(d)、图 12(e) 和图 12(f) 中，与没有回溯的模型相比，具有回溯设置的模型在所有数据集中都带来了稳定的性能。 在图 12 的第三行，我们测试了不同的深度切换条件。 当深度切换次数设置为 3 时，AUC 和 Recall 实现了良好且均衡的性能。

六、相关工作

在过去的几年中，图神经网络（GNN）和强化学习（RL）技术受到越来越多的关注，并提出了许多升级算法。 因此，现有文献可以大致分为三类：半监督图神经网络、RL 和 RL 引导的 GNN。

6.1 半监督图神经网络

根据对现实世界图数据建模的差异，我们将半监督图神经网络方法大致分为同构图神经网络、异构图神经网络和多图学习模型。

同构图神经网络 它们通常是指那些不考虑节点的数据类型或图上边的属性的 GNN 方法。 经典方法包括 GCN [47]、Graph-SAGE [30] 和 GAT [94]。 如上一节所述，GCN 模型定义了第一个成功的图卷积，类似于欧几里德数据上的卷积层，因此被视为非网格拓扑的卷积神经网络 (CNN) 的泛化。Graph-SAGE 模型利用采样为每个节点获取固定数量的邻居，以通过聚合函数生成节点嵌入，如果应用了节点排序的排列，例如均值、总和或最大值函数，则该聚合函数可以保持不变。 此外，Graph-SAGE 模型提出了第一个通用归纳学习框架，该框架不断采样和聚合其本地邻居的特征，以生成新节点的嵌入。相比之下，GAT 模型首先采用注意力机制来学习两个连接节点之间的相对权重。 进一步加强多头自注意力以提高模型的表达能力。 尽管这些模型具有强大的图表示学习能力，但主要的限制是对现实世界数据和应用程序中表现出的数据类型和关系的多样性的无知。

异构图神经网络 在通过神经网络从节点的本地邻居聚合特征信息时，这种方法通常会考虑节点类型或边缘类型的异质性。 经典的基于元路径和元图的方法包括 GAS [51]、HAN [100]、Player2Vec [117]、HSGNN [61] 和 MAGNN [21]。 考虑到现实世界数据中边的多样性，开发了更多关系图神经网络方法，包括 R-GCN [83]、SemiGNN [97]、FdGars [98] 和 GraphConsis [60]。 其他异构图神经网络，包括 HGT [38]、GEM [59]、HetSANN [35] 等，在异构邻居之间实现复杂的神经聚合。所有这些异构模型都是以前的异构模型的升级版本。 然而，没有文献探讨如何选择邻居节点来构建最具表现力、解释性和稳定的聚合。

多重图的学习模式 除了上述解决单图表示学习的同构和异构 GNN 之外，多图神经网络模型 [64,65,86,101,116] 研究融合多个特征来综合学习图数据对象的嵌入。 MGAT [104] 探索了从每个单一视图学习节点表示的基于注意力的架构和以视图为中心的注意力方法来聚合视图节点表示。多视图知识图嵌入 [114] 是通过使用跨视图实体身份推理来捕获两个知识图之间的对齐信息来呈现的。 为了过滤掉无用的特征交互，在推荐任务中根据贝叶斯变量选择（BVS）理论设计了贝叶斯个性化特征交互选择机制[8]。 此外，提出了块对角正则化 [9] 来指导 top-N 推荐任务中的项目相似性。

6.2 强化学习

随着技术的发展，强化学习算法衍生出许多不同的发展方向。 更基本的算法是仅基于值的 Q-Learning [102] 和 DQN [68] 算法，它们使用值函数来估计和减少局部最优情况的发生。 然而，PPO[84]等基于策略的算法直接对策略进行迭代计算，可以实现更好的收敛。Actor-Critic 类型的强化学习方法 AC [48]、DDPG [54]、TD3 [22] 和 SAC [34] 结合了基于价值和基于策略的优点，同时训练 Q 函数和策略 . 除了上述划分方法，从动作空间类型来看，DQN和Q-learning适合离散动作空间，DDPG、TD3、SAC支持连续动作空间，而PPO和AC既适合离散动作空间也适合连续动作空间行动空间。或者从学习方法来看，DDPG、DQN、SAC、TD3等强化学习算法结合深度学习，利用神经网络的拟合能力，获得更好的优化。 这些不同的算法具有不同的优势，但也带来了不同的局限性。 例如，仅支持离散动作空间的算法无法满足连续动作空间的要求，Actor-Critic 类型的算法在吸收了基于值的方法和基于策略的方法的同时继承了理想的缺点。 仅支持相同强化学习算法的框架在对多种类型任务的适应性方面存在局限性。

6.3 GNN与强化学习的结合

有一些尝试将 GNN 和 RL 结合起来。 DGN+GNN [2] 是一种用于概括未知网络拓扑的模型，其中对网络环境建模的 GNN 允许 DRL 代理在不同的网络上运行。 G2S+BERT+RL [11] 是一种用于自然问题生成的基于 RL 的图到序列模型，其中答案信息被有效的深度对齐网络利用，并且提出了一种新颖的双向 GNN 来处理有向通道图。同样，其他工作 [32,39,88] 研究了如何使用 GNN 来提高 RL 的泛化能力。 还有许多研究利用 RL 来优化图上的表示学习。 例如，DeepPath [105] 一个基于策略RL 的知识图嵌入和推理框架； 训练 RL 代理以确定知识库中的推理路径。 RL-HGNN [120] 为 HIN 中的任何节点设计不同的元路径以学习其有效表示。 它通过使用基于 DRL 的策略网络进行自适应元路径选择，将元路径设计过程建模为马尔可夫决策过程。与 RioGNN 不同，RL-HGNN 模型更注重揭示异构图分析中有意义的元路径或关系。 GraphNAS [23] 采用涵盖采样函数、聚合函数和门控函数的搜索空间，并使用 RL 搜索图神经架构。 Policy-GNN [49] 将 GNN 训练问题表述为马尔可夫决策过程，并且可以自适应地学习聚合策略以对不同节点的聚合迭代进行采样。 然而，GraphNAS 和 Policy-GNN 模型都没有考虑聚合中的异构邻域，尽管它们更关注神经架构搜索。

七、结论和未来工作

本文研究了RioGNN，一种增强的、递归的和灵活的邻域选择引导的多关系图神经网络架构，以学习更具辨别力的节点嵌入，并分别响应垃圾邮件评论检测和疾病诊断任务中不同关系重要性的解释。 RioGNN 分别使用强化学习技术设计了标签感知神经相似性邻居度量和强化关系感知邻居选择器。为了优化强化邻居选择的计算效率，我们进一步设计了一个递归和可扩展的框架，具有可估计不同尺度的多关系图的深度和宽度。 在三个真实世界基准数据集上进行的实验表明，RioGNN 在所有数据集上显着、一致且稳定地优于最先进的替代方案。 我们的工作显示了学习 GNN 的增强邻域聚合的前景，可能为未来的研究开辟新的途径，通过自适应邻域选择来提高 GNN 的性能，并分析不同关系在消息传递中的重要性。

未来，我们的目标是采用多智能体 RL 算法，进一步使 RioGNN 能够自适应地识别每个节点的有意义的关系，而不是手动定义关系，以实现异构数据的自动表示学习。 此外，研究如何将我们的模型扩展到图数据分析和应用的其他任务也很有趣，例如个性化推荐系统、社交网络分析等。

参考文献

[1]Aisha Abdallah, Mohd Aizaini Maarof, and Anazida Zainal. 2016. Fraud detection system: A survey.Journal of Network and Computer Applications68 (2016), 90–113.

[2]Paul Almasan, José Suárez-Varela, Arnau Badia-Sampera, Krzysztof Rusek, Pere Barlet-Ros, and Albert Cabellos-Aparicio. 2019. Deep reinforcement learning meets graph neural networks: Exploring a routing optimization use case.arXiv preprint arXiv:1910.07421(2019).

[3]Victor Bapst, Thomas Keck, A Grabska-Barwińska, Craig Donner, Ekin Dogus Cubuk, Samuel S Schoenholz, Annette Obika, Alexander WR Nelson, Trevor Back, Demis Hassabis, et al.2020. Unveiling the predictive power of static structure in glassy systems.Nature Physics16, 4 (2020), 448–454.

[4]Smriti Bhagat, Graham Cormode, and S Muthukrishnan. 2011. Node classification in social networks. InSocial network data analytics. Springer, 115–148.

[5]Bokai Cao, Mia Mao, Siim Viidu, and Philip S. Yu. 2017. HitFraud: a broad learning approach for collective fraud detection in heterogeneous information networks. InProceedings of the IEEE ICDM. 769–774.

[6]Yuwei Cao, Hao Peng, and Philip S. Yu. 2020. Multi-information Source HIN for Medical Concept Embedding. InProceedings of the PAKDD. Springer, 396–408.

[7]Hao Chen, Yue Xu, Feiran Huang, Zengde Deng, Wenbing Huang, Senzhang Wang, Peng He, and Zhoujun Li. 2020. Label-Aware Graph Convolutional Networks. InProceedings of the CIKM. ACM, 1977–1980.

[8]Yifan Chen, Pengjie Ren, Yang Wang, and Maarten de Rijke. 2019. Bayesian Personalized Feature Interaction Selection for Factorization Machines. InProceedings of ACM SIGIR. 665–674.

[9]Yifan Chen, Yang Wang, Xiang Zhao, Jie Zou, and Maarten De Rijke. 2020. Block-Aware Item Similarity Models for Top-N Recommendation.ACM Transactions on Information Systems38, 4, Article 42 (2020), 26 pages.

[10]Yu Chen, Lingfei Wu, and Mohammed J Zaki. 2019. Deep iterative and adaptive learning for graph neural networks.arXiv preprint arXiv:1912.07832(2019).

[11]Yu Chen, Lingfei Wu, and Mohammed J Zaki. 2019. Reinforcement Learning Based Graph-to-Sequence Model for Natural Question Generation. InProceedings of the ICLR.

[12]Wei-Lin Chiang, Xuanqing Liu, Si Si, Yang Li, Samy Bengio, and Cho-Jui Hsieh. 2019. Cluster-GCN: An efficient algorithm for training deep and large graph convolutional networks. InProceedings of the SIGKDD. ACM, 257–266.

[13]Edward Choi, Zhen Xu, Yujia Li, Michael Dusenberry, Gerardo Flores, Emily Xue, and Andrew Dai. 2020. Learning the graphical structure of electronic health records with graph convolutional transformer. InProceedings of the AAAI, Vol. 34. 606–613.

[14]Yingtong Dou. 2019. A review of recent advance in online spam detection. (2019).

[15]Yingtong Dou, Zhiwei Liu, Li Sun, Yutong Deng, Hao Peng, and Philip S. Yu. 2020. Enhancing Graph Neural Network-based Fraud
Detectors against Camouflaged Fraudsters. InProceedings of the CIKM. ACM, 315–324.

[16]Yingtong Dou, Guixiang Ma, Philip S. Yu, and Sihong Xie. 2020. Robust Spammer Detection by Nash Reinforcement Learning. In Proceedings of the KDD. ACM, 924–933.

[17]Gabriel Dulac-Arnold, Richard Evans, Hado van Hasselt, Peter Sunehag, Timothy Lillicrap, Jonathan Hunt, Timothy Mann, Theophane Weber, Thomas Degris, and Ben Coppin. 2016. Deep Reinforcement Learning in Large Discrete Action Spaces. arXiv:1512.07679 [cs.AI]

[18]David K Duvenaud, Dougal Maclaurin, Jorge Iparraguirre, Rafael Bombarell, Timothy Hirzel, Alán Aspuru-Guzik, and Ryan P Adams. 2015. Convolutional networks on graphs for learning molecular fingerprints. InProceedings of the NIPS. 2224–2232.

[19]Wenqi Fan, Yao Ma, Qing Li, Yuan He, Eric Zhao, Jiliang Tang, and Dawei Yin. 2019. Graph neural networks for social recommendation. InProceedings of the Web Conference. ACM, 417–426.

[20]Meherwar Fatima, Maruf Pasha, et al.2017. Survey of machine learning algorithms for disease diagnostic.Journal of Intelligent Learning Systems and Applications9, 01 (2017), 1.

[21]Xinyu Fu, Jiani Zhang, Ziqiao Meng, and Irwin King. 2020. MAGNN: Metapath Aggregated Graph Neural Network for Heterogeneous Graph Embedding. InProceedings of the WWW. ACM, 2331–2341.

[22]Scott Fujimoto, Herke van Hoof, and David Meger. 2018. Addressing Function Approximation Error in Actor-Critic Methods. In Proceedings of the 35th International Conference on Machine Learning (Proceedings of Machine Learning Research, Vol. 80). PMLR, Stockholmsmässan, Stockholm Sweden, 1587–1596.

[23]Yang Gao, Hong Yang, Peng Zhang, Chuan Zhou, and Yue Hu. 2019. Graphnas: Graph neural architecture search with reinforcement learning.arXiv preprint arXiv:1904.09981(2019).

[24]Justin Gilmer, Samuel S Schoenholz, Patrick F Riley, Oriol Vinyals, and George E Dahl. 2017. Neural message passing for quantum chemistry. InProceedings of the ICML. PMLR, 1263–1272.

[25]A. L. Goldberger, L. A. N. Amaral, L. Glass, J. M. Hausdorff, P. Ch. Ivanov, R. G. Mark, J. E. Mietus, G. B. Moody, C. K. Peng, and H. E. Stanley. 2000. PhysioBank, PhysioToolkit, and PhysioNet: components of a new research resource for complex physiologic signals. Circulation101, 23 (2000), E215.

[26]Priya Goyal, Piotr Dollár, Ross Girshick, Pieter Noordhuis, Lukasz Wesolowski, Aapo Kyrola, Andrew Tulloch, Yangqing Jia, and Kaiming He. 2017. Accurate, large minibatch sgd: Training imagenet in 1 hour.arXiv preprint arXiv:1706.02677(2017).

[27]Steve Gregory. 2010. Finding overlapping communities in networks by label propagation.New journal of Physics12, 10 (2010), 103018.

[28]Shengnan Guo, Youfang Lin, Ning Feng, Chao Song, and Huaiyu Wan. 2019. Attention based spatial-temporal graph convolutional networks for traffic flow forecasting. InProceedings of the AAAI, Vol. 33. AAAI Press, 922–929.

[29]Tuomas Haarnoja, Aurick Zhou, Kristian Hartikainen, George Tucker, Sehoon Ha, Jie Tan, Vikash Kumar, Henry Zhu, Abhishek Gupta, Pieter Abbeel, et al. 2018. Soft actor-critic algorithms and applications.arXiv preprint arXiv:1812.05905(2018).

[30]Will Hamilton, Zhitao Ying, and Jure Leskovec. 2017. Inductive representation learning on large graphs. InProceedings of the NIPS. 1024–1034.

[31]Bowen Hao, Jing Zhang, Hongzhi Yin, Cuiping Li, and Hong Chen. 2021. Pre-Training Graph Neural Networks for Cold-Start Users and Items Representation. InProceedings of the WSDM. ACM, 265–273.

[32]Patrick Hart and Alois Knoll. 2020. Graph Neural Networks and Reinforcement Learning for Behavior Generation in Semantic Environments. InIEEE Intelligent Vehicles Symposium (IV). IEEE, 1589–1594.

[33]Hado van Hasselt, Arthur Guez, and David Silver. 2016. Deep reinforcement learning with double Q-Learning. InProceedings of the AAAI. AAAI Press, 2094–2100.

[34]Yu He, Yangqiu Song, Jianxin Li, Cheng Ji, Jian Peng, and Hao Peng. 2019. HeteSpaceyWalk: a heterogeneous spacey random walk for heterogeneous information network embedding. InProceedings of the CIKM. ACM, 639–648.

[35]Huiting Hong, Hantao Guo, Yucheng Lin, Xiaoqing Yang, Zang Li, and Jieping Ye. 2020. An attention-based graph neural network for heterogeneous structural learning. InProceedings of the AAAI. 4132–4139.

[36]Anahita Hosseini, Ting Chen, Wenjun Wu, Yizhou Sun, and Majid Sarrafzadeh. 2018. Heteromed: Heterogeneous information network for medical diagnosis. InProceedings of the CIKM. ACM, 763–772. [37]Junling Hu and Michael P. Wellman. 1998. Multiagent Reinforcement Learning: Theoretical Framework and an Algorithm. InProceedings of the Fifteenth International Conference on Machine Learning (ICML ’98). Morgan Kaufmann Publishers Inc., San Francisco, CA, USA, 242–250.

[38]Ziniu Hu, Yuxiao Dong, Kuansan Wang, and Yizhou Sun. 2020. Heterogeneous graph transformer. InProceedings of the WWW. ACM, 2704–2710.

[39]Jaromír Janisch, Tomáš Pevn`y, and Viliam Lis`y. 2020. Symbolic Relational Deep Reinforcement Learning based on Graph Neural Networks.arXiv preprint arXiv:2009.12462(2020).

[40]Di Jin, Ziyang Liu, Weihao Li, Dongxiao He, and Weixiong Zhang. 2019. Graph convolutional networks meet markov random fields: Semi-supervised community detection in attribute networks. InProceedings of the AAAI. AAAI Press, 152–159.

[41]Alistair EW Johnson, Tom J Pollard, Lu Shen, H Lehman Li-Wei, Mengling Feng, Mohammad Ghassemi, Benjamin Moody, Peter Szolovits, Leo Anthony Celi, and Roger G Mark. 2016. MIMIC-III, a freely accessible critical care database.Scientific data3, 1 (2016), 1–9.

[42]Alistair E. W Johnson, Tom J Pollard, Lu Shen, Li Wei H Lehman, Mengling Feng, Mohammad Ghassemi, Benjamin Moody, Peter Szolovits, Leo Anthony Celi, and Roger G Mark. [n.d.]. MIMIC-III, a freely accessible critical care database.Scientific Data([n. d.]).

[43]Feng Jun, Huang Minlie, Zhao Li, Yang Yang, and Zhu Xiaoyan. 2018. Reinforcement Learning for Relation Classification from Noisy Data. arXiv:1808.08013 [cs.IR]

[44]P. Kaghazgaran, J. Caverlee, and A. Squicciarini. 2018. Combating crowdsourced review manipulators: A neighborhood-based approach. InProceedings of the WSDM. ACM, 306–314.

[45]Anssi Kanervisto, Christian Scheller, and Ville Hautamäki. 2020. Action Space Shaping in Deep Reinforcement Learning. In2020 IEEE Conference on Games (CoG). 479–486.

[46]Seyed Mehran Kazemi and David Poole. 2018. Simple embedding for link prediction in knowledge graphs. InProceedings of the NIPS. 4284–4295.

[47]Thomas N Kipf and Max Welling. 2017. Semi-supervised classification with graph convolutional networks.Proceedings of the ICLR.

[48]Vijay R Konda and John N Tsitsiklis. 2000. Actor-critic algorithms. InProceedings of the NIPS. 1008–1014.

[49]Kwei-Herng Lai, Daochen Zha, Kaixiong Zhou, and Xia Hu. 2020. Policy-GNN: Aggregation Optimization for Graph Neural Networks.

[50]Kai Lei, Meng Qin, Bo Bai, Gong Zhang, and Min Yang. 2019. GCN-GAN: A non-linear temporal link prediction model for weighted dynamic networks. InProceedings of the IEEE INFOCOM. 388–396.

[51]Ao Li, Zhou Qin, Runshi Liu, Yiqun Yang, and Dong Li. 2019. Spam review detection with graph convolutional networks. InProceedings of the 28th ACM International Conference on Information and Knowledge Management. ACM, 2703–2711.

[52]Ruoyu Li and Sheng Wang. 2018. Adaptive Graph Convolutional Neural Networks. InProceedings of the AAAI. AAAI Press, 3546–3553.

[53]Ye Li, Chaofeng Sha, Xin Huang, and Yanchun Zhang. 2018. Community detection in attributed graphs: An embedding approach. In Proceedings of the AAAI. AAAI Press, 338–345.

[54]Timothy P. Lillicrap, Jonathan J. Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuval Tassa, David Silver, and Daan Wierstra. 2019. Continuous control with deep reinforcement learning. arXiv:1509.02971 [cs.LG]

[55]Weiyang Liu, Zhen Liu, James M Rehg, and Le Song. 2019. Neural similarity learning. InProceedings of the NIPS. 5025–5036.

[56]Xin Liu and Tsuyoshi Murata. 2010. Advanced modularity-specialized label propagation algorithm for detecting communities in networks.Physica A: Statistical Mechanics and its Applications389, 7 (2010), 1493–1500.

[57]Ye Liu, Yao Wan, Lifang He, Hao Peng, and Yu Philip S. 2021. KG-BART: Knowledge Graph-Augmented BART for Generative Commonsense Reasoning. InProceedings of the AAAI Conference on Artificial Intelligence, Vol. 35. 6418–6425.

[58]Ziqi Liu, Chaochao Chen, Longfei Li, Jun Zhou, Xiaolong Li, Le Song, and Yuan Qi. 2019. GeniePath: Graph Neural Networks with Adaptive Receptive Paths.Proceedings of the AAAI Conference on Artificial Intelligence33, 01 (Jul. 2019), 4424–4431.

[59]Ziqi Liu, Chaochao Chen, Xinxing Yang, Jun Zhou, Xiaolong Li, and Le Song. 2018. Heterogeneous graph neural networks for malicious account detection. InProceedings of the 27th ACM International Conference on Information and Knowledge Management. 2077–2085.

[60]Zhiwei Liu, Yingtong Dou, Philip S. Yu, Yutong Deng, and Hao Peng. 2020. Alleviating the Inconsistency Problem of Applying Graph Neural Network to Fraud Detection.Proceedings of the SIGIR, 1569–1572.

[61]Zheng Liu, Xiaohan Li, Hao Peng, Lifang He, and Philip S. Yu. 2020. Heterogeneous Similarity Graph Neural Network on Electronic Health Records. InProceedings of the BigData. IEEE.

[62]Chen Lu, Chen Zhi, Tan Bowen, Long Sishan, Gašić Milica, and Yu Kai. 2019. AgentGraph: Toward Universal Dialogue Management With Structured Deep Reinforcement Learning.IEEE/ACM Transactions on Audio, Speech, and Language Processing27, 9 (2019), 1378–1391.

[63]Jake Luo, Christina Eldredge, Chi C Cho, and Ron A Cisler. 2016. Population Analysis of Adverse Events in Different Age Groups Using Big Clinical Trials Data.JMIR Med Inform4, 4 (17 Oct 2016), e30. https://doi.org/10.2196/medinform.6437

[64]Guixiang Ma, Lifang He, Chun-Ta Lu, Weixiang Shao, Philip S. Yu, Alex D Leow, and Ann B Ragin. 2017. Multi-view clustering with graph embedding for connectome analysis. InProceedings of the 2017 ACM on Conference on Information and Knowledge Management. 127–136.

[65]Tengfei Ma, Cao Xiao, Jiayu Zhou, and Fei Wang. 2018. Drug similarity integration through attentive multi-view graph auto-encoders. InProceedings of the 27th International Joint Conference on Artificial Intelligence. 3477–3483.

[66]Julian John McAuley and Jure Leskovec. 2013. From Amateurs to Connoisseurs: Modeling the Evolution of User Expertise through Online Reviews. InProceedings of the 22nd International Conference on World Wide Web(Rio de Janeiro, Brazil)(WWW ’13). Association for Computing Machinery, New York, NY, USA, 897–908.

[67]Changping Meng, Reynold Cheng, Silviu Maniu, Pierre Senellart, and Wangda Zhang. 2015. Discovering meta-paths in large heterogeneous information networks. InProceedings of the WWW. ACM, 754–764.

[68]Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Andrei A Rusu, Joel Veness, Marc G Bellemare, Alex Graves, Martin Riedmiller, Andreas K Fidjeland, Georg Ostrovski, et al.2015. Human-level control through deep reinforcement learning.nature518, 7540 (2015), 529–533.

[69]Arjun Mukherjee, Vivek Venkataraman, Bing Liu, and Natalie Glance. 2013. What Yelp Fake Review Filter Might Be Doing?Proceedings of the International AAAI Conference on Web and Social Media7, 1 (Jun. 2013).

[70]Deepak Nathani, Jatin Chauhan, Charu Sharma, and Manohar Kaul. 2019. Learning Attention-based Embeddings for Relation Prediction in Knowledge Graphs. InProceedings of the ACL. ACL, 4710–4723.

[71]Mark EJ Newman. 2004. Detecting community structure in networks.The European physical journal B38, 2 (2004), 321–330.

[72]Shirui Pan, Ruiqi Hu, Guodong Long, Jing Jiang, Lina Yao, and Chengqi Zhang. 2018. Adversarially regularized graph autoencoder for graph embedding. InProceedings of the IJCAI. AAAI Press, 2609–2615.

[73]Hao Peng, Jianxin Li, Qiran Gong, Yuanxin Ning, Senzhang Wang, and Lifang He. 2020. Motif-Matching Based Subgraph-Level Attentional Convolutional Network for Graph Classification. InProceedings of the AAAI Conference on Artificial Intelligence, Vol. 34. 5387–5394.

[74]Hao Peng, Jianxin Li, Qiran Gong, Yangqiu Song, Yuanxing Ning, Kunfeng Lai, and Philip S. Yu. 2019. Fine-grained event categorization with heterogeneous graph convolutional networks. InProceedings of the IJCAI. AAAI Press, 3238–3245.

[75]Hao Peng, Jianxin Li, Yu He, Yaopeng Liu, Mengjiao Bao, Lihong Wang, Yangqiu Song, and Qiang Yang. 2018. Large-scale hierarchical text classification with recursively regularized deep graph-cnn. InProceedings of the WWW. 1063–1072.

[76]Hao Peng, Jianxin Li, Yangqiu Song, Renyu Yang, Ranjan Rajiv, Philip S. Yu, and He Lifang. 2021. Streaming Social Event Detection and Evolution Discovery in Heterogeneous Information Networks.ACM Transactions on Knowledge Discovery from Data(2021).

[77]Hao Peng, Jianxin Li, Senzhang Wang, Lihong Wang, Qiran Gong, Renyu Yang, Bo Li, Philip S. Yu, and Lifang He. 2019. Hierarchical taxonomy-aware and attentional graph capsule RCNNs for large-scale multi-label text classification.IEEE Transactions on Knowledge and Data Engineering(2019).

[78]Hao Peng, Hongfei Wang, Bowen Du, Md Zakirul Alam Bhuiyan, Hongyuan Ma, Jianwei Liu, Lihong Wang, Zeyu Yang, Linfeng Du, Senzhang Wang, et al.2020. Spatial temporal incidence dynamic graph neural networks for traffic flow forecasting.Information Sciences521 (2020), 277–290.

[79]D. Pozo and J. Contreras. 2011. Finding Multiple Nash Equilibria in Pool-Based Markets: A Stochastic EPEC Approach.IEEE Transactions on Power Systems26, 3 (2011), 1744–1752.

[80]Ruihong Qiu, Zi Huang, Jingjing Li, and Hongzhi Yin. 2020. Exploiting Cross-session Information for Session-based Recommendation with Graph Neural Networks.ACM Transactions on Information Systems (TOIS)38, 3 (2020), 1–23.

[81]Usha Nandini Raghavan, Réka Albert, and Soundar Kumara. 2007. Near linear time algorithm to detect community structures in large-scale networks.Physical review E76, 3 (2007), 036106.

[82]Shebuti Rayana and Leman Akoglu. 2015. Collective opinion spam detection: Bridging review networks and metadata. InProceedings of the SIGKDD. ACM, 985–994.

[83]Michael Schlichtkrull, Thomas N Kipf, Peter Bloem, Rianne Van Den Berg, Ivan Titov, and Max Welling. 2018. Modeling relational data with graph convolutional networks. InProceedings of the ESWC. Springer, 593–607.

[84]John Schulman, Filip Wolski, Prafulla Dhariwal, Alec Radford, and Oleg Klimov. 2017. Proximal policy optimization algorithms.arXiv preprint arXiv:1707.06347(2017).

[85]Chuan Shi, Yitong Li, Jiawei Zhang, Yizhou Sun, and S. Yu Philip. 2016. A survey of heterogeneous information network analysis.IEEE Transactions on Knowledge and Data Engineering29, 1 (2016), 17–37.

[86]Junkai Sun, Junbo Zhang, Qiaofei Li, Xiuwen Yi, Yuxuan Liang, and Yu Zheng. 2020. Predicting citywide crowd flows in irregular regions using multi-view graph convolutional networks.IEEE Transactions on Knowledge and Data Engineering(2020).

[87]Lichao Sun, Yingtong Dou, Carl Yang, Ji Wang, Philip S. Yu, Lifang He, and Bo Li. 2018. Adversarial Attack and Defense on Graph Data: A Survey.arXiv preprint arXiv:1812.10528(2018).

[88]Penghao Sun, Julong Lan, Junfei Li, Zehua Guo, and Yuxiang Hu. 2020. Combining Deep Reinforcement Learning With Graph Neural Networks for Optimal VNF Placement.IEEE Communications Letters(2020).

[89]Qingyun Sun, Hao Peng, Jianxin Li, Senzhang Wang, Xiangyu Dong, Liangxuan Zhao, Philip S. Yu, and Lifang He. 2020. Pairwise Learning for Name Disambiguation in Large-Scale Heterogeneous Academic Networks. (2020), 511–520.

[90]Qingyun Sun, Hao Peng, Jianxin Li, Jia Wu, Yuanxing Ning, Phillip S. Yu, and Lifang He. 2021. SUGAR: Subgraph Neural Network with Reinforcement Pooling and Self-Supervised Mutual Information Mechanism. InProceedings of the Web Conference. 2081–2091.

[91]Yingcheng Sun and Kenneth Loparo. 2019. Opinion spam detection based on heterogeneous information network. InProceedings of the IEEE ICTAI. 1156–1163.

[92]Richard S Sutton and Andrew G Barto. 2018.Reinforcement learning: An introduction. MIT press.

[93]Fawcett Tom. 2006. An introduction to ROC analysis.Pattern Recognition Letters27, 8 (2006), 861–874.

[94]Petar Veličković, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Lio, and Yoshua Bengio. 2018. Graph attention networks. Proceedings of the ICLR.

[95]Vikas Verma, Meng Qu, Alex Lamb, Yoshua Bengio, Juho Kannala, and Jian Tang. 2019. Graphmix: Regularized training of graph neural networks for semi-supervised learning.arXiv preprint arXiv:1909.11715(2019).

[96]Nikil Wale, Ian A Watson, and George Karypis. 2008. Comparison of descriptor spaces for chemical compound retrieval and classification. Knowledge and Information Systems14, 3 (2008), 347–375.

[97]Daixin Wang, Jianbin Lin, Peng Cui, Quanhui Jia, Zhen Wang, Yanming Fang, Quan Yu, Jun Zhou, Shuang Yang, and Yuan Qi. 2019. A Semi-supervised Graph Attentive Network for Financial Fraud Detection. InProceedings of the IEEE ICDM. 598–607.

[98]Jianyu Wang, Rui Wen, Chunming Wu, Yu Huang, and Jian Xion. 2019. Fdgars: Fraudster detection via graph convolutional networks in online app review system. InProceedings of the World Wide Web Conference. 310–316.

[99]Xiao Wang, Deyu Bo, Chuan Shi, Shaohua Fan, Yanfang Ye, and Philip S. Yu. 2020. A Survey on Heterogeneous Graph Embedding: Methods, Techniques, Applications and Sources.arXiv preprint arXiv:2011.14867(2020).

[100]Xiao Wang, Houye Ji, Chuan Shi, et al.2019. Heterogeneous graph attention network. InProceedings of the Web Conference. ACM, 2022–2032.

[101]Yang Wang. 2021. Survey on Deep Multi-Modal Data Analytics: Collaboration, Rivalry, and Fusion.ACM Transactions on Multimedia Computing, Communications, and Applications17, 1s, Article 10 (2021), 25 pages.

[102]Christopher JCH Watkins and Peter Dayan. 1992. Q-learning.Machine learning8, 3-4 (1992), 279–292.

[103]Zonghan Wu, Shirui Pan, Fengwen Chen, Guodong Long, Chengqi Zhang, and S. Yu Philip. 2020. A comprehensive survey on graph neural networks.IEEE Transactions on Neural Networks and Learning Systems(2020).

[104]Yu Xie, Yuanqiao Zhang, Maoguo Gong, Zedong Tang, and Chao Han. 2020. Mgat: Multi-view graph attention networks.Neural Networks132 (2020), 180–189.

[105]Wenhan Xiong, Thien Hoang, and William Yang Wang. 2017. DeepPath: A Reinforcement Learning Method for Knowledge Graph Reasoning. InProceedings of the EMNLP. ACL, 564–573.

[106]Keyulu Xu, Weihua Hu, Jure Leskovec, and Stefanie Jegelka. 2018. How Powerful are Graph Neural Networks?. InProceedings of the ICLR.

[107]Carl Yang, Yichen Feng, Pan Li, Yu Shi, and Jiawei Han. 2018. Meta-graph based hin spectral embedding: Methods, analyses, and insights. InProceedings of the IEEE ICDM. 657–666.

[108]Selim F Yilmaz and Suleyman S Kozat. 2020. Unsupervised Anomaly Detection via Deep Metric Learning with End-to-End Optimization. arXiv preprint arXiv:2005.05865(2020).

[109]Zhitao Ying, Jiaxuan You, Christopher Morris, Xiang Ren, Will Hamilton, and Jure Leskovec. 2018. Hierarchical graph representation learning with differentiable pooling. InProceedings of the NIPS. 4800–4810.

[110]Chen Yu, Wu Lingfei, and J. Zaki Mohammed. 2020. Deep Iterative and Adaptive Learning for Graph Neural Networks.AAAI Workshops (2020).

[111]Baichuan Zhang and Mohammad Al Hasan. 2017. Name disambiguation in anonymized graphs using network embedding. InProceedings of the CIKM. ACM, 1239–1248.

[112]Chuxu Zhang, Dongjin Song, Chao Huang, Ananthram Swami, and Nitesh V Chawla. 2019. Heterogeneous graph neural network. In Proceedings of the SIGKDD. ACM, 793–803.

[113]Muhan Zhang and Yixin Chen. 2018. Link prediction based on graph neural networks. InProceedings of the NIPS. 5165–5175.

[114]Qingheng Zhang, Zequn Sun, Wei Hu, Muhao Chen, Lingbing Guo, and Yuzhong Qu. 2019. Multi-view Knowledge Graph Embedding for Entity Alignment. InProceedings of the IJCAI. 5429–5435.

[115]Shijie Zhang, Hongzhi Yin, Tong Chen, Quoc Viet Nguyen Hung, Zi Huang, and Lizhen Cui. 2020.GCN-Based User Representation Learning for Unifying Robust Recommendation and Fraudster Detection. Association for Computing Machinery, New York, NY, USA, 689–698.

[116]Xi Zhang, Lifang He, Kun Chen, Yuan Luo, Jiayu Zhou, and Fei Wang. 2018. Multi-view graph convolutional network and its applications on neuroimage analysis for parkinson’s disease. InAMIA Annual Symposium Proceedings, Vol. 2018. 1147.

[117]Yiming Zhang, Yujie Fan, Yanfang Ye, Liang Zhao, and Chuan Shi. 2019. Key Player Identification in Underground Forums over Attributed Heterogeneous Information Network Embedding Framework. InProceedings of the CIKM. ACM, 549–558.

[118]Ziwei Zhang, Peng Cui, and Wenwu Zhu. 2020. Deep learning on graphs: A survey.IEEE Transactions on Knowledge and Data Engineering(2020). [119]H. Zheng, M. Xue, H. Lu, S. Hao, H. Zhu, X. Liang, and K. Ross. 2018. Smoke screener or straight shooter: Detecting elite sybil attacks in user-review social networks.Proceedings of the NDSS.

[120]Zhiqiang Zhong, Cheng-Te Li, and Jun Pang. 2020. Reinforcement Learning Enhanced Heterogeneous Graph Neural Network.arXiv preprint arXiv:2010.13735(2020).

[121]Shichao Zhu, Chuan Zhou, Shirui Pan, Xingquan Zhu, and Bin Wang. 2019. Relation structure-aware heterogeneous graph neural network. InProceedings of the IEEE ICDM. 1534–1539.

[122]Xiaojin Zhu and Zoubin Ghahramani. 2002. Learning from labeled and unlabeled data with label propagation. (2002).

[123]Marinka Zitnik and Jure Leskovec. 2017. Predicting multicellular function through multi-layer tissue networks.Bioinformatics33, 14 (2017), i190–i198.
d K. Ross. 2018. Smoke screener or straight shooter: Detecting elite sybil attacks in user-review social networks.Proceedings of the NDSS.

[120]Zhiqiang Zhong, Cheng-Te Li, and Jun Pang. 2020. Reinforcement Learning Enhanced Heterogeneous Graph Neural Network.arXiv preprint arXiv:2010.13735(2020).

[121]Shichao Zhu, Chuan Zhou, Shirui Pan, Xingquan Zhu, and Bin Wang. 2019. Relation structure-aware heterogeneous graph neural network. InProceedings of the IEEE ICDM. 1534–1539.

[122]Xiaojin Zhu and Zoubin Ghahramani. 2002. Learning from labeled and unlabeled data with label propagation. (2002).

[123]Marinka Zitnik and Jure Leskovec. 2017. Predicting multicellular function through multi-layer tissue networks.Bioinformatics33, 14 (2017), i190–i198.