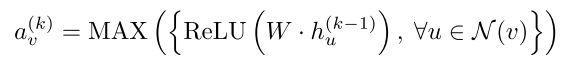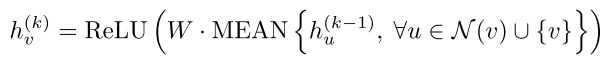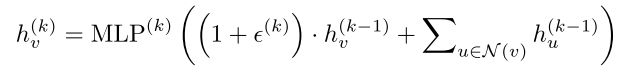- 10月|愿你的青春不负梦想-读书笔记-01
Tracy的小书斋
本书的作者是俞敏洪,大家都很熟悉他了吧。俞敏洪老师是我行业的领头羊吧,也是我事业上的偶像。本日摘录他书中第一章中的金句:『一个人如果什么目标都没有,就会浑浑噩噩,感觉生命中缺少能量。能给我们能量的,是对未来的期待。第一件事,我始终为了进步而努力。与其追寻全世界的骏马,不如种植丰美的草原,到时骏马自然会来。第二件事,我始终有阶段性的目标。什么东西能给我能量?答案是对未来的期待。』读到这里的时候,我便
- 《投行人生》读书笔记
小蘑菇的树洞
《投行人生》----作者詹姆斯-A-朗德摩根斯坦利副主席40年的职业洞见-很短小精悍的篇幅,比较适合初入职场的新人。第一部分成功的职业生涯需要规划1.情商归为适应能力分享与协作同理心适应能力,更多的是自我意识,你有能力识别自己的情并分辨这些情绪如何影响你的思想和行为。2.对于初入职场的人的建议,细节,截止日期和数据很重要截止日期,一种有效的方法是请老板为你所有的任务进行优先级排序。和老板喝咖啡的好
- 【一起学Rust | 设计模式】习惯语法——使用借用类型作为参数、格式化拼接字符串、构造函数
广龙宇
一起学Rust#Rust设计模式rust设计模式开发语言
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档文章目录前言一、使用借用类型作为参数二、格式化拼接字符串三、使用构造函数总结前言Rust不是传统的面向对象编程语言,它的所有特性,使其独一无二。因此,学习特定于Rust的设计模式是必要的。本系列文章为作者学习《Rust设计模式》的学习笔记以及自己的见解。因此,本系列文章的结构也与此书的结构相同(后续可能会调成结构),基本上分为三个部分
- git常用命令笔记
咩酱-小羊
git笔记
###用习惯了idea总是不记得git的一些常见命令,需要用到的时候总是担心旁边站了人~~~记个笔记@_@,告诉自己看笔记不丢人初始化初始化一个新的Git仓库gitinit配置配置用户信息gitconfig--globaluser.name"YourName"gitconfig--globaluser.email"
[email protected]"基本操作克隆远程仓库gitclone查看
- 基于社交网络算法优化的二维最大熵图像分割
智能算法研学社(Jack旭)
智能优化算法应用图像分割算法php开发语言
智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果:5.参考文献:6.Matlab代码摘要:本文介绍基于最大熵的图像分割,并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前,请阅读《图像分割:直方图区域划分及信息统计介绍》htt
- 509. 斐波那契数(每日一题)
lzyprime
lzyprime博客(github)创建时间:2021.01.04qq及邮箱:2383518170leetcode笔记题目描述斐波那契数,通常用F(n)表示,形成的序列称为斐波那契数列。该数列由0和1开始,后面的每一项数字都是前面两项数字的和。也就是:F(0)=0,F(1)=1F(n)=F(n-1)+F(n-2),其中n>1给你n,请计算F(n)。示例1:输入:2输出:1解释:F(2)=F(1)+
- 拥有断舍离的心态,过精简生活--《断舍离》读书笔记
爱吃丸子的小樱桃
不知不觉间房间里的东西越来越多,虽然摆放整齐,但也时常会觉得空间逼仄,令人心生烦闷。抱着断舍离的态度,我开始阅读《断舍离》这本书,希望从书中能找到一些有效的方法,帮助我实现空间、物品上的断舍离。《断舍离》是日本作家山下英子通过自己的经历、思考和实践总结而成的,整体内涵也从刚开始的私人生活哲学的“断舍离”升华成了“人生实践哲学”,接着又成为每个人都能实行的“改变人生的断舍离”,从“哲学”逐渐升华成“
- 四章-32-点要素的聚合
彩云飘过
本文基于腾讯课堂老胡的课《跟我学Openlayers--基础实例详解》做的学习笔记,使用的openlayers5.3.xapi。源码见1032.html,对应的官网示例https://openlayers.org/en/latest/examples/cluster.htmlhttps://openlayers.org/en/latest/examples/earthquake-clusters.
- 高端密码学院笔记285
柚子_b4b4
高端幸福密码学院(高级班)幸福使者:李华第(598)期《幸福》之回归内在深层生命原动力基础篇——揭秘“激励”成长的喜悦心理案例分析主讲:刘莉一,知识扩充:成功=艰苦劳动+正确方法+少说空话。贪图省力的船夫,目标永远下游。智者的梦再美,也不如愚人实干的脚印。幸福早课堂2020.10.16星期五一笔记:1,重视和珍惜的前提是知道它的价值非常重要,当你珍惜了,你就真正定下来,真正的学到身上。2,大家需要
- Day17笔记-高阶函数
~在杰难逃~
Python笔记python开发语言pycharm数据分析
高阶函数【重点掌握】函数的本质:函数是一个变量,函数名是一个变量名,一个函数可以作为另一个函数的参数或返回值使用如果A函数作为B函数的参数,B函数调用完成之后,会得到一个结果,则B函数被称为高阶函数常用的高阶函数:map(),reduce(),filter(),sorted()1.map()map(func,iterable),返回值是一个iterator【容器,迭代器】func:函数iterab
- Day1笔记-Python简介&标识符和关键字&输入输出
~在杰难逃~
Pythonpython开发语言大数据数据分析数据挖掘
大家好,从今天开始呢,杰哥开展一个新的专栏,当然,数据分析部分也会不定时更新的,这个新的专栏主要是讲解一些Python的基础语法和知识,帮助0基础的小伙伴入门和学习Python,感兴趣的小伙伴可以开始认真学习啦!一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码,再通过语言处理程序执行向计算机发送指令,让计算机完成对应的工作,编程
- node.js学习
小猿L
node.jsnode.js学习vim
node.js学习实操及笔记温故node.js,node.js学习实操过程及笔记~node.js学习视频node.js官网node.js中文网实操笔记githubcsdn笔记为什么学node.js可以让别人访问我们编写的网页为后续的框架学习打下基础,三大框架vuereactangular离不开node.jsnode.js是什么官网:node.js是一个开源的、跨平台的运行JavaScript的运行
- 数据仓库——维度表一致性
墨染丶eye
背诵数据仓库
数据仓库基础笔记思维导图已经整理完毕,完整连接为:数据仓库基础知识笔记思维导图维度一致性问题从逻辑层面来看,当一系列星型模型共享一组公共维度时,所涉及的维度称为一致性维度。当维度表存在不一致时,短期的成功难以弥补长期的错误。维度时确保不同过程中信息集成起来实现横向钻取货活动的关键。造成横向钻取失败的原因维度结构的差别,因为维度的差别,分析工作涉及的领域从简单到复杂,但是都是通过复杂的报表来弥补设计
- 【Git】常见命令(仅笔记)
好想有猫猫
GitLinux学习笔记git笔记elasticsearchlinuxc++
文章目录创建/初始化本地仓库添加本地仓库配置项提交文件查看仓库状态回退仓库查看日志分支删除文件暂存工作区代码远程仓库使用`.gitigore`文件让git不追踪一些文件标签创建/初始化本地仓库gitinit添加本地仓库配置项gitconfig-l#以列表形式显示配置项gitconfiguser.name"ljh"#配置user.namegitconfiguser.email"
[email protected]
- 学习“论语”-第59天
春峰轩
12.14子张问政。子曰:“居之无倦,行之以忠。”子张问为政之道。孔子说:“在位尽职不懈怠,执行政令要忠诚。”12.15子曰:“博学于文,约之以礼,亦可以弗畔矣夫!”孔子说:“君子广泛地学习文献,并且用礼节约束自己,也就不会离经叛道了。”12.16子曰:“君子成人之美,不成人之恶。小人反是。”孔子说:“君子成全别人的好事,而不助长别人的坏处。小人则与此相反行事。”知识点:“成人之美,不成人之恶”贯
- 为什么你总是对下属不满意?
ZhaoWu1050
【ZhaoWu的听课笔记】大多数公司,都存在两种问题。我创业四年,更是体会深切。这两种问题就是:老板经常不满意下属的表现;下属总是不知道老板想要什么;虽然这两种问题普遍存在,其实解决方法并不复杂。这节课,我们再聊聊第一个问题:为什么老板经常不满意下属表现?其实,这背后也是一条管理常识。管理学家德鲁克先生早就说过:管理者的任务,不是去改变人。*来自《卓有成效的管理者》只是大多数老板和我一样,都是一边
- 母亲节如何做小红书营销
美橙传媒
小红书的一举一动引起了外界的高度关注。通过爆款笔记和流行话题,我们可以看到“干货”类型的内容在小红书中偏向实用的生活经验共享和生活指南非常受欢迎。根据运营社的分析,这种现象是由小红书用户心智和内容社区背后机制共同决定的。首先,小红书将使用“强搜索”逻辑为用户提供特定的“搜索场景”。在“我必须这样生活”中,大量使用了满足小红书站用户喜好和需求的内容。内容社区自制的高质量内容也吸引了寻找营销新途径的品
- 读书笔记|《遇见孩子,遇见更好的自己》5
抹茶社长
为人父母意味着放弃自己的过去,不要对以往没有实现的心愿耿耿于怀,只有这样,孩子们才能做回自己。985909803.jpg孩子在与父母保持亲密的同时更需要独立,唯有这样,孩子才会成为孩子,父母才会成其为父母。有耐心的人生往往更幸福,给孩子留点余地。认识到养儿育女是对耐心的考验。为失败做好心理准备,教会孩子控制情绪。了解自己的底线,说到底线,有一点很重要,父母之所以发脾气,真正的原因往往在于他们自己,
- 基于Python给出的PDF文档转Markdown文档的方法
程序媛了了
pythonpdf开发语言
注:网上有很多将Markdown文档转为PDF文档的方法,但是却很少有将PDF文档转为Markdown文档的方法。就算有,比如某些网站声称可以将PDF文档转为Markdown文档,尝试过,不太符合自己的要求,而且无法保证文档没有泄露风险。于是本人为了解决这个问题,借助GPT(能使用GPT镜像或者有条件直接使用GPT的,反正能调用GPT接口就行)生成Python代码来完成这个功能。笔记、代码难免存在
- 语文主题教学学习笔记之87
东哥杂谈
“语文主题教学”学习笔记之八十七(0125)今天继续学习小学语文主题教学的实践样态。板块三:教学中体现“书艺”味道。作为四大名著之一的《水浒传》,堪称我国文学宝库之经典。对从《水浒传》中摘选的单元,教师就要了解其原生态,即评书体特点。这也要求教师要了解一些常用的评书行话术语,然后在教学时适时地加入一些,让学生体味其文本中原有的特色。学生也要尽可能地通过朗读的方式,而不单是分析讲解的方式进行学习。细
- Armv8.3 体系结构扩展--原文版
代码改变世界ctw
ARM-TEE-Androidarmv8嵌入式arm架构安全架构芯片TrustzoneSecureboot
快速链接:.ARMv8/ARMv9架构入门到精通-[目录]付费专栏-付费课程【购买须知】:个人博客笔记导读目录(全部)TheArmv8.3architectureextensionTheArmv8.3architectureextensionisanextensiontoArmv8.2.Itaddsmandatoryandoptionalarchitecturalfeatures.Somefeat
- springboot+vue项目实战一-创建SpringBoot简单项目
苹果酱0567
面试题汇总与解析springboot后端java中间件开发语言
这段时间抽空给女朋友搭建一个个人博客,想着记录一下建站的过程,就当做笔记吧。虽然复制zjblog只要一个小时就可以搞定一个网站,或者用cms系统,三四个小时就可以做出一个前后台都有的网站,而且想做成啥样也都行。但是就是要从新做,自己做的意义不一样,更何况,俺就是专门干这个的,嘿嘿嘿要做一个网站,而且从零开始,首先呢就是技术选型了,经过一番思量决定选择-SpringBoot做后端,前端使用Vue做一
- 阅读《认知觉醒》读书笔记
就看看书
本周阅读了周岭的《认知觉醒开启自我改变的原动力》,启发较多,故做读书笔记一则,留待学习。全书共八章,讲述了大脑、潜意识、元认知、专注力、学习力、行动力、情绪力及成本最低的成长之道。具体描述了大脑、焦虑、耐心、模糊、感性、元认知、自控力、专注力、情绪专注、学习专注、匹配、深度、关联、体系、打卡、反馈、休息、清晰、傻瓜、行动、心智宽带、单一视角、游戏心态、早起、冥想、阅读、写作、运动等相关知识点。大脑
- 阅读笔记:阅读方法中的逻辑和转念
施吉涛
聊聊一些阅读的方法论吧,别人家的读书方法刚开始想写,然后就不知道写什么了,因为作者写的非常的“精致”我有一种乡巴佬进城的感觉,看到精美的摆盘,精致的食材不知道该如何下口也就是《阅读的方法》,我们姑且来试一下强劲的大脑篇,第一节:逻辑通俗的来讲,也就是表达的排列和顺序,再进一步就是因果关系和关联实际上书已经看了大概一遍,但直到打算写一下笔记的时候,才发现作者讲的推理更多的是阅读的对象中呈现出的逻辑也
- [Unity]在场景中随机生成不同位置且不重叠的物体
Bartender_Jill
Graphics图形学笔记unity游戏引擎动画
1.前言最近任务需要用到Unity在场景中随机生成物体,且这些物体不能重叠,简单记录一下。参考资料:Howtoensurethatspawnedtargetsdonotoverlap?2.结果与代码结果如下所示:代码如下所示:usingSystem.Collections.Generic;usingUnityEngine;namespaceAssets.Scripts{publicclassNew
- Table列表复现框实现【勾选-搜索-再勾选】
~四时春~
java开发语言elementuivue
Table列表复现框实现【勾选-搜索-再勾选】概要整体架构流程代码实现技术细节注意参考文献概要最近在开发时遇到一个问题,在进行表单渲染时,正常选中没有问题,单如果需要搜索选中时,一个是已选中的不会回填,二是在搜索的结果中进行选中,没有实现,经过排查,查找资料后实现。例如:整体架构流程具体的实现效果如下:代码实现{{scope.row.userName}}已选区{{userItem.userName
- vue+el-table 可输入表格使用上下键进行input框切换
以对_
vue学习记录vue.jsjavascript前端
使用上下键进行完工数量这一列的切换-->//键盘触发事件show(ev,index){letnewIndex;letinputAll=document.querySelectorAll('.table_inputinput');//向上=38if(ev.keyCode==38){if(index==0){//如果是第一行,回到最后一个newIndex=inputAll.length-1}elsei
- 《转介绍方法论》学习笔记
小可乐的妈妈
一、高效转介绍的流程:价值观---执行----方案一)转介绍发生的背景:1、对象:谁向谁转介绍?全员营销,人人参与。①员工的激励政策、客户的转介绍诱因制作客户画像:a信任;支付能力;意愿度;便利度(根据家长具备四个特征的个数分为四类)B性格分类C职业分类D年龄性别②执行:套路,策略,方法,流程2、诱因:为什么要转介绍?认同信任;多方共赢;传递美好;零风险承诺打动人心,超越期待。选择做教育,就是选择
- JAVA学习笔记之23种设计模式学习
victorfreedom
Java技术设计模式androidjava常用设计模式
博主最近买了《设计模式》这本书来学习,无奈这本书是以C++语言为基础进行说明,整个学习流程下来效率不是很高,虽然有的设计模式通俗易懂,但感觉还是没有充分的掌握了所有的设计模式。于是博主百度了一番,发现有大神写过了这方面的问题,于是博主迅速拿来学习。一、设计模式的分类总体来说设计模式分为三大类:创建型模式,共五种:工厂方法模式、抽象工厂模式、单例模式、建造者模式、原型模式。结构型模式,共七种:适配器
- 解决Obsidian写笔记中的<img>标签无法显示图片的问题
全能全知者
笔记
Obsidian中写md笔记如果使用标签会显示不出图案,后来才知道因为Obsidian的问题导致只能用绝对路径定位。所以我本人写了一个py插件,将md笔记里的img标签批量替换成Obsidian能够读取的形式。安装FixObsImgDpy:pipinstallFixObsImgDpy安装完成后在需要修复的md文件的父目录下运行命令:FixObsImgDpy就会自动修复父目录以下的全部md文件 仓库
- ASM系列六 利用TreeApi 添加和移除类成员
lijingyao8206
jvm动态代理ASM字节码技术TreeAPI
同生成的做法一样,添加和移除类成员只要去修改fields和methods中的元素即可。这里我们拿一个简单的类做例子,下面这个Task类,我们来移除isNeedRemove方法,并且添加一个int 类型的addedField属性。
package asm.core;
/**
* Created by yunshen.ljy on 2015/6/
- Springmvc-权限设计
bee1314
springWebjsp
万丈高楼平地起。
权限管理对于管理系统而言已经是标配中的标配了吧,对于我等俗人更是不能免俗。同时就目前的项目状况而言,我们还不需要那么高大上的开源的解决方案,如Spring Security,Shiro。小伙伴一致决定我们还是从基本的功能迭代起来吧。
目标:
1.实现权限的管理(CRUD)
2.实现部门管理 (CRUD)
3.实现人员的管理 (CRUD)
4.实现部门和权限
- 算法竞赛入门经典(第二版)第2章习题
CrazyMizzz
c算法
2.4.1 输出技巧
#include <stdio.h>
int
main()
{
int i, n;
scanf("%d", &n);
for (i = 1; i <= n; i++)
printf("%d\n", i);
return 0;
}
习题2-2 水仙花数(daffodil
- struts2中jsp自动跳转到Action
麦田的设计者
jspwebxmlstruts2自动跳转
1、在struts2的开发中,经常需要用户点击网页后就直接跳转到一个Action,执行Action里面的方法,利用mvc分层思想执行相应操作在界面上得到动态数据。毕竟用户不可能在地址栏里输入一个Action(不是专业人士)
2、<jsp:forward page="xxx.action" /> ,这个标签可以实现跳转,page的路径是相对地址,不同与jsp和j
- php 操作webservice实例
IT独行者
PHPwebservice
首先大家要简单了解了何谓webservice,接下来就做两个非常简单的例子,webservice还是逃不开server端与client端。我测试的环境为:apache2.2.11 php5.2.10做这个测试之前,要确认你的php配置文件中已经将soap扩展打开,即extension=php_soap.dll;
OK 现在我们来体验webservice
//server端 serve
- Windows下使用Vagrant安装linux系统
_wy_
windowsvagrant
准备工作:
下载安装 VirtualBox :https://www.virtualbox.org/
下载安装 Vagrant :http://www.vagrantup.com/
下载需要使用的 box :
官方提供的范例:http://files.vagrantup.com/precise32.box
还可以在 http://www.vagrantbox.es/
- 更改linux的文件拥有者及用户组(chown和chgrp)
无量
clinuxchgrpchown
本文(转)
http://blog.163.com/yanenshun@126/blog/static/128388169201203011157308/
http://ydlmlh.iteye.com/blog/1435157
一、基本使用:
使用chown命令可以修改文件或目录所属的用户:
命令
- linux下抓包工具
矮蛋蛋
linux
原文地址:
http://blog.chinaunix.net/uid-23670869-id-2610683.html
tcpdump -nn -vv -X udp port 8888
上面命令是抓取udp包、端口为8888
netstat -tln 命令是用来查看linux的端口使用情况
13 . 列出所有的网络连接
lsof -i
14. 列出所有tcp 网络连接信息
l
- 我觉得mybatis是垃圾!:“每一个用mybatis的男纸,你伤不起”
alafqq
mybatis
最近看了
每一个用mybatis的男纸,你伤不起
原文地址 :http://www.iteye.com/topic/1073938
发表一下个人看法。欢迎大神拍砖;
个人一直使用的是Ibatis框架,公司对其进行过小小的改良;
最近换了公司,要使用新的框架。听说mybatis不错;就对其进行了部分的研究;
发现多了一个mapper层;个人感觉就是个dao;
- 解决java数据交换之谜
百合不是茶
数据交换
交换两个数字的方法有以下三种 ,其中第一种最常用
/*
输出最小的一个数
*/
public class jiaohuan1 {
public static void main(String[] args) {
int a =4;
int b = 3;
if(a<b){
// 第一种交换方式
int tmep =
- 渐变显示
bijian1013
JavaScript
<style type="text/css">
#wxf {
FILTER: progid:DXImageTransform.Microsoft.Gradient(GradientType=0, StartColorStr=#ffffff, EndColorStr=#97FF98);
height: 25px;
}
</style>
- 探索JUnit4扩展:断言语法assertThat
bijian1013
java单元测试assertThat
一.概述
JUnit 设计的目的就是有效地抓住编程人员写代码的意图,然后快速检查他们的代码是否与他们的意图相匹配。 JUnit 发展至今,版本不停的翻新,但是所有版本都一致致力于解决一个问题,那就是如何发现编程人员的代码意图,并且如何使得编程人员更加容易地表达他们的代码意图。JUnit 4.4 也是为了如何能够
- 【Gson三】Gson解析{"data":{"IM":["MSN","QQ","Gtalk"]}}
bit1129
gson
如何把如下简单的JSON字符串反序列化为Java的POJO对象?
{"data":{"IM":["MSN","QQ","Gtalk"]}}
下面的POJO类Model无法完成正确的解析:
import com.google.gson.Gson;
- 【Kafka九】Kafka High Level API vs. Low Level API
bit1129
kafka
1. Kafka提供了两种Consumer API
High Level Consumer API
Low Level Consumer API(Kafka诡异的称之为Simple Consumer API,实际上非常复杂)
在选用哪种Consumer API时,首先要弄清楚这两种API的工作原理,能做什么不能做什么,能做的话怎么做的以及用的时候,有哪些可能的问题
- 在nginx中集成lua脚本:添加自定义Http头,封IP等
ronin47
nginx lua
Lua是一个可以嵌入到Nginx配置文件中的动态脚本语言,从而可以在Nginx请求处理的任何阶段执行各种Lua代码。刚开始我们只是用Lua 把请求路由到后端服务器,但是它对我们架构的作用超出了我们的预期。下面就讲讲我们所做的工作。 强制搜索引擎只索引mixlr.com
Google把子域名当作完全独立的网站,我们不希望爬虫抓取子域名的页面,降低我们的Page rank。
location /{
- java-归并排序
bylijinnan
java
import java.util.Arrays;
public class MergeSort {
public static void main(String[] args) {
int[] a={20,1,3,8,5,9,4,25};
mergeSort(a,0,a.length-1);
System.out.println(Arrays.to
- Netty源码学习-CompositeChannelBuffer
bylijinnan
javanetty
CompositeChannelBuffer体现了Netty的“Transparent Zero Copy”
查看API(
http://docs.jboss.org/netty/3.2/api/org/jboss/netty/buffer/package-summary.html#package_description)
可以看到,所谓“Transparent Zero Copy”是通
- Android中给Activity添加返回键
hotsunshine
Activity
// this need android:minSdkVersion="11"
getActionBar().setDisplayHomeAsUpEnabled(true);
@Override
public boolean onOptionsItemSelected(MenuItem item) {
- 静态页面传参
ctrain
静态
$(document).ready(function () {
var request = {
QueryString :
function (val) {
var uri = window.location.search;
var re = new RegExp("" + val + "=([^&?]*)", &
- Windows中查找某个目录下的所有文件中包含某个字符串的命令
daizj
windows查找某个目录下的所有文件包含某个字符串
findstr可以完成这个工作。
[html]
view plain
copy
>findstr /s /i "string" *.*
上面的命令表示,当前目录以及当前目录的所有子目录下的所有文件中查找"string&qu
- 改善程序代码质量的一些技巧
dcj3sjt126com
编程PHP重构
有很多理由都能说明为什么我们应该写出清晰、可读性好的程序。最重要的一点,程序你只写一次,但以后会无数次的阅读。当你第二天回头来看你的代码 时,你就要开始阅读它了。当你把代码拿给其他人看时,他必须阅读你的代码。因此,在编写时多花一点时间,你会在阅读它时节省大量的时间。让我们看一些基本的编程技巧: 尽量保持方法简短 尽管很多人都遵
- SharedPreferences对数据的存储
dcj3sjt126com
SharedPreferences简介: &nbs
- linux复习笔记之bash shell (2) bash基础
eksliang
bashbash shell
转载请出自出处:
http://eksliang.iteye.com/blog/2104329
1.影响显示结果的语系变量(locale)
1.1locale这个命令就是查看当前系统支持多少种语系,命令使用如下:
[root@localhost shell]# locale
LANG=en_US.UTF-8
LC_CTYPE="en_US.UTF-8"
- Android零碎知识总结
gqdy365
android
1、CopyOnWriteArrayList add(E) 和remove(int index)都是对新的数组进行修改和新增。所以在多线程操作时不会出现java.util.ConcurrentModificationException错误。
所以最后得出结论:CopyOnWriteArrayList适合使用在读操作远远大于写操作的场景里,比如缓存。发生修改时候做copy,新老版本分离,保证读的高
- HoverTree.Model.ArticleSelect类的作用
hvt
Web.netC#hovertreeasp.net
ArticleSelect类在命名空间HoverTree.Model中可以认为是文章查询条件类,用于存放查询文章时的条件,例如HvtId就是文章的id。HvtIsShow就是文章的显示属性,当为-1是,该条件不产生作用,当为0时,查询不公开显示的文章,当为1时查询公开显示的文章。HvtIsHome则为是否在首页显示。HoverTree系统源码完全开放,开发环境为Visual Studio 2013
- PHP 判断是否使用代理 PHP Proxy Detector
天梯梦
proxy
1. php 类
I found this class looking for something else actually but I remembered I needed some while ago something similar and I never found one. I'm sure it will help a lot of developers who try to
- apache的math库中的回归——regression(翻译)
lvdccyb
Mathapache
这个Math库,虽然不向weka那样专业的ML库,但是用户友好,易用。
多元线性回归,协方差和相关性(皮尔逊和斯皮尔曼),分布测试(假设检验,t,卡方,G),统计。
数学库中还包含,Cholesky,LU,SVD,QR,特征根分解,真不错。
基本覆盖了:线代,统计,矩阵,
最优化理论
曲线拟合
常微分方程
遗传算法(GA),
还有3维的运算。。。
- 基础数据结构和算法十三:Undirected Graphs (2)
sunwinner
Algorithm
Design pattern for graph processing.
Since we consider a large number of graph-processing algorithms, our initial design goal is to decouple our implementations from the graph representation
- 云计算平台最重要的五项技术
sumapp
云计算云平台智城云
云计算平台最重要的五项技术
1、云服务器
云服务器提供简单高效,处理能力可弹性伸缩的计算服务,支持国内领先的云计算技术和大规模分布存储技术,使您的系统更稳定、数据更安全、传输更快速、部署更灵活。
特性
机型丰富
通过高性能服务器虚拟化为云服务器,提供丰富配置类型虚拟机,极大简化数据存储、数据库搭建、web服务器搭建等工作;
仅需要几分钟,根据CP
- 《京东技术解密》有奖试读获奖名单公布
ITeye管理员
活动
ITeye携手博文视点举办的12月技术图书有奖试读活动已圆满结束,非常感谢广大用户对本次活动的关注与参与。
12月试读活动回顾:
http://webmaster.iteye.com/blog/2164754
本次技术图书试读活动获奖名单及相应作品如下:
一等奖(两名)
Microhardest:http://microhardest.ite