【回归预测-BP预测】基于思维进化算法优化BP神经网络在非线性函数拟合中的应用（Matlab代码实现）

目录

1 概述

2 BP神经网络 

3 思维进化算法

4 思维进化算法优化BP神经网络的步骤​​​​​​​

5 运行结果

6 参考文献

7 Matlab代码实现

---

1 概述

随着项目的日益繁杂多元,在部分项目实施过程中,可能存在着要对大批采集到的数据做函数拟合的需求。然而,这些数据是非线性的,根据目前的传统拟合方法,很难达到项目所要求的拟合精度。
据调查分析,对于非线性函数的并行化处理,即同时执行两个或多个处理的一种计算方法,人工神经网络更具有针对性,同时依靠它自身极强的自我学习能力和学习算法时对新数据的适应能力,为非线性函数拟合问题提供了一种较为高效的解决方案。张宝堃等人1使用BP神经网络来对一组单输入单输出这样的单变量非线性函数进行拟合,尽管BP神经网络对于非线性函数有很强的射影能力,但是这种方法仍然存在着只在一定范围区域内最优的问题。徐富强等人[2则首先通过遗传算法对BP神经网络的初始权重和临界值(也叫临界值)进行改良筛选,然后选择了优化后的BP神经网络来拟合非线性函数,尽管这种方法具有很强的全局搜索能力,但是误差仍然比较大。沈学利等人[3使用粒子群优化的方法训练BP神经网络参数来处理非线性函数拟合的问题,这种方法对非线性函数的拟合起到了一定的作用,但是结果仍然存在着预测精度较低的缺点,并且极易造成局部最优的后果。基于以上算法存在的不足,在论文中对思维进化算法作了深入的研究,通过调整筛选BP神经网络初始权重和临界值,在处理非线性函数拟合上取得了新成果，同时也证明了思维进化算法的强拟合性。

使用传统的BP神经网络直接对非线性函数的变化进行预测和拟合,存在着函收敛序列向其极限逼近的速度慢,预测拟合精度低等不足。针对BP神经网络的优点和不足，论文通过描述对一种理论上优势极强的非线性思维方式和进化过程的算法,适当的调整其初始权重和临界值,使其自身更加容易得到一定的优化。通过它的拓扑结构构造出思维进化算法和模型,值用思维进化算法中的最优解替代它的初始权重和临界,选取多个非线性函数,用MATLAB做拟合仿真实验,对比优化前后测得值与真实值之差,经过对实验结果的不断分析总结，能够得出优化后的B神经网络速度收敛更快的结果。

2 BP神经网络 

BP算法的执行顺序可以总结为以下几点
(1)给网络权重置初值,即将非零随机数置于每一层的权重上。
(2)输入一个数据样本和其相应的目标输出。
(3)根据权重,计算出各个层的实际输出。
(4)由各层的实际输出值和目标输出值计算出它们的预测误差。
(5)多次改变网络的权重和临界值,使其预测误差逐渐向最小值逼近。
(6)求出所有层的权重之后,可以根据所给结束条件确定是否继续调整权重。若符合条件,则停止算法;反之,若不符合条件,则返回执行(3)—(6)步。

3 思维进化算法

思维进化算法的基本思路是
(1)通过随机函数来获得所需数量的个体,以使它们散落分布在整个解空间中。
(2)根据得分函数,计算出所有个体各自的得分,然后从中选取部分得分最高的个体,将选中个体以自身为核心,并围绕它们产生一定数量的新个体，形成一个个子种群,并分裂为优胜子种群和临时子群。
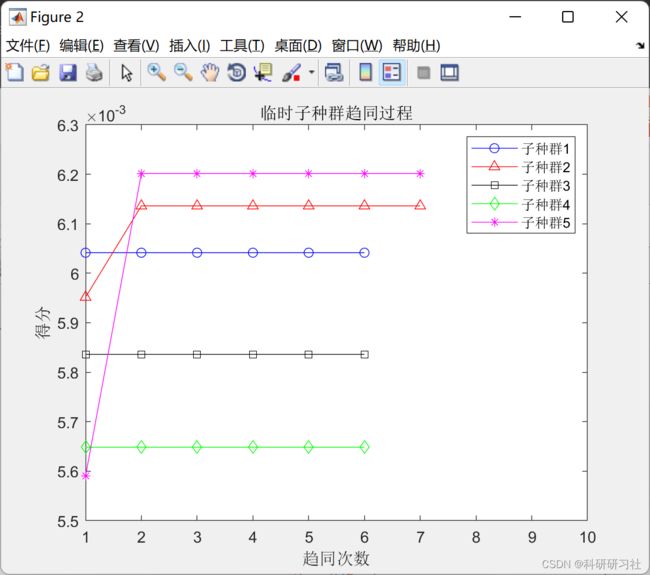
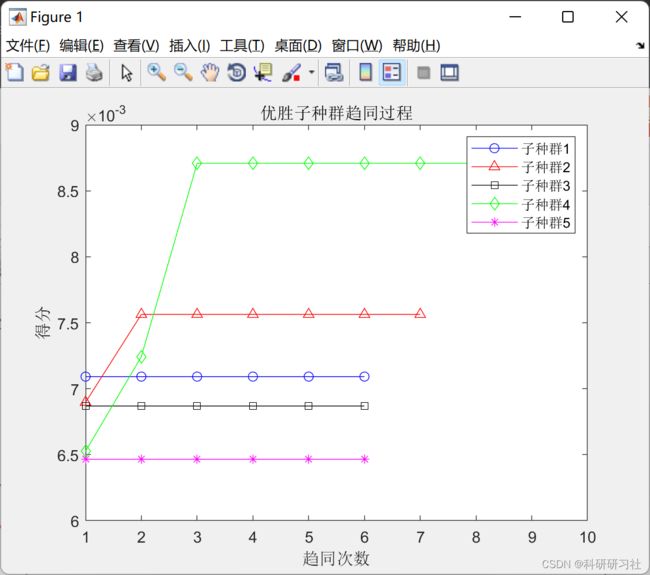
( 3)分别在各个子种群内分别进行趋同操作,使它们互相竞争,最终寻找出获胜个体,并记录其得分,当作最终得分。
(4)异化操作在整个解空间内部实行,假如存在某成熟临时优胜子种群的得分比另一优胜子种群的低,则其被这个优胜子种群代替;假如某成熟临时子种群的得分比任何优胜子种群的得分都低,则将其弃用。被取代或弃用的子群体中所有个体将再次散落在解空间中,组成一个新的临时子种群。

4 思维进化算法优化BP神经网络的步骤

部分代码： 

function initpop = initpop_generate(popsize,S1,S2,S3,S4,P,T,Pt,Tt)
% 编码长度（权值/阈值总个数）
S = S1*S2 + S2*S3 + S3*S4+S2 + S3+S4;

% 预分配初始种群数组
initpop = zeros(popsize,S+1);

for i = 1:popsize
    % 随机产生一个个体[-1,1]
    x = rand(1,S)*2 - 1;
    
    % 前S1*S2个编码为W1（输入层与第一个隐含层间权值）
    temp = x(1:S1*S2);
    W1 = reshape(temp,S2,S1);
    
    % 接着的S2*S3个编码为W2（隐含层与第二隐含层间权值）
    temp = x(S1*S2+1:S1*S2+S2*S3);
    W2 = reshape(temp,S3,S2);
    
    % 接着的S3*S4个编码为W3（隐含层与第二隐含层间权值）
    temp = x(S1*S2+S2*S3+1:S1*S2+S2*S3+S3*S4);
    W3 = reshape(temp,S4,S3);
    
    % 接着的S2个编码为B1（第一隐含层神经元阈值）
    temp = x(S1*S2+S2*S3+S3*S4+1:S1*S2+S2*S3+S3*S4+S2);
    B1 = reshape(temp,S2,1);
    % 接着的S3个编码为B2（第2隐含层神经元阈值）
    temp = x(S1*S2+S2*S3+S3*S4+S2+1:S1*S2+S2*S3+S3*S4+S2+S3);
    B2 = reshape(temp,S3,1);
    %接着的S4个编码B3（输出层神经元阈值）
    temp = x(S1*S2+S2*S3+S3*S4+S2+S3+1:end);
    B3 = reshape(temp,S4,1);
  
net=newff(P,T,[S2 S3]);
net.trainParam.showWindow=0;
net.trainParam.epochs=20;
net.trainParam.lr=0.1;
net.trainParam.goal=0.00001;
net.trainParam.show=1;
% 将寻优的值赋给双隐层BP网络
net.iw{1,1}=W1;
net.lw{2,1}=W2;
net.lw{3,2}=W3;
net.b{1}=B1;
net.b{2}=B2;
net.b{3}=B3;
%网络训练
net=train(net,P,T);
an=sim(net,Pt);
error=mse(an-Tt);
    % 思维进化算法的得分
    val = error;
    % 个体与得分合并
    initpop(i,:) = [x val];
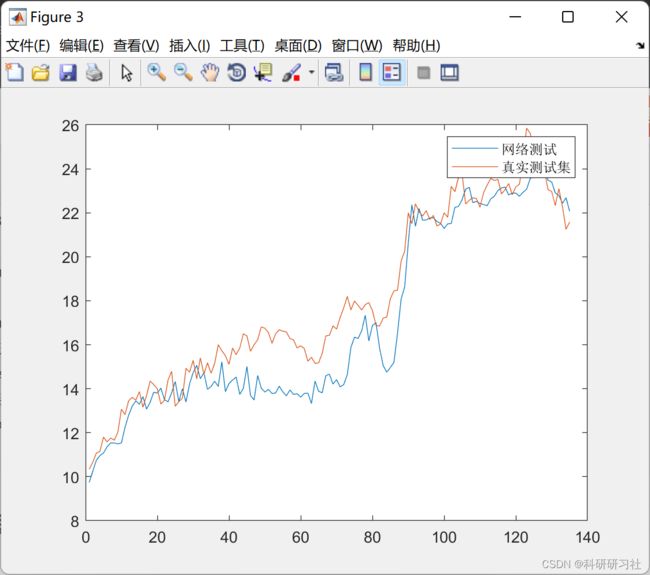
end

5 运行结果

 

 

6 参考文献

部分理论引用网络文献，如有侵权请联系删除。

[1]王永亮.思维进化算法优化BP神经网络在非线性函数拟合中的应用[J].忻州师范学院学报,2021,37(05):35-41.

7 Matlab代码实现