C++卷积神经网络实例：tiny_cnn代码详解（7）——fully_connected_layer层结构类分析

　　之前的博文中已经将卷积层、下采样层进行了分析，在这篇博文中我们对最后一个顶层层结构fully_connected_layer类（全连接层）进行分析：

　　一、卷积神经网路中的全连接层

　　在卷积神经网络中全连接层位于网络模型的最后部分，负责对网络最终输出的特征进行分类预测，得出分类结果：

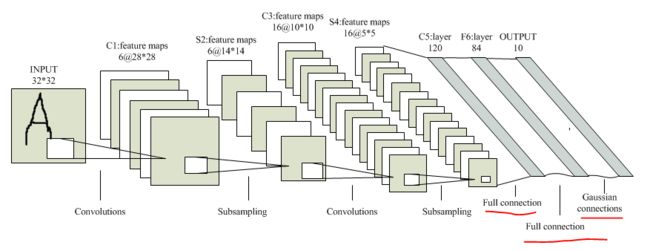
　　LeNet-5模型中的全连接层分为全连接和高斯连接，该层的最终输出结果即为预测标签，例如这里我们需要对MNIST数据库中的数据进行分类预测，其中的数据一共有10类（数字0~9），因此全全连接层的最终输出就是一个10维的预测结果向量，哪一维的值为非零，则预测结果对应的就是几。

　　二、fully_connected_layer类结构

　　与之前卷积层和下采样层不同的是，这里的全连接层fully_connected_layer类继承自基类layer，其中类成员一共可分为四大部分：成员变量、构造函数、前向传播函数、反向传播函数。

　　2.1 成员变量

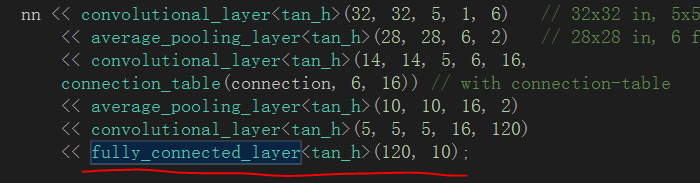
　　fully_connected_layer类的成员变量只有一个，就是一个Filter类型的变量：

　　而这里的Filter是通过类模板参数传入的一个缺省filter_none类型，具体如下：

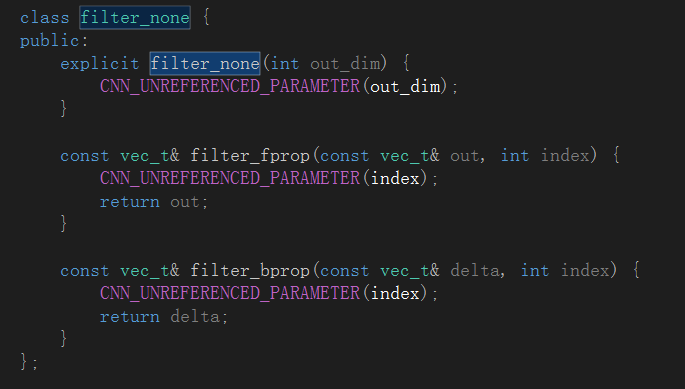
　　至于filter_none类型，从名称判断应该是一个和滤波器核相关的类封装，具体定义在dropout.h文件中：

　　有关dropout.h文件中封装的相关类的详细信息我会在之后的博文中进行详细的介绍，这里先留一个坑，不过事先透漏一点，卷积神经网络中的dropout本质上是为了改善网络过拟合性能而设计的。

　　2.2 构造函数

　　构造函数极其简单，单纯的调用了基类layer的构造函数：

　　至于基类layer，里面封装了大量的虚函数以及纯虚函数，并给出了网络层基本的框架设定，对layer_base类进行了一部分实例化，这几点我们以后会详细说的。

　　2.3 前向传播函数

　　众所周知，卷积神经网络在训练时和BP神经网络的训练极其相似，包括一个样本预测的前向传播过程和误差的反向传播过程。首先前向传播函数的代码如下：

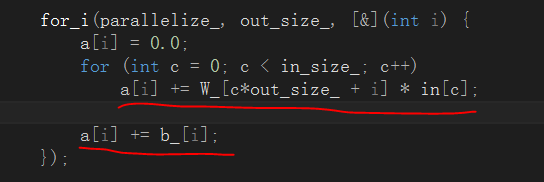
        const vec_t& forward_propagation(const vec_t& in, size_t index) {
            vec_t &a = a_[index];
            vec_t &out = output_[index];

            for_i(parallelize_, out_size_, [&](int i) {
                a[i] = 0.0;
                for (int c = 0; c < in_size_; c++)
                    a[i] += W_[c*out_size_ + i] * in[c];

                a[i] += b_[i];
            });

            for_i(parallelize_, out_size_, [&](int i) {
                out[i] = h_.f(a, i);
            });

            auto& this_out = filter_.filter_fprop(out, index);

            return next_ ? next_->forward_propagation(this_out, index) : this_out;
        }

　　从代码中可以看出这个前向传播函数本质上属于一个递归函数，用递归的方式实现层层传播的功能：

　　在前向传播的过程中，主要有两个阶段，一是通过当前层的卷积核和偏置完成对输入数据的映射：

　　从代码中可见，卷积层的映射过程本质上就是一个卷积操作，然后在对卷积结果累加偏置。第二个阶段就是将卷积层的映射结果送入激活函数中进行处理：

　　激活函数的主要作用是对卷积层的映射输出进行规范化，调整期数据分布。经典的激活函数是Sigmoid函数，主要对输出特征进行平滑。在之后学者又提出Relu类型的激活函数，主要是对输出特征进行稀疏化规范，使其更接近于人脑的视觉映射机理。在tiny_cnn中作者封装了sigmoid、relu、leaky_relu、softmax、tan_h、tan_hp1m2等激活函数，这些类都定义在activation命名空间中，具体在activation_function.h文件中，在后续的篇幅中我会专门拿出一篇博文的篇幅对tiny_cnn的激活函数做集中的分析。

　　2.4 反向传播函数

　　反向传播算法是BP类型神经网络的经典特征，大部分都采用随机梯度下降法对误差进行求导和传播。由于反向传播算法涉及到误差的求偏导、灵敏度传递等概念，导致其在原理上相对于前向传播过程显得更为复杂，代码实现也较为繁琐，我们这里只是先给出反向传播的代码，在后续的博文中在针对这个传播过程进行更文详细的分析，OK，又是一个坑：

    const vec_t& back_propagation(const vec_t& current_delta, size_t index) {
            const vec_t& curr_delta = filter_.filter_bprop(current_delta, index);
            const vec_t& prev_out = prev_->output(index);
            const activation::function& prev_h = prev_->activation_function();
            vec_t& prev_delta = prev_delta_[index];
            vec_t& dW = dW_[index];
            vec_t& db = db_[index];

            for (int c = 0; c < this->in_size_; c++) {
                // propagate delta to previous layer
                // prev_delta[c] += current_delta[r] * W_[c * out_size_ + r]
                prev_delta[c] = vectorize::dot(&curr_delta[0], &W_[c*out_size_], out_size_);
                prev_delta[c] *= prev_h.df(prev_out[c]);
            }

            for_(parallelize_, 0, out_size_, [&](const blocked_range& r) {
                // accumulate weight-step using delta
                // dW[c * out_size + i] += current_delta[i] * prev_out[c]
                for (int c = 0; c < in_size_; c++)
                    vectorize::muladd(&curr_delta[0], prev_out[c], r.end() - r.begin(), &dW[c*out_size_ + r.begin()]);

                for (int i = r.begin(); i < r.end(); i++) 
                    db[i] += curr_delta[i];
            });

            return prev_->back_propagation(prev_delta_[index], index);
        }

　　四、注意事项

　　1、卷积层和下采样层的前向/反向传播函数

　　在fully_connected_layer类中我们发现其内部封装了前向/反向传播函数，但在之前介绍的卷积层和均值下采样层中我们并没有发现前向/反向传播函数的影子，但前向/反向传播函数确实是一个全局的过程，不可能出现断层，因此仔细研究就会发现原来作者是将convolutional_layer类和average_pooling_layer对应的前向/反向传播函数封装在了它们共同的基类：partial_connected_layer中了。

　　2、前向传播函数和反向传播函数

　　在这篇博文中我为后续的博文中挖下了很多大坑，尤其像前向/反向传播函数这种卷积神经网络训练的精华部分，是最能体现作者编程功力和框架设计功力的地方，一两篇博文都不一定能讲的清楚，所以请大家不要着急，我会尽快把其中的玄机弄明白，然后用通俗的语言进行解释的，所以说，坑一定会都一一填上的。

如果觉得这篇文章对您有所启发，欢迎关注我的公众号，我会尽可能积极和大家交流，谢谢。