deep learning知识以及面试题

优化算法

优化器包含一阶、二阶方法

** 一阶方法： ** 随机梯度下降(SGD)、动量(Momentum)、牛顿动量法(Nesterov)、自适应梯度AdaGrad()、均方差传播(RMSProp)、Adam、Nadam等

** 二阶方法： **牛顿法、拟牛顿法、共轭梯度法(CG)、BFGS、L-BFGS。

自适应优化算法有哪些？

• AdaGrad : 累积梯度平方
• RMSProp: 累积梯度平方的滑动平均
• Adam : 带Momentum的RMSProp，即同时使用梯度的一、二阶矩

** 梯度下降陷入局部最优有什么解决办法？ **
可以用BGD、SGD、MBGD、momentum，RMSprop，Adam等方法来避免陷入局部最优

1. 梯度下降法原理

梯度下降法，是求解无约束最优化问题的一种最常用的方法，在对损失函数最小化时经常使用。
梯度下降法是一种迭代算法。选取适当的初值x(0)，不断迭代，更新x的值，进行目标函数的极小化，直到收敛。
$$J(\theta )=\frac{1}{2m}\sum _{j=1}^m[h_{\theta }(x^i)-y^i{]}^2$$
其中，J(θ)是损失函数，m代表每次取多少样本进行训练，如果采用SGD进行训练，那每次随机取一组样本，m=1；如果是批处理，则m等于每次抽取作为训练样本的数量。θ是参数，对应（1式）的θ1和θ2。求出了θ1和θ2，h(x)的表达式就出来了:
$$h(\theta )=\sum {\theta }_j{x}_j={\theta }_1{x}_1+{\theta }_2{x}_2$$
我们的目标是让损失函数J(θ)的值最小，根据梯度下降法，首先要用J(θ)对θ求偏导
由于是要最小化损失函数，所以参数θ按其负梯度方向来更新：
$${\theta }^{\prime }={\theta }_j-\frac{\sigma J(\theta )}{\sigma {\theta }_j}={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m(y^i-h_{\theta }(x^i))x_j^i$$

批量梯度下降（BGD）

批量梯度下降法是梯度下降法最常用的形式，具体做法也就是在更新参数时使用所有的样本来进行。
$${\theta }_j:={\theta }_j+\alpha \sum _{i=1}^m(y_i-{\theta }_i^T{x}^i)x_j$$
coding:

for i in range(nb_epochs):
    params_grad = evaluate_gradient(loss_function, data, params)
    params = params - learning_rate * params_grad

**pros: **

• a. 一次迭代是对所有样本进行计算，此时利用矩阵进行操作，实现了并行
• b. 由全数据集确定的方向能够更好地代表样本总体，从而更准确地朝向极值所在的方向，当目标函数是凸函数时BGD一定能找到全局最优解。
  **cons: **
• a. 当样本数目 m 很大时，每迭代一步都需要对所有样本计算，训练过程会很慢。
• b. 不能投入新数据实时更新模型。

随机梯度下降（SGD）

随机梯度下降法求梯度时选取一个样本j来求梯度。
$${\theta }_j:={\theta }_j+\alpha (y_i-{\theta }_i^T{x}^i)x_j$$

for i in range(epochs): 
	np.random.shuffle(data)
	for example in data:
		params_grad = evaluate_gradient(loss_function , example ,params)
        params = params - learning_rate * params_grad

**pros: **

• a. 更新速度大大加快。
  **cons: **
• a. 准确度下降。由于即使在目标函数为强凸函数的情况下，SGD仍旧无法做到线性收敛。
• b. 可能会收敛到局部最优，由于单个样本并不能代表全体样本的趋势。
• c. 不易于并行实现。SGD 因为更新比较频繁，会造成 cost function 有严重的震荡

小批量梯度下降（Mini batch GD）

小批量梯度下降法是是对于m个样本，我们采用x个样本来迭代，1 $${\theta }_j:=\theta -\eta \cdot {\nabla }_{\theta }J(\theta ;x^{i:i+n};y^{i:i+n})$$

for i in range(epochs): 
	np.random.shuffle(data)
	for batch in get_batches(data, batch_size=50):
		params_grad = evaluate_gradient(loss_function, batch, params)
        params = params - learning_rate * params_grad

**pros: **

• a. 通过矩阵运算，每次在一个batch上优化神经网络参数并不会比单个数据慢太多
• b. 可实现并行化。
  **cons: **
• a. 不能保证很好的收敛性。

2. 梯度下降算法改进

动量梯度下降法（Momentum）

Momentum 通过加入 $ \gamma* v{t-1} $ ,可以加速SGD，并且抑制震荡。
momentum即动量，它模拟的是物体运动时的惯性，即更新的时候在一定程度上保留之前更新的方向，同时利用当前batch的梯度微调最终的更新方向，$ \gamma $一般为0.9。
$$\begin{gathered} V_t=\gamma v_{t-1}+\eta {\nabla }_{\theta }J(\theta ) \\ \theta =\theta -v_t \end{gathered}$$
**cons: ** 虽然会加速收敛速度，但是由于惯性原因需要慢慢适应反向梯度情况。

Nesterov accelerated 下降法（NAG）

用$\theta -\gamma v_{t-1}$来近似当做参数下一步会变成的值，则在计算梯度时，不是在当前位置，而是未来的位置上。仍然是动量法，只是它要求这个下降更加智能。这个算法就可以对低频的参数做较大的更新，对高频的做较小的更新，也因此，对于稀疏的数据它的表现很好，很好地提高了 SGD 的鲁棒性。
$$\begin{gathered} V_t=\gamma v_{t-1}+\eta {\nabla }_{\theta }J(\theta -\gamma V_{t-1}) \\ \theta =\theta -v_t \end{gathered}$$
**pros: ** 当梯度方向快要改变的时候，它提前获得了该信息，从而减弱了这个过程，再次减少了无用的迭代。超参数设定值: 一般 γ 仍取值 0.9 左右

自适应梯度下降法（Adagrad）

其可以对低频的参数做较大的更新，对高频的做较小的更新对于稀疏的数据它的表现很好，很好地提高了 SGD 的鲁棒性；

$${\theta }_{t+1,i}={\theta }_{t,i}-\frac{\eta }{\sqrt{G_{t,ii}+ϵ}}\cdot g_{t,i}$$
其中g为t时刻参数θ_i的梯度，Gt是个对角矩阵，(i,i)元素就是t时刻参数 ${\theta }_i$的梯度平方和Gii, Gt = Gt-1 + Gii

**pros: **
减少了学习率的手动调节。超参数设定值：一般η选取0.01。

**cons: **
分母会不断积累，这样学习率就会收缩并最终会变得非常小

改进的自适应梯度下降法（Adadelta）

与Adagrad相比，就是分母的 G 换成了过去的梯度平方的衰减平均值，指数衰减平均值
$$\delta {\theta }_t=-\frac{\eta }{\sqrt{E[g^2{]}_t+ϵ}}\cdot g_t$$
这个分母相当于梯度的均方根 root mean squared (RMS)，在数据统计分析中，将所有值平方求和，求其均值，再开平方，就得到均方根值。其中 E 的计算公式如下，t 时刻的依赖于前一时刻的平均和当前的梯度：
$$E[g^2{]}_t=\gamma E[g^2{]}_{t-1}+(1-\gamma )g_t^2$$
此外，还可将学习率更换成RMS[\delta \theta], 即第二种方式
$$\begin{gathered} \delta {\theta }_t=-\frac{\sqrt{E[g^2{]}_{t-1}+ϵ}}{\sqrt{E[g^2{]}_t+ϵ}}\cdot g_t \\ {\theta }_{t+1}={\theta }_t+\delta {\theta }_t \end{gathered}$$

均方梯度下降法（RMSprop）

RMSprop 和 Adadelta 都是为了解决 Adagrad 学习率急剧下降问题的。
与Adadelta 的第一种形式相同：
超参数设定值:Hinton 建议设定 γ 为 0.9, 学习率 η 为 0.001。

**pros: ** 减少了摆动，允许一个更大的学习率

Adaptive Moment Estimation梯度下降法（Adam）

随机梯度下降保持单一的学习率（即 alpha）更新所有的权重，学习率在训练过程中并不会改变。而 Adam 通过计算梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应性学习率。这个算法是另一种计算每个参数的自适应学习率的方法，相当于 RMSprop + Momentum。

除了像 Adadelta 和 RMSprop 一样存储了过去梯度的平方 vt 的指数衰减平均值 ，也像 momentum 一样保持了过去梯度 mt 的指数衰减平均值：
$$\begin{gathered} m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)g_t \\ {v}_t={\beta }_2{v}_{t-1}+(1-{\beta }_2)g_t^2 \end{gathered}$$
如果mt和vt被初始化为0向量，那它们就会向0偏置，所以做了偏差校正，通过计算偏差校正后的mt和vt来抵消这些偏差:
$$\begin{gathered} \widehat{m_t}=\frac{m_t}{1-{\beta }_1^t} \\ \widehat{v_t}=\frac{v_t}{1-{\beta }_2^t} \end{gathered}$$
梯度更新规则:
$${\theta }_{t+1}={\theta }_t-\frac{\eta }{\sqrt{\widehat{v_t}}+ϵ}\widehat{m_t}$$
超参数设定值:建议 β1 ＝ 0.9，β2 ＝ 0.999，ϵ ＝ 10e−8。
实践表明，Adam 比其他适应性学习方法效果要好。
Adam 和 SGD 区别：Adam = Adaptive + Momentum，顾名思义Adam集成了SGD的一阶动量和RMSProp的二阶动量。

3. 牛顿法

利用二阶导数，收敛速度快；但对目标函数有严格要求，必须有连续的一、二阶偏导数，计算量大。
利用牛顿法求解目标函数的最小值其实是转化成求使目标函数的一阶导为0的参数值。

简述梯度下降法和牛顿法的优缺点？梯度下降法和牛顿法区别

• 牛顿法：是通过求解目标函数的一阶导数为0时的参数，进而求出目标函数最小值时的参数。①收敛速度很快。②海森矩阵的逆在迭代过程中不断减小，可以起到逐步减小步长的效果。③缺点：海森矩阵的逆计算复杂，代价比较大，因此有了拟牛顿法。
• 梯度下降法：是通过梯度方向和步长，直接求解目标函数的最小值时的参数。越接近最优值时，步长应该不断减小，否则会在最优值附近来回震荡。

Normalization

Batch Normalization(批标准化)

标准化使得每层网络的输入都服从（0，1）正态分布。

前向传播代码:

def batchnorm_forward(x, gamma, beta, eps):
  N, D = x.shape
  #为了后向传播求导方便，这里都是分步进行的
  #step1: 计算均值
  mu = 1./N * np.sum(x, axis = 0)
  #step2: 减均值
  xmu = x - mu
  #step3: 计算方差
  sq = xmu ** 2
  var = 1./N * np.sum(sq, axis = 0)
  #step4: 计算分母项即 1/std_var
  sqrtvar = np.sqrt(var + eps)	
  ivar = 1./sqrtvar
  #step5: normalization->x^
  xhat = xmu * ivar
  #step6: scale and shift
  gammax = gamma * xhat
  out = gammax + beta
  #存储中间变量
  cache = (xhat,gamma,xmu,ivar,sqrtvar,var,eps)
  return out, cache

反向传播代码:

def batchnorm_backward(dout, cache):
  #解压中间变量
  xhat,gamma,xmu,ivar,sqrtvar,var,eps = cache
  N,D = dout.shape
  #step6
  dbeta = np.sum(dout, axis=0)
  dgammax = dout
  dgamma = np.sum(dgammax*xhat, axis=0)
  dxhat = dgammax * gamma
  #step5
  divar = np.sum(dxhat*xmu, axis=0)
  dxmu1 = dxhat * ivar #注意这是xmu的一个支路
  #step4
  dsqrtvar = -1. /(sqrtvar**2) * divar
  dvar = 0.5 * 1. /np.sqrt(var+eps) * dsqrtvar
  #step3
  dsq = 1. /N * np.ones((N,D)) * dvar
  dxmu2 = 2 * xmu * dsq #注意这是xmu的第二个支路
  #step2
  dx1 = (dxmu1 + dxmu2) 注意这是x的一个支路
  #step1
  dmu = -1 * np.sum(dxmu1+dxmu2, axis=0)
  dx2 = 1. /N * np.ones((N,D)) * dmu 注意这是x的第二个支路
  #step0 done!
  dx = dx1 + dx2
  return dx, dgamma, dbeta

batchnorm的几个参数，可学习的参数有哪些？
参数γ和β，即缩放参数和平移参数。

Batch Normalization的作用

• 解决了每批数据训练时的不规则分布给训练造成的困难，对批数据进行规范化，还可以在梯度反传时，解决梯度消失的问题。也是一种正则方法，可以代替其他正则方式如dropout，但通过这样的正则化，也消融了数据之间的许多差异信息。
• 提升了训练速度，收敛过程大大加快；增加分类效果；对于初始化要求没那么高。

Batch Normalization一般用在网络的哪个部分啊
卷积层+池化层+BN层+激活层

Batch Normalization为什么要重构
引入了这个可学习重构参数γ、β，让我们的网络可以学习恢复出原始网络所要学习的特征分布

• 目前在实践上，倾向于把BN放在ReLU后面。也有评测表明BN放ReLU后面效果更好

Batch Normalization, Group Normalization, Instance Normalization, Layer Normalization

1. Batch Normalization
   对Batch维度进行计算；则会生成 一 个 variance, mean。
   pros
   BN使得网络中每层输入数据的分布相对稳定，加速模型学习速度；
   BN使得模型对网络中的参数不那么敏感，简化调参过程，使得网络学习更加稳定；
   BN允许网络使用饱和性激活函数（例如sigmoid，tanh等），缓解梯度消失问题；
   BN具有一定的正则化效果
   cons
   受限于Batch size,检测任务中超分辨率时batch size=1 or 2；
   训练集与测试集的分布存在差异

2. Group Normalization
   将 Channels 划分为多个 groups，再计算每个 group 内的均值和方法，以进行归一化,与Batch Size无关。则会生成batch size *Group个 variance mean。

3. Instance Normalization
   仅仅对每一个图片的每一个通道最归一化；则会生成 batch size * channels个 variance mean。

4. Layer Normalization
   对一个特征图的所有通道做归一化；则会生成 batch size 个 variance mean。

   G=1: Layer Normalization
   G=C: Instance Normalization

基础卷积神经网络

1. CNN的经典模型
LeNet，AlexNet，VGG，GoogLeNet，ResNet，DenseNet
2. CNN层和全连接层有什么区别？
全连接层：一个是直接矩阵乘法映射输出结果。CNN是通过卷积核(小尺寸的矩阵)滑动计算出结果。
3. CNN的特点以及要求？ — translation equivariance and locality

• 共享参数，局部连接
• 需要输入数据分布一致

4. Resnet相比于之前的卷积神经网络模型中，最大的改进点是什么？
增加了Residual block（即跳跃连接）和 bottleneck层；resnet是一个拟合残差的结构，indentity mapping，这样网络学习任务更简单，可以有效地解决梯度弥散问题。

5. Resnet为啥能解决梯度消失？
由于每做一次卷积（包括对应的激活操作）都会浪费掉一些信息：比如卷积核参数的随机性（盲目性）、激活函数的抑制作用等等。shortcut起到了减损的效果。

6. resnet第二个版本做了哪些改进？

Resnetv2：

1. 相比于原始的网络结构，先激活的网络中f是恒等变换（即addition后没有再加Relu层），这使得模型优化更加容易
2. 使用了bn+relu作为预激活层，加强了正则化，即能够减少网络过拟合
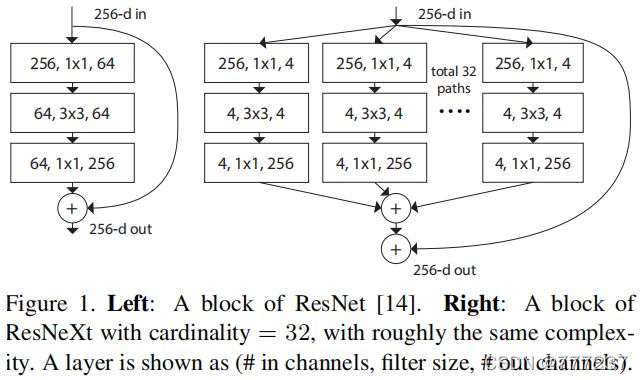
   ***Resnet性能最好的变体是Resnext***

ResNeXt是基于Resnet与Inception的Split, Transfrom, Concat思想的结合体。可分离的思想。即先将输入切分到不同的低维度中，然后做一个特征映射，最后将结果融合到一起。
ResNeXt提出了一个基数（cardinatity）的概念，用于作为模型复杂度的另外一个度量。基数（cardinatity）指的是一个block中所具有的相同分支的数目。

7.简述InceptionV1到V4的网络、区别、改进？

• Inceptionv1的核心就是把googlenet的某一些大的卷积层换成11, 33, 5*5的小卷积，这样能够大大的减小权值参数数量。

• inception V2在输入的时候增加了batch_normal，所以他的论文名字也是叫batch_normal，加了这个以后训练起来收敛更快，学习起来自然更高效，可以减少dropout的使用， 将3×3 卷积继续分解为3 × 1卷积和1 × 3卷积。

  — 探索了Factorization into smaller convolutions，Spatial Factorization into Asymmetric Convolutions，Made wider instead of deeper以及Efficient Grid Size Reduction

• inception V3把googlenet里一些77的卷积变成了17和71的两层串联，33的也一样，变成了13和31，这样加速了计算，还增加了网络的非线性，减小过拟合的概率。另外，网络的输入从224改成了299.

  — 提出Utility of Auxiliary 和 Classifiers Label Smoothing模型正则，探索了Spatial Factorization into Asymmetric Convolutions

• inception v4实际上是把原来的inception加上了resnet的方法，从一个节点能够跳过一些节点直接连入之后的一些节点，并且残差也跟着过去一个。另外就是V4把一个先1×1再3×3那步换成了先3×3再1×1

8.DenseNet为什么比ResNet有更强的表达能力？
DenseNet在增加深度的同时，加宽每一个DenseBlock的网络宽度，能够增加网络识别特征的能力，而且由于DenseBlock的横向结构类似 Inception block的结构，使得需要计算的参数量大大降低。

损失函数

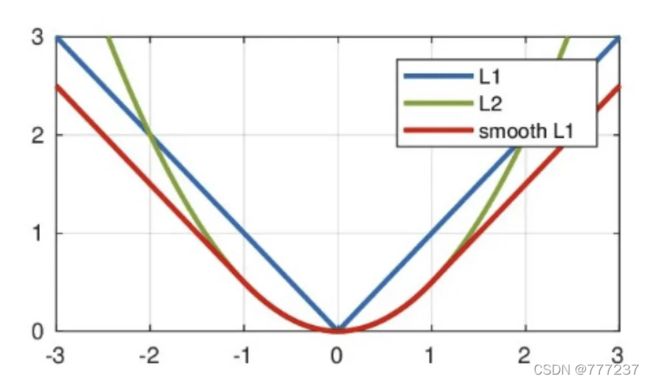
1. 说一下smooth L1 Loss,并阐述使用smooth L1 Loss的优点

$$\begin{gathered} L1=|y-\hat{y}| \\ L2=|y-\hat{y}{|}^2 \\ smoot{h}_{L1}=\{\begin{array}{ll}0.5L{1}^2& if|L1|<1\\ |L1|-0.5& ohterwise\end{array} \end{gathered}$$

L1-Loss 在0点出导数不唯一即连续不可导，会造成收敛不稳定
smooth L1-Loss的优点：
1. 相比于L1 Loss，可以更快的收敛。
2. 相比于L2-Loss，
L2-Loss 会出现离群点outliers，则此时导致梯度很大。
因此faster-Rcnn 选择使用更加平稳的smooth L1 Loss。

• L1 正则化：增加了所有权重w参数的绝对值之和，逼迫更多的w为0，也就是变稀疏。
  — 服从laplace分布求解的目标函数等价于L1正则项
• L2 正则化：增加了所有权重w参数的平方之和， 逼迫所有w趋向于0但是不为0，(l2的导数为0，变平稳/平滑)
  — 服从Gaussian分布求解的目标函数等价于L2正则项

2.为何分类问题用交叉熵而不用平方损失？什么是交叉熵
Cross-Entropy Loss(CE):
$$\begin{gathered} L(P)=\sum _{c=1}^M-Ylog(P) \\ P=\text{softmax(x) or sigmoid(x)} \end{gathered}$$
Binary Cross-Entropy Loss(BCE):
$$\begin{gathered} f(s_i)=\frac{1}{1+e^{-s_i}} \\ L(P)=-Y_0\cdot log(f(s_0))-(1-Y_0)\cdot log(1-f(s_0)) \end{gathered}$$

• 用平方误差损失函数，误差增大参数的梯度会增大，但是当误差很大时，参数的梯度就会又减小了
  分类中为什么交叉熵损失函数比均方误差损失函数更常用？
  均方误差损失函数适合用在回归任务中，由于常用的sigmoid/tanh等激活函数存在梯度饱和区，使得MSE对权重的梯度会很小，参数w调整的慢，训练也慢，而交叉熵损失函数则不会出现此问题。

3.一张图片多个类别怎么设计损失函数，多标签分类问题

• 二分类 sigmoid函数 二分类交叉熵损失函数（binary_crossentropy）

• 多分类 Softmax函数 多类别交叉熵损失函数（categorical_crossentropy）

• 多标签分类 sigmoid函数 二分类交叉熵损失函数（binary_crossentropy）

4. LR的损失函数？它的导数是啥？加了正则化之后它的导数又是啥？
Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题， LR的损失函数为交叉熵损失函数。

数据类问题

1.样本不平衡的处理方法

1. 欠采样 — 观测类别数量上比例差额大，采样的该类别数量占少数，称为欠采样
2. 过采样
3. 合成采样(SMOTE-synthetic minority oversampling technique) — 对少数类样本进行分析并根据少数类样本人工合成新样本添加到数据集中
4. 在loss方面，采用focal loss等loss进行控制不平衡样本

不平衡类别会造成问题有两个主要原因：1.对于不平衡类别，我们不能得到实时的最优结果，因为模型/算法从来没有充分地考察隐含类。2.它对验证和测试样本的获取造成了一个问题，因为在一些类观测极少的情况下，很难在类中有代表性。

2.讲下数据增强有哪些方法

翻转，旋转，缩放, 裁剪，平移，添加噪声;

cutout，mixup, cutmix, 上下采样, 增加不同惩罚

3.过拟合的解决办法

数据扩充/数据增强/更换简单网络/正则化/dropout/batch normalization

集成学习以及early stopping

**什么是过拟合overfitting：**由于训练时，复杂的模型将抽样误差也考虑在内，对抽样误差进行了很好的拟合。

其根本原因：观测值与真实值存在偏差，训练数据不足，，导致无法描述问题的真实分布，或是模型太过于复杂。

**什么是欠拟合unoverfitting：**训练时简单模型拟合能力差，测试时也同样。

其根本原因：模型太过于简单。

正则化

**正则化原理：**在损失函数上加上某些规则（限制），缩小解空间，从而减少过拟合的可能性。

1. L0、L1、L2正则化

L0 范数：向量中非0元素的个数。

L1 范数 (Lasso Regularization)：向量中各个元素绝对值的和。

L2 范数(Ridge Regression)：向量中各元素平方和再求平方根

2. L1、L2正则化区别，为什么稀疏的解好？

L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。

实现参数的稀疏有什么好处吗？

​ 简化模型，避免过拟合；参数变少使得整个模型获得更好的解释性。

3.正则化有哪几种，分别有什么作用？

L0 范数和 L1 范数都能够达到使参数稀疏的目的，但 L0 范数更难优化求解，L1 范数是 L0 范数的最优凸近似，而且它比 L0 范数要容易优化求解。L1可以用于特征选择。

L2 范数不但可以防止过拟合，提高模型的泛化能力，平稳优化，还可以让我们的优化求解变得稳定和快速。

但L2 范数对大数值和outlier (离群值)更敏感。

激活函数与梯度

• 1.激活函数的意义如下

①模拟生物神经元特性，接受输入后通过一个阈值模拟神经元的激活和兴奋并产生输出；

②为神经网络引入非线性，增强神经网络的表达能力；

③导出神经网络最后的结果(在输出层时)。

常用的激活函数？sigmoid，tanh，ReLU, leaky ReLU, PReLU, ELU，random ReLU等。

• sigmoid

$$\begin{gathered} Sigmoid(x)=\frac{1}{1+e^{-x}} \\ \text{Sigmoid 的导数:}{f}^{\prime }(x)=f(x)[1-f(x)] \end{gathered}$$

其值域为(0, 1)，引入了非线性。

但两侧存在***饱和区***，反向传播时会导致梯度弥散和梯度爆炸；sigmoid不是***0均值（zero-centered）***；式中有***幂函数***，求解导数耗时。

---

• relu

$$Relu(x)=max(0,x)$$

线性整流单元
pros：
1）解决了gradient vanishing问题 (在正区间)
2）计算速度非常快，只需要判断输入是否大于0
3）收敛速度远快于sigmoid和tanh
cons： 对于小于0的这部分值，这部分神经元不会被激活。

• tanh

$$Tanh(x)=\frac{1-e^{-x}}{1+e^{-x}}$$

双曲正切函数，其域值（-1，1）而且是***zero-centered***

但也存在梯度弥散问题

• leaky relu

$$\begin{gathered} Leak{y}_{R}elu=max(0,x)+\alpha \ast min(0,x) \\ \alpha \text{ – is small constant} \end{gathered}$$

α一般设为一个较小的正数如0.01或0.001
这样就将小于0部分的梯度从零提高到α，给了这些被抑制部分一定参与网络训练的可能。

• PRelu

$$PRelu=max(0,x)+\alpha \ast min(0,x)$$

参数化ReLu（Parameterised ReLu,PReLu）的形式和Leaky ReLu一样，唯一地不同是它将α视作一个可训练的参数而不是人为设定的超参数。这样，就避免了Leaky ReLu中的选定α值的问题。

• relu6

$$Relu6(x)=\{\begin{array}{ll}0& \text{if }x\le 0\\ x& \text{if }0<n<6\\ 6& \text{if }n\ge 6\end{array}$$

• Softplus

$$Softplus(x)=ln(1+e^x)$$

• swish

$$Swish(x)=\frac{x}{1+e^{-x}}$$

• mish

$$Mish(x)=x\ast tanh(ln(1+e^{-x}))$$

• 多个sigmoid与一个softmax都可以进行多分类.如果多个类别之间是互斥的，就应该使用softmax，即这个东西只可能是几个类别中的一种。如果多个类别之间不是互斥的，使用多个sigmoid。
  用softmax做分类函数，假如现在要对1w甚至10w类做分类会出现什么问题？
  过拟合。early-stopping / triplet-loss / hard-example

• 2.梯度消失/爆炸是什么？
  反向传播中由于链式求导法则的连乘，如果乘数都比较小趋于0，最终传递到网络输入层的梯度会变得很小（梯度消失），如果乘数都很大，最终的梯度也会变得很大（梯度爆炸），其实二者都是因为网络太深导致权值更新不稳定，本质上是因为梯度反向传播中的连乘效应。

回归

• 1.分类和回归的区别，各举例3个模型
  定量输出称为回归，或者说是连续变量预测；定性输出称为分类，或者说是离散变量预测。
  常见分类模型有感知机、朴素贝叶斯、逻辑回归（LR）、支持向量机（SVM）等；
  常见回归模型有线性回归、多项式回归、岭回归（L2正则化）、Lasso回归（L1正则化）,Ridge回归（L2正则化 ）等；

• 2.线性回归和逻辑回归的区别
  区别：LR通常用于二分类，使用的是交叉熵损失函数；线性回归用于回归，使用的是均方误差损失函数。

• 3.怎么优化LR和求解LR
  梯度下降，极大似然法

SVM—支持向量机

支持向量机（support vector machines, SVM）是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；SVM还包括核技巧，这使它成为实质上的非线性分类器。SVM的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题，也等价于正则化的合页损失函数的最小化问题。SVM的的学习算法就是求解凸二次规划的最优化算法。

1. SVM的原理

SVM学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。
$$w\cdot x+b=0$$
即为分离超平面，对于线性可分的数据集来说，这样的超平面有无穷多个（即感知机），但是几何间隔最大的分离超平面却是唯一的。

2. SVM的核函数了解哪些？为什么要用核函数？

当样本在原始空间线性不可分时，可将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。

①线性核函数
$$k(x,x_i)=x\cdot x_i$$
线性核，主要用于线性可分的情况，我们可以看到特征空间到输入空间的维度是一样的，其参数少速度快，对于线性可分数据，其分类效果很理想

②多项式核函数
$$k(x,x_i)=((x\cdot x_i)+1{)}^d$$
多项式核函数可以实现将低维的输入空间映射到高纬的特征空间，但是多项式核函数的参数多，当多项式的阶数比较高的时候，核矩阵的元素值将趋于无穷大或者无穷小，计算复杂度会大到无法计算。

③高斯（RBF）核函数
$$k(x,x_i)=exp(-\frac{|x-x_i{|}^2}{{\delta }^2})$$
高斯径向基函数是一种局部性强的核函数，其可以将一个样本映射到一个更高维的空间内，该核函数是应用最广的一个，无论大样本还是小样本都有比较好的性能，而且其相对于多项式核函数参数要少，因此大多数情况下在不知道用什么核函数的时候，优先使用高斯核函数。

④sigmoid核函数

$$k(x,x_i)=tanh(\eta <x,x_i>+\theta )$$
采用sigmoid核函数，支持向量机实现的就是一种多层神经网络。

如果特征的数量大到和样本数量差不多，则选用LR或者线性核的SVM；

如果特征的数量小，样本的数量正常，则选用SVM+高斯核函数；

如果特征的数量小，而样本的数量很大，则需要手工添加一些特征从而变成第一种情况。

3. SVM如何解决线性不可分问题？

间隔最大化，通过引入软间隔、核函数解决线性不可分问题。

4. SVM优化的目标是啥？SVM的损失函数，SVM的适用场景

凸优化问题，
$$\begin{gathered} mi{n}_{v,b}=\frac{1}{2}|w{|}^q \\ s.t.y_i(w^T{x}_i+b)\ge 1 \end{gathered}$$
SVM的损失函数就是合页损失函数加上正则化项；
$$\sum _i^N[1-y_i(w^T{x}_i+b){]}_{+}+\lambda |w{|}^2$$
5. SVM为什么要对偶(优化复杂度转变，核化)

①首先是我们有不等式约束方程，这就需要我们写成min max的形式来得到最优解。而这种写成这种形式对x不能求导，所以我们需要转换成max min的形式，这时候，x就在里面了，这样就能对x求导了。而为了满足这种对偶变换成立，就需要满足KKT条件（KKT条件是原问题与对偶问题等价的必要条件，当原问题是凸优化问题时，变为充要条件）。

②对偶问题将原始问题中的约束转为了对偶问题中的等式约束

③方便核函数的引入

④改变了问题的复杂度。由求特征向量w转化为求比例系数a，在原始问题下，求解的复杂度与样本的维度有关，即w的维度。在对偶问题下，只与样本数量有关。

6. LR和SVM介绍+区别，什么场景用SVM比较好

相同点：第一，LR和SVM都是分类算法；第二，如果不考虑核函数，LR和SVM都是线性分类算法，也就是说他们的分类决策面都是线性的。第三，LR和SVM都是监督学习算法。第四，LR和SVM都是判别模型。

不同点： 第一，本质上是其损失函数（loss function）不同。注：lr的损失函数是 cross entropy loss，adaboost的损失函数是expotional loss ,svm是hinge loss，常见的回归模型通常用 均方误差 loss。第二，支持向量机只考虑局部的边界线附近的点，而逻辑回归考虑全局（远离的点对边界线的确定也起作用）。第三，在解决非线性问题时，支持向量机采用核函数的机制，而LR通常不采用核函数的方法。第四，线性SVM依赖数据表达的距离测度，所以需要对数据先做normalization，LR不受其影响。第五，SVM的损失函数就自带正则！而LR必须另外在损失函数上添加正则项。

SVM(支持向量机)主要用于分类问题,主要的应用场景有字符识别、面部识别、行人检测、文本分类等领域。

7.支持向量回归原理(SVR)

SVR（支持向量回归）是SVM（支持向量机）中的一个重要的应用分支。SVR回归与SVM分类的区别在于，SVR的样本点最终只有一类，它所寻求的最优超平面不是SVM那样使两类或多类样本点分的“最开”，而是使所有的样本点离着超平面的总偏差最小。

K-Means(K均值)

K-Means是聚类算法中的最常用的一种，算法最大的特点是简单，好理解，运算速度快，但是只能应用于连续型的数据，并且一定要在聚类前需要手工指定要分成几类。

[选择K个点作为初始质心 
repeat 
    将每个点指派到最近的质心，形成K个簇 
    重新计算每个簇的质心 
until 簇不发生变化或达到最大迭代次数 ]

K-mean ++ 改进了初始化方式

1.K-means聚类的原理以及过程？
K-means算法是很典型的基于距离的聚类算法，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。该算法认为簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。

2.K-means聚类怎么衡量相似度的？
欧式距离

3.K值怎么来进行确定？
轮廓系数法和手肘法

4.简要阐述一下KNN算法和K-Means算法的区别

• KNN算法是分类算法，分类算法肯定是需要有学习语料，然后通过学习语料的学习之后的模板来匹配我们的测试语料集，将测试语料集合进行按照预先学习的语料模板来分类；
• Kmeans算法是聚类算法，聚类算法与分类算法最大的区别是聚类算法没有学习语料集合。

机器学习相关常考内容

• To be continued