【论文笔记】Beyond Self-attention: External Attention using Two Linear Layers for Visual Tasks

论文

论文题目：Beyond Self-attention: External Attention using Two Linear Layers for Visual Tasks

投递：CVPR 2021

论文地址：https://arxiv.org/abs/2105.02358

项目地址：https://github.com/MenghaoGuo/EANet

论文翻译：Beyond Self-attention: External Attention using Two Linear Layers for Visual Tasks - 1 - 论文学习 - 慢行厚积 - 博客园

论文解释：论文笔记《Beyond Self-attention: External Attention using Two Linear Layers for Visual Tasks》 - Liuyangcode - 博客园

主要解决的Self-Attention(SA)的两个痛点问题：（1）O(n^2)的计算复杂度；(2)SA是在同一个样本上根据不同位置计算Attention，忽略了不同样本之间的联系。因此，本文采用了两个串联的MLP结构作为memory units，使得计算复杂度降低到了O(n)；此外，这两个memory units是基于全部的训练数据学习的，因此也隐式的考虑了不同样本之间的联系。

Abstract

注意力机制，特别是自注意力机制，在视觉领域中的深度特征表示扮演重要角色。在自注意力机制中，特征图每个位置的更新都是使用计算特征图的加权和得到的，这个权重来源于所有位置中的成对关联，自注意力机制的长程依赖得以建立，但是自注意力机制有平方的复杂度以及对不同特征图之间的潜在关联的忽略。本文提出一个叫外部注意力的新的注意力机制。该注意力机制是外部的，小的，可学习的以及共享内存。易于实现，使用两个线性层和归一化层BN就行，可以方便替代现有方法的自注意力机制。外部注意力具有线性的复杂度和隐式地考虑了不同特征图之间的关系。论文进一步将多头机制融入到外部注意力中，为图像分类提供一个全MLP架构，即外部注意力MLP（external attention MLP，EAMLP）。

Introduction

• 本文提出了一种新的轻量级注意机制——外部注意力(external attention，见图1c)。如图1a)所示，计算自注意力需要首先通过计算self query vectors和self key vectors之间的亲和度来计算一个attention map，然后通过该attention map对self value vectors进行加权来生成一个新的特征图feature map。计算复杂度：
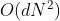
• （本文）外部注意力的工作原理是不同的。首先通过计算self query vectors与一个external learnable key memory之间的亲和度来计算 attentionmap，然后通过将该attention map与另一个external learnable value memory相乘来得到一个精细的特征图 featuremap。计算复杂度是O(dSN)；d和S是超参数，该算法在像素数上是线性的。
• 两个memory通过线性层的方式实现，独立于单个样本，并且在整个数据集中共享参数，具有强大的正则作用并且提高了注意力的泛化机制。其之所以轻量化的核心在于memory中的元素数量比输入特征中少很多，只具有线性复杂度。这个额外的memory设计来学习整个数据集上最有区分度的特征，捕获最有信息的部分

结构图

METHODOLOGY

实现简单，只需使用两个线性层和两个归一化层。伪代码如下：

Self-Attention 自注意力

自注意力机制(可见图1a)。给定一个输入特征map： 

 ，其中N是元素数量（或图像像素数量），d是特征维度数，自注意力线性投射输入为一个query矩阵、一个key矩阵和一个value矩阵。自注意力公式为：

其中，是注意力矩阵，是第i个和第j个元素的成对亲和度值。

自注意力的一个常用简化版变体（图1b）直接从输入特征F 计算了一个注意力map，公式如下：

这里通过在特征空间中计算像素级相似度得到注意力map，输出是输入的精细化特征表征。

计算复杂度：

常见办法是利用对patches而不是像素的自注意力来减少计算工作量。

自注意力可以看作是self values的线性组合来细化输入特征。然而，在这个线性组合中，是否真的需要N × N的自注意矩阵和N个元素的self value矩阵，这一点并不明显。此外，自注意力只考虑了数据样本中元素之间的关系，而忽略了不同样本中元素之间的潜在关系，潜在地限制了自注意力的能力和灵活性。

External Attention 外部注意力 

因此，论文提出新的注意力模块，命名为外部注意力（external attention），用于计算输入像素和一个external memory单元的注意力，公式为：

和自注意力不同，等式(5)中的是第i个像素和M第j行的相似度，其中M是一个独立于输入的可学习参数，其作为整个训练数据集的memory。A是从该已学好的dataset-level先验知识推导得到的注意力map；以相同的方法归一化为自注意力（可见3.2节）。最后,我们通过A的相似度更新M的输入特性。

实际上，使用两个不同的memory单元和作为key和value，去增强网络的能力。因此外部注意力的计算变为：

外部注意力的计算复杂度是O(dSN)；d和S是超参数，该算法在像素数上是线性的。

实验发现一个小的S，如64，就能在实验中得到好效果。因此，外部注意力是比自注意力高效的，允许其直接应用到大尺度输入中。还注意到外部注意力的计算负载粗略等价于1x1卷积。

Normalization

自注意力中使用Softmax去归一化注意力map，因此。然而，注意力map是通过矩阵乘法计算出来的。与余弦相似度不同，注意力map对输入特征的scale非常敏感。为了避免这个问题，论文选用double-normalization，它分别归一化列和行。这种double-normalization 公式为:

Multi-head external attention 多头外部注意力

自注意力在不同的输入channels上计算多次，这称为multi-head注意力。multi-head注意力可以捕获tokens之间的不同关系，提高了single head注意力的能力。

多头外部注意力，伪代码：

 多头外部注意力，架构图：

multi-head外部注意力可以写成:

其中hi是第i个head，H是heads的数量，Wo是一个用来保持输入输出维度一致的线性转换矩阵。

和是不同heads共享的memory单元。

这种架构的灵活性允许我们在共享memory单元中平衡head H的数量和元素S的数量。

EXPERIMENTS

文章中做了多个实验来证明其有效性，包括分类、分割、目标检测、图像生成，点云等等，从结果来看确实是有效的。具体请看论文。

EANet ，用于语义分割。

数据集：PASCAL VOC

网络主干： FCN

batch size和总迭代次数分别设置为12和30000次。

• SA：self-attention；EA：external attention。
• S：memory单元中的元素数量；OS：主干网络的输出步幅stride。
• FCN：全卷积网络；Sofrmax、DoubleNorm：标准化方式。

Computational requirements

关于输入大小的线性复杂度带来了效率上的显著优势。我们在输入大小为1 × 512 × 128 × 128的情况下，将外部注意力(EA)模块与标准自注意力(SA)及其几个变体在参数数量和推理操作方面进行了比较，结果如表12所示。外部注意力只需要自注意力所需参数的一半，而且速度要快32倍。与最好的变体相比，外部注意力的速度仍然是前者的两倍。

Visual analysis

Image classification

Object detection and instance segmentation

 Semantic segmentation

Image generation

 Point cloud segmentation

 Point cloud classification

CONCLUSIONS

本文提出了一种新型的、轻量级的、有效的、适用于各种视觉任务的注意机制——外部注意力。外部注意力所采用的两个外部memory单元可以看作是整个数据集的字典，能够学习更多的输入的代表性特征，同时降低计算代价。我们希望外部注意力能够激发它在其他领域的实际应用和研究，比如自然语言处理。

代码

class External_attention(nn.Module):
    '''
    Arguments:
        c (int): The input and output channel number. 官方的代码中设为512
    '''
    def __init__(self, c):
        super(External_attention, self).__init__()
        self.conv1 = nn.Conv2d(c, c, 1)
        self.k = 64
        self.linear_0 = nn.Conv1d(c, self.k, 1, bias=False)

        self.linear_1 = nn.Conv1d(self.k, c, 1, bias=False)
        self.linear_1.weight.data = self.linear_0.weight.data.permute(1, 0, 2)        
        
        self.conv2 = nn.Sequential(
            nn.Conv2d(c, c, 1, bias=False),
            norm_layer(c))        
        
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                n = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
                m.weight.data.normal_(0, math.sqrt(2. / n))
            elif isinstance(m, nn.Conv1d):
                n = m.kernel_size[0] * m.out_channels
                m.weight.data.normal_(0, math.sqrt(2. / n))
            elif isinstance(m, _BatchNorm):
                m.weight.data.fill_(1)
                if m.bias is not None:
                    m.bias.data.zero_()
 

    def forward(self, x):
        idn = x
        x = self.conv1(x)

        b, c, h, w = x.size()
        n = h*w
        x = x.view(b, c, h*w)   # b * c * n 

        attn = self.linear_0(x) # b, k, n
        #linear_0是第一个memory unit
        attn = F.softmax(attn, dim=-1) # b, k, n

        attn = attn / (1e-9 + attn.sum(dim=1, keepdim=True)) #  # b, k, n
        
        x = self.linear_1(attn) # b, c, n
        #linear_1是第二个memory unit
        x = x.view(b, c, h, w)
        x = self.conv2(x)
        x = x + idn
        x = F.relu(x)
        return x