【读点论文】Transformer in Transformer 细化图片结构，递归使用transformer。让图片去拟合自然语言处理的操作。

Transformer in Transformer

Abstract

• Transformer是一种新的神经架构，它通过注意机制将输入数据编码为强大的特征。基本上，视觉transformer首先将输入图像分成几个局部小块，然后计算两种表示及其关系。

• 由于自然图像具有高度的复杂性和丰富的细节和颜色信息，因此块划分的粒度不同以挖掘不同尺度和位置上的物体特征。

• 在本文中指出这些局部补丁内部的注意力对于构建高性能的视觉transformer也是必不可少的，并探索了一种新的架构，即transformer中的transformer(TNT)。

• 具体来说，本文将局部小块(如16×16)视为“视觉句子”，并提出将其进一步划分为更小的小块(如4×4)作为“视觉单词”。每个单词的注意力将与给定视觉句子中的其他单词一起计算，计算成本可以忽略不计。

• 单词和句子的特征将被聚合以增强表示能力。在几个基准上的实验证明了所提出的TNT体系结构的有效性，例如，本文模型在ImageNet上获得了81.5%的top-1准确率，这比具有相似计算成本的最先进的视觉转换器高出约1.7%。

• PyTorch代码可在https://github.com/huawei-noah/CV-Backbones,获得，

• MindSpore代码可在https://gitee.com/mindspore/models/tree/master/research/cv/TNT获得。

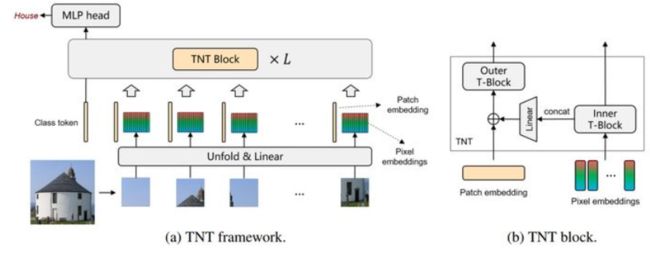
• 提出了一种新颖的Transformer-iN-Transformer（TNT）模型，用于对 patch级和像素级表示进行建模。

• 

  • 在每个TNT块中，外部transformer块用于处理patch嵌入，而内部transformer块则从像素嵌入中提取局部特征。通过线性变换层将像素级特征投影到patch嵌入的空间，然后将其添加到patch中。通过堆叠TNT块，本文建立了用于图像识别的TNT模型。

• 华为诺亚实验室的研究者提出了一种新型视觉 Transformer 网络架构 Transformer in Transformer，它的表现优于谷歌的 ViT 和 Facebook 的 DeiT。TNT 还暗合了 Geoffrey Hinton 最新提出的 part-whole hierarchies 思想。

  • 谷歌 ViT（Vision Transformer）模型是一个用于视觉任务的纯 transformer 经典技术方案。它将输入图片切分为若干个图像块（patch），然后将 patch 用向量来表示，用 transformer 来处理图像 patch 序列，最终的输出做图像识别。但是 ViT 的缺点也十分明显，它将图像切块输入 Transformer，图像块拉直成向量进行处理，因此，图像块内部结构信息被破坏，忽略了图像的特有性质。
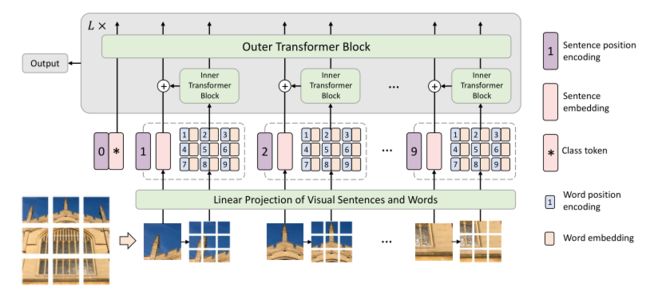
  • 来自华为诺亚实验室的研究者提出一种用于基于结构嵌套的 Transformer 结构，被称为 Transformer-iN-Transformer (TNT) 架构。同样地，TNT 将图像切块，构成 Patch 序列。不过，TNT 不把 Patch 拉直为向量，而是将 Patch 看作像素（组）的序列。
  • 新提出的 TNT block 使用一个外 Transformer block 来对 patch 之间的关系进行建模，用一个内 Transformer block 来对像素之间的关系进行建模。通过 TNT 结构，研究者既保留了 patch 层面的信息提取，又做到了像素层面的信息提取，从而能够显著提升模型对局部结构的建模能力，提升模型的识别效果。

Introduction

• 在过去十年中，计算机视觉(CV)中使用的主流深度神经架构主要建立在卷积神经网络(CNN)上[Alexnet，Resnet，More features from cheap operations]。不同的是，transformer是一种主要基于自注意力机制的神经网络，它可以提供不同特征之间的关系。
• Transformer 是一种主要基于注意力机制的网络结构，能提取输入数据的特征。计算机视觉中的 Transformer 首先将输入图像均分为多个图像块，然后提取器特征和关系。因为图像数据有很多了细节纹理和颜色等信息，所以目前方法所分的图像块的粒度还不够细，以至于难以挖掘不同尺度和位置特征。
• Transformer广泛应用于自然语言处理(NLP)领域，例如著名的BERT和GPT-3模型。这些transformer模型的力量激励整个社区研究transformer在视觉任务中的使用。
• 为了利用transformer架构来执行视觉任务，许多研究人员已经探索了表示来自不同数据的序列信息。例如，Wang等人探索了非局部网络中的自注意力机制[Non-local neural networks]，用于捕获视频和图像识别中的长程相关性。Carion等人提出了DETR，其将对象检测视为直接集预测问题，并使用transformer编码器-解码器架构来解决它。Chen等人提出的iGPT是将纯transfer模型(即没有卷积)通过自监督预训练应用于图像识别的开创性工作。
• 与NLP任务中的数据不同，CV任务中的输入图像和真实标签之间存在语义鸿沟。为此，Dosovitskiy等人开发了ViT【读点论文】AN IMAGE IS WORTH 16X16 WORDS: TRANSFORMERS FOR IMAGE RECOGNITION AT SCALE（ViT）像处理自然语言那样处理图片_羞儿的博客-CSDN博客 ，为迁移基于transformer的NLP模型的成功铺平了道路。具体地说，ViT将给定的图像分割成若干局部小块作为一个视觉序列。然后，可以自然地计算任意两个图像块之间的注意力，以便为识别任务生成有效的特征表示。
• 随后，Touvron等人探索了数据高效的训练和提取，以提高ViT在ImageNet基准上的性能，并获得了大约81.8%的ImageNet top-1准确性，这与最先进的卷积网络的准确性相当。Chen等人进一步将图像处理任务(例如去噪和超分辨率)视为一系列翻译，并开发了用于处理多个低级计算机视觉问题的模型[Pre-trained image processing transformer]。
• 如今，transformer架构已用于越来越多的计算机视觉任务[A survey on vision transformer]，如图像识别，对象检测和分割。
• 虽然上述视觉transformer已经做出了巨大的努力来提高模型的性能，但是大多数现有的工作遵循ViT中使用的传统表示方案，即将输入图像分成小块。这种精致的范式可以有效地捕捉视觉序列信息，并估计不同图像块之间的注意。然而，现代基准中自然图像的多样性非常高，例如，在ImageNet数据集中有超过1.2亿张图像，包含1000个不同的类别。
• 如下图所示，将给定图像表示成局部小块可以帮助研究者找到它们之间的关系和相似性。但是，它们内部也有一些相似度很高的子补丁。因此，本文需要探索一种更精细的视觉图像分割方法来生成视觉序列并提高性能。
  • 
  • Illustration of the proposed Transformer-iN-Transformer (TNT) framework.内部transformer块在同一层中共享。单词位置编码在视觉句子中是共享的。
• 在本文中提出了一种用于视觉识别的新型transformer中transformer(TNT)架构，如上图所示。为了增强视觉transformer的特征表示能力，本文首先将输入图像分成若干块作为“视觉句子”，然后进一步将它们分成子块作为“视觉单词”。
• 除了用于提取视觉句子的特征和注意力的传统transformer块之外，本文还在架构中嵌入了一个子transformer，用于挖掘更小的视觉单词的特征和细节。具体地，使用共享网络独立地计算每个视觉句子中的视觉单词之间的特征和注意力，使得增加的参数和FLOPs(浮点运算)的数量可以忽略不计。
• 然后，将单词的特征聚合到相应的视觉句子中。类别令牌还用于通过全连接头部的后续视觉识别任务。通过提出的TNT模型，本文可以提取细粒度的视觉信息，提供更多细节的特征。
• 然后，本文在ImageNet基准和下游任务上进行了一系列实验，以展示其优越性，并深入分析了大小对划分视觉单词的影响。结果表明，与最先进的transformer网络相比，TNT可以实现更好的精度和FLOPs折衷。
• Transformer 网络推动了诸多自然语言处理任务的进步，而近期 transformer 开始在计算机视觉领域崭露头角。例如，DETR 将目标检测视为一个直接集预测问题，并使用 transformer 编码器 - 解码器架构来解决它；IPT 利用 transformer 在单个模型中处理多个底层视觉任务。与现有主流 CNN 模型（如 ResNet）相比，这些基于 transformer 的模型在视觉任务上也显示出了良好的性能。

Approach

• 本文将描述所提出的transformer中transformer架构，并详细分析计算和参数复杂性。

• Preliminaries

  • 本文先简单描述一下transformer中的基本组件，包括MSA(多头自注意力机制)、MLP(多层感知器)和LN(层归一化)。

  • MSA：在自注意力机制模块中，输入$X\in {\mathbb{R}}^{n\times d}$被线性变换成三个部分，即查询$Q\in {\mathbb{R}}^{n\times d_k}$、关键字$K\in {\mathbb{R}}^{n\times d_k}$和值$V\in {\mathbb{R}}^{n\times d_v}$，其中n是序列长度，$d、d_k、d_v$分别是输入、查询(关键字)和值的维度。缩放的点积注意力应用于Q、K、V:

    • $$Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$

    • 最后，使用线性图层生成输出。多头自注意力机制将查询、键和值拆分为h个部分并并行执行attention函数，然后将每个头的输出值级联并线性投影形成最终输出。

    • 注意力机制（Attention Mechanism）的本质是：对于给定目标，通过生成一个权重系数对输入进行加权求和，来识别输入中哪些特征对于目标是重要的，哪些特征是不重要的；

    • 为了实现注意力机制，可以将输入的原始数据看作< Key, Value>键值对的形式，根据给定的任务目标中的Query 计算 Key 与 Query 之间的相似系数，可以得到Value值对应的权重系数, 之后再用权重系数对 Value 值进行加权求和, 即可得到输出。将注意力权重系数W与Value做**点积操作（加权求和）**得到融合了注意力的输出：

      • $$Attention(Q,K,V)=W\cdot V=softmax(Q{K}^T)\cdot V$$

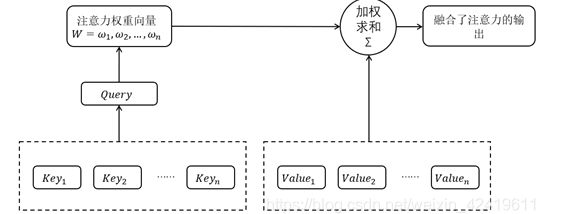
    • 注意力模型的详细结构如下图所示：

      • 
      • 需要注意，如果Value是向量的话，加权求和的过程中是对向量进行加权，最后得到的输出也是一个向量。

    • 注意力机制可以通过对< Key, Query>的计算来形成一个注意力权重向量，然后对Value进行加权求和得到融合了注意力的全新输出，注意力机制在深度学习各个领域都有很多的应用。不过需要注意的是，注意力并不是一个统一的模型，它只是一个机制，在不同的应用领域，Query, Key和Value有不同的来源方式，也就是说不同领域有不同的实现方法。

  • MLP：MLP应用于自注意力层之间，用于特征变换和非线性:$MLP(X)=FC(\sigma (FC(X))、FC(X)=XW+b$.其中W和b分别是全连接层的权重和偏置项，σ()是激活函数如GELU。

    • MLP中文叫法是多层感知机，其实质就是神经网络。MLP中文叫法是多层感知机，其实质就是神经网络。是深度神经网络(DNN)的基础算法,有时候提起DNN就是指MLP。在MLP中,层与层之间是全连接的.

    • GELU激活函数

      • 全称是GAUSSIAN ERROR LINEAR UNIT,高斯误差线性单元,与Sigmoids相比，像ReLU，ELU和PReLU这样的激活可以使神经网络更快更好地收敛。高斯误差线性单元激活函数在最近的 Transformer 模型（谷歌的 BERT 和 OpenAI 的 GPT-2）中得到了应用。GELU 的论文来自 2016 年，但直到最近才引起关注。

      • $GELU(X)=x\ast P(X\le x)=x\ast \varphi (x),x～N(0,1)$.x是输入值，X是具有零均值和单位方差的高斯随机变量。P(X<=x)是X小于或等于给定值x的概率。

      • 想使用它来创建确定性函数以用作激活。 请注意，SOI（zero-or-identity）可以执行以下两项操作之一：以概率 $\varphi (x)$ 做恒等映射，以概率 $1-\varphi (x)$ 映射到0。对应着伯努利分布，该式子的期望（平均值)为：

        • $$\begin{gathered} I\ast x\ast \varphi (x)+0\ast x\ast (1-\varphi (x))=x\ast \varphi (x) \\ 近似计算：GEELU(X)=0.5\ast x\ast (1+tanh[\sqrt{\frac{2}{\pi }}\ast (x+0.044715x^3)]) \\ GELU激活函数的倒数：\frac{dGELU(x)}{dx}=\varphi (x)+x\ast \varphi (x{)}^{‘} \end{gathered}$$

        • 其中$\Phi (x)$指的是x xx的高斯正态分布的累积分布，完整形式如下：$xP(X\le x)=x\ast {\int }_{-\infty }^x\frac{e^{-(x-\mu {)}^2/(2{\delta }^2)}}{\sqrt{2\pi }\delta }dX$,计算的结果约为$0.5\ast x\ast (1+tanh[\sqrt{\frac{2}{\pi }}\ast (x+0.044715x^3)])$。

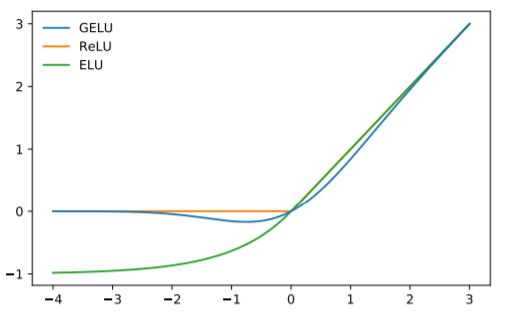
      • Gelu(u(均值)=0,σ(方差) =1),Elu(α = 1),Relu激活函数对比图

        • 

  • LN：层标准化是transformer中稳定训练和更快收敛的关键部分。LN应用于每个样本$x\in {\mathbb{R}}^d$，如下所示:

    • KaTeX parse error: Undefined control sequence: \var at position 19: …(x)=\frac{x-μ}{\̲v̲a̲r̲}\odotγ+β

    • 其中μ∈ R、δ ∈ R分别是特征的平均值和标准偏差，$\odot$是element-wise dot，$\gamma \in {\mathbb{R}}^d、\beta \in {\mathbb{R}}^d$是可学习的仿射变换参数。

• Transformer in Transformer

  • 给定一幅2D图像，本文将其均匀分成n个patch $X=[X1，X2，，Xn]\in {\mathbb{R}}^{n\times p\times p\times 3}$，其中(p，p)是每个图像patch的分辨率。ViT 只是利用一个标准的transformer来处理一系列的补片，这破坏了补片的局部结构。

  • 相反，本文提出transformer中transformer(TNT)架构来学习图像中的全局和局部信息。在TNT中，本文将补丁视为代表图像的视觉句子。每个小块被进一步分成m个子小块，即一个可视句子由一系列可视单词组成:

    • $$X_i\to [x^{i,1},x^{i,2},\cdot \cdot \cdot ,x^{i,m}],$$

    • 其中，$x^{i，j}\in {\mathbb{R}}^{s\times s\times 3}$是第i个可视句子的第j个可视单词，(s，s)是子块的空间大小，j = 1，2，，m。利用线性投影，本文将可视单词转换成单词嵌入序列:

      • $$Y_i=[y^{i,1},y^{i,2},\cdot \cdot \cdot ,y^{i,m}],y^{i,j}=FC(Vec(x^{i,j})),(5)$$

      • 其中$y^{i，j}\in R^c$为第j个单词嵌入，c为单词嵌入的维数，Vec(·)为向量化运算。

    • 在TNT中，本文有两个数据流，其中一个流跨可视句子操作，另一个处理每个句子中的可视单词。对于单词嵌入，本文利用transformer块来探索视觉单词之间的关系:

      • $$\begin{gathered} Y_l^{‘i}=Y_{l-1}^i+MSA(LN(Y_{l-1}^i)),(6) \\ {Y}_l^i=Y_l^{‘i}+MLP(LN(Y_l^{‘i})).(7) \end{gathered}$$

      • 其中l = 1，2，，L是第L个块的索引，L是堆叠块的总数。第一个模块的输入$Y_0^i$就是等式5中的Yi。变换后图像中的所有单词嵌入都是$Y_l=[Y_l^1，Y_l^2，...，Y_l^n]$。这可以视为内部transformer模块，表示为Tin。这个过程通过计算任意两个视觉单词之间的交互来建立视觉单词之间的关系。例如，在一幅人脸图像中，与眼睛相对应的单词与眼睛的其他单词的关联度更高，而与前额部分的交互度较低。

    • 对于句子级，本文创建句子嵌入存储器来存储句子级表示的序列:$Z_0=[Z_{class}，Z_0^1，Z_0^2，...，Z_0^n]\in {\mathbb{R}}^{(n+1)\times d}$其中Zclass是类似于ViT 的cls标记，它们都被初始化为零。在每一层中，通过线性投影将单词嵌入序列转换到句子嵌入域中，并添加到句子嵌入中:$Z_{l-1}^i=Z_{l-1}^i+FC(Vec(Y_l^i)),$。

    • 其中，$Z_{l-1}^i\in {\mathbb{R}}^d$和全连接层FC使尺寸相匹配。通过上述加法运算，句子嵌入的表示通过单词级特征得到增强。本文使用标准transformer块来变换句子嵌入:

      • $$\begin{gathered} Z_l^{‘}=Z_{l-1}+MSA(LN(Z_{l-1})),(9) \\ {Z}_l=Z_l^{‘}+MLP(LN(Z_l^{‘})).(10) \end{gathered}$$

      • 这个外部transformer块Tout用于对句子嵌入之间的关系进行建模。

    • 总之，TNT块的输入和输出包括视觉单词嵌入和句子嵌入，因此TNT可以被公式化为:

      • $$Y_l,Z_l=TNT(Y_{l-1},Z_{l-1}).$$

    • 在本文的TNT块中，内部transformer块用于对视觉单词之间的关系进行建模以进行局部特征提取，外部transformer块从句子序列中捕获内在信息。通过堆叠L次TNT块，本文构建了transformer中transformer网络。最后，分类token用作图像表示，并且全连接层被应用于分类。

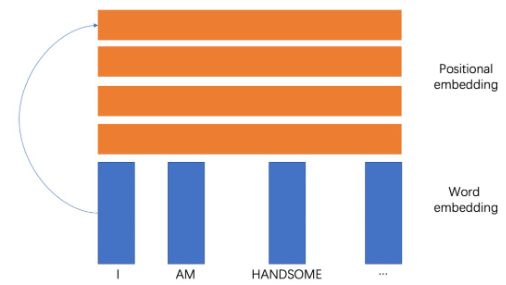
  • Position encoding：空间信息是图像识别中的一个重要因素。对于句子嵌入和单词嵌入，本文都添加了相应的位置编码来保留空间信息。这里使用了标准的可学习的1D位置编码。具体来说，每个句子都分配有一个位置编码:$Z_0\leftarrow Z_0+E_{sentence},$.

    • 其中，$E_{sentence}\in {\mathbb{R}}^{(n+1)\times d}$是句子位置编码。对于句子中的视觉单词，在每个单词嵌入中加入单词位置编码:$Y_0^i\leftarrow Y_0^i+E_{word},i=1,2,\cdot \cdot \cdot ,n$。其中$E_{word}\in {\mathbb{R}}^{m\times c}$是跨句子共享的单词位置编码。这样，句子位置编码可以保持全局空间信息，而单词位置编码用于保持局部相对位置。

• Complexity Analysis

  • 一个标准的transformer块包括两部分，即多头自注意力模块和多层感知器。MSA的FLOPs是$2nd(d_k+d_v)+n^2(d_k+d_v)$，MLP的FLOPs是$2n{d}_{v}r{d}_v$其中r是MLP的隐藏层的维度扩展比。总体而言，标准transformer模块的FLOPs为

    • $$FLOP{s}_T=2nd(d_k+d_v)+n^2(d_k+d_v)+2nd{d}_r.(14)$$

    • 由于r通常设置为4，并且输入、键(query)和值的维度通常设置为相同，因此FLOPs计算可以简化为$FLOP{s}_T=2nd(6d+n)$。

    • 参数的数量可以通过下式获得：$Param{s}_T=12dd$

  • 本文的TNT模块由三部分组成:内部transformer模块Tin、外部transformer模块Tout和线性层。Tin和Tout的计算复杂度分别为2nmc(6c + m)和2nd(6d + n)。线性层具有nmcd的FLOPs。总的来说，TNT模块的FLOPs为：

    • $$FLOP{s}_{TNT}=2nmc(6c+m)+nmcd+2nd(6d+n).$$

    • 类似地，TNT块的参数复杂度计算如下：$Param{s}_{TNT}=12cc+mcd+12dd.$。

  • 尽管本文在TNT模块中增加了两个元件，但增加的FLOPs由于c远小于实际中d和O(m) ≈ O(n)。

  • 例如，在DeiT-S配置中，d = 384，n = 196。本文在TNT-S的结构中相应地设置c = 24，m = 16。从等式15和等式17来看，可以得到FLOPsT = 376M和FLOPsTNT = 429M。TNT模块与标准transformer模块的FLOPs比率约为1.14倍。

  • 类似的，参数比值约为1.08倍。实验表明，在计算和存储开销增加很少的情况下，本文的TNT块可以有效地模拟局部结构信息，并在准确性和复杂性之间取得更好的平衡。

• Network Architecture

  • 本文按照ViT和DeiT 的基本配置构建TNT架构。patch大小设置为16×16。默认情况下，子patch的数量设置为m = 4*4 = 16。其他尺寸值在消融研究中进行评估。如下表所示，TNT网络有三种不同模型大小的变体，即TNT-Ti、TNT-S和TNT-B。它们分别由6.1M、23.8M和65.6M的参数组成。处理一幅224×224图像对应的FLOPs分别为1.4B、5.2B和14.1B。
  • 
  • Variants of our TNT architecture：Ti是微小的意思，S是小的意思，B是Base的意思。FLOPs是为分辨率为224×224的图像计算的。

Experiments

• 在这一节中，本文对视觉基准进行了广泛的实验，以评估所提出的TNT架构的有效性。

• Datasets and Experimental Settings

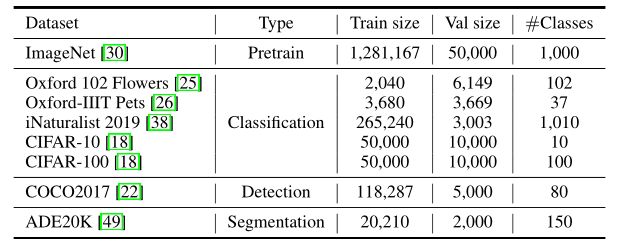
  • 数据集。ImageNet ILSVRC 2012 是一个图像分类基准，由属于1000个类的1.2M训练图像和每类50个图像的50K验证图像组成。本文采用与DeiT中相同的数据扩充策略，包括随机裁剪、随机剪辑、随机扩充、随机擦除、混合和剪切混合。关于ImageNet数据集的许可，请参考http://www.image-net.org/download.
  • 除了ImageNet之外，我们还使用迁移学习在下游任务上进行测试，以评估TNT的泛化能力。下表中列出了所使用的可视化数据集的细节。图像分类数据集的数据扩充策略与ImageNet相同。对于COCO和ADE20K，数据扩充策略遵循PVT的策略。关于这些数据集的许可，请参考原始论文。
    • 
    • 所用可视化数据集的详细信息。
  • 实施细节。本文利用DeiT中提供的训练策略。除了常见设置[resnet]之外，主要的高级技术包括AdamW、标签平滑、DropPath和重复增强。为了更好地理解，本文在下表中列出了超参数。
    • 
    • 除非另有说明，否则本文的方法中使用默认训练超参数。
  • 所有模型都用PyTorch和MindSpore实现，并在NVIDIA Tesla V100 GPUs上训练。潜在的负面社会影响可能包括GPU计算的能耗和二氧化碳排放。

• TNT on ImageNet

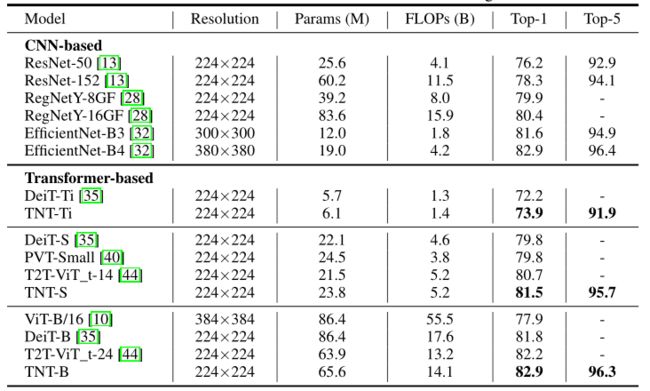
  • 本文使用与DeiT相同的训练设置来训练TNT模型。比较了最近的基于transformer的模型，如ViT和DeiT。为了更好地了解视觉transformer的当前进展，本文还包括了基于CNN的代表性模型，如ResNet、RegNet和EfficientNet。结果如下表所示。
    • 
    • TNT和其他网络在ImageNet上的结果。
  • 通过上表可以看到，本文的基于transformer的模型，即TNT优于所有其他可视化transformer模型。特别是，TNT-S实现了81.5%的top-1准确性，比基线模型DeiTS高1.7%，表明引入的TNT框架有利于保留补片内部的局部结构信息。
  • 与CNN相比，TNT的性能优于广泛使用的ResNet和RegNet。请注意，所有基于transformer的模型仍然不如使用特殊深度卷积的EfficientNet，因此如何使用纯transformer击败EfficientNet仍然是一个挑战。
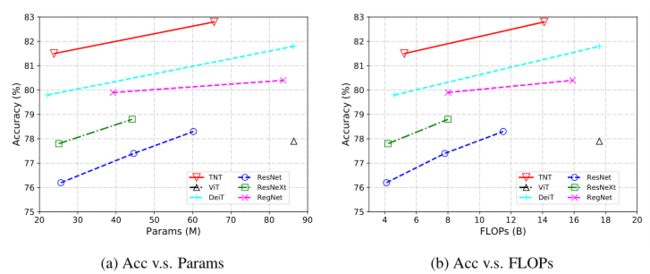
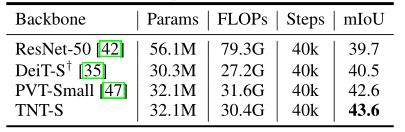
  • 本文还绘制了下图中的精度参数和精度触发器线图，以便直观地比较这些模型。本文的TNT模型始终远远优于其他基于transformer的模型。
    • 
    • ImageNet上典型可视骨干网的性能比较。
  • 推理速度。在设备上部署transformer模型对于实际应用很重要，因此本文测试了TNT模型的推理速度。按照[Training data-efficient image transformers & distillation through attention]，吞吐量是在NVIDIA V100 GPU和PyTorch上测量的，输入大小为224×224。
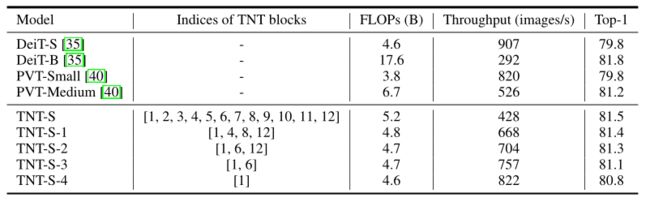
  • 由于小块内的分辨率和内容小于整个图像的分辨率和内容，本文可能需要更少的块来学习它的表示。因此，本文可以减少所用的TNT模块，用普通的transformer模块替换一些。从下表中的结果，可以看到，本文的TNT比DeiT和PVT更有效，在相似的推理速度下实现了更高的准确性。
    • 
    • 视觉transformer模型的GPU吞吐量比较。

• Ablation Studies

  • 位置编码的效果。位置信息对于图像识别非常重要。在TNT结构中，句子位置编码用于保持全局空间信息，单词位置编码用于保持局部相对位置。本文通过分别移除它们来验证它们的效果。如下表所示，可以看到，同时采用补丁位置编码和单词位置编码的TNT-S的性能最好，达到了81.5%的top-1准确率。移除句子/单词位置编码分别导致0.8%/0.7%的准确度下降，而移除所有位置编码会严重降低1.0%的准确度。
  • 
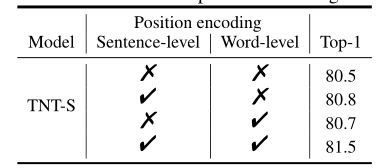
    • Effect of position encoding.
  • Number of heads.。标准transformer中检测头的影响已在多项工作中进行了研究，对于视觉任务，建议头宽度为64。在本文的模型中，本文采用64英寸的外部变压器组头部宽度。内部transformer组中的头数是另一个需要研究的超参数。本文评估了内部transformer块中检测头的效果(下表)。通过表格可以看到，适当数量的头(例如2或4个)可以实现最佳性能。
    • 
    • TNT-S内部transformer组中#头的作用
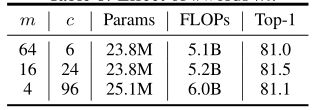
  • Number of visual words ：在TNT中，输入图像被分成多个16×16的小块，并且为了计算效率，每个小块被进一步分成m个子小块(视觉单词)。这里本文测试超参数m对TNT-S架构的影响。当本文改变m时，嵌入维数c也相应地改变以控制触发器。如下表所示，可以看到m的值对性能有轻微的影响，为了提高效率，本文默认使用m = 16，除非另有说明。
    • 
    • #words m的效果。

• Visualization

  • Visualization of Feature Maps：

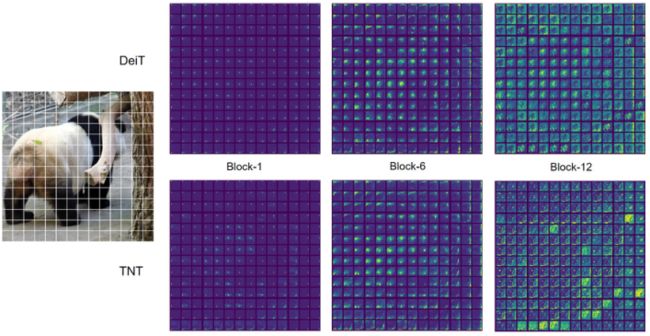
    • 本文将DeiT和TNT的学习特征可视化，以进一步理解所提出的方法的效果。为了更好地显示，输入图像的大小被调整为1024×1024。特征图是通过根据它们的空间位置对嵌块进行整形而形成的。下图(a)中示出了第1、第6和第12块中的特征图，其中为这些块中的每一个随机采样了12个特征图。
    • 
    • DeiT-S和TNT-S特征的可视化。
    • 与DeiT相比，TNT更好地保存了本地信息。本文还使用t-SNE可视化了第12区块的所有384个特征图(上图(b))。通过图像可以看到TNT的特征比DeiT更加多样，包含的信息也更加丰富。这些好处是由于引入了用于模拟局部特征的内部transformer块。
    • 除了patch级特征，本文还在下图中可视化了TNT的像素级嵌入。对于每个小块，本文根据它们的空间位置对单词嵌入进行整形以形成特征图，然后通过信道维度对这些特征图进行平均。对应于14×14块的平均特征图如下图所示。通过下图可以看到，浅层的局部信息保存得很好，随着网络的深入，表示逐渐变得更抽象。
    • 
    • TNT-S平均单词嵌入的可视化。

  • Visualization of Attention Maps

    • 在本文的TNT模块中有两个自注意力层，即内部自注意力和外部自注意力，分别用于建模视觉单词和句子之间的关系。本文在下图中展示了内部transformer中不同query的注意力图。对于给定的查询视觉词，具有相似外观的视觉词的关注值更高，表明它们的特征将与查询更相关地交互。这些相互作用在ViT和DeiT等中被遗漏了。外部transformer中的注意图可以在补充材料中找到。
      • 
      • 内部transformer中不同query的注意图。红色叉号表示查询位置。

• Transfer Learning

  • 为了展示TNT强大的泛化能力，本文将在ImageNet上训练的TNT-S、TNT-B模型转移到下游任务中。

  • Pure Transformer Image Classification.

    • 根据DeiT，本文在4个图像分类数据集上评估了本文的模型，训练集大小从2040到50000幅图像。这些数据集包括上级对象分类(CIFAR-10 ，CIFAR-100 )和细粒度对象分类(牛津-IIIT Pets，牛津102 Flowers 和iNaturalist 2019)。所有型号都进行了微调，图像分辨率为384×384。
    • 本文通过保留所有数据扩充策略，采用与预训练阶段相同的训练设置。为了在不同的分辨率下进行微调，本文还插入了新面片的位置嵌入。对于CIFAR-10和CIFAR-100，本文针对64个时期对模型进行微调，对于细粒度数据集，本文还针对300个epoch对模型进行微调。
    • 下表比较了TNT与ViT、DeiT和其他卷积网络的迁移学习结果。本文发现在大多数参数较少的数据集上，TNT的性能优于DeiT，这显示了建模像素级关系以获得更好的特征表示的优越性。
    • 
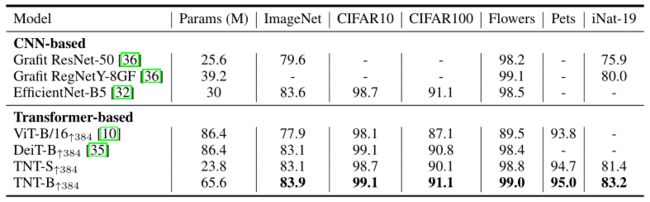
      • ImageNet预训练的下游图像分类任务的结果。↑ 384表示384×384分辨率的微调。

  • Pure Transformer Object Detection.

    • 本文通过结合TNT和DETR构建了一个纯transformer对象检测流水线。为了公平比较，本文采用PVT的训练和测试设置，并增加一个2×2的平均池，使TNT骨干网的输出规模与PVT和ResNet相同。
    • 所有比较的模型都使用AdamW进行训练，批次大小为16，50个epoch。训练图像被随机调整大小以具有在[640，800]范围内的短边和在1333像素内的长边。为了测试，短边设置为800像素。COCO val2017的结果如下表所示。在相同的设置下，具有TNT-S主干的DETR比具有代表性的纯变压器检测器DETR+PVT-小3.5 AP，具有相似的参数。
    • 
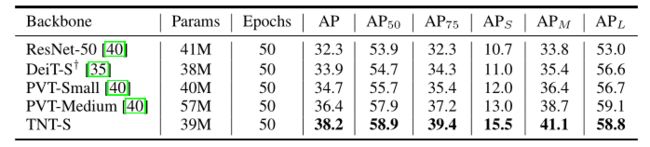
    • 在带有ImageNet预训练的COCO2017 val集上的对象检测结果。“+”表示本文实施的结果。

  • Pure Transformer Semantic Segmentation.

    • 本文采用Trans2Seg 的切分框架来构建基于TNT主干的纯变压器语义切分。为了公平比较，本文遵循PVT的训练和测试配置。所有比较的模型都由AdamW优化器训练，初始学习率为1e-4，多项式衰减时间表。在训练过程中，本文应用了512×512的随机调整大小和裁剪。
    • 单量程测试的ADE20K结果如下表所示。在参数相近的情况下，TNT-S主链的Trans2Seg达到43.6% mIoU，比PVT-small主链高1.0%，比DeiT-S主链高2.8%。
    • 
    • 使用ImageNet预训练在ADE20K val集上进行语义分割的结果。“+”表示本文实施的结果。

Conclusion

• 本文提出了一种用于视觉识别的新型transformer中transformer(TNT)网络结构。特别地，本文将图像均匀地分割成一系列小块(视觉句子)，并将每个小块视为一系列子小块(视觉单词)。本文引入了一个TNT模块，其中外部transformer模块用于处理句子嵌入，内部transformer模块用于建模单词嵌入之间的关系。
• 在线性层的投影之后，视觉单词嵌入的信息被添加到视觉句子嵌入中。本文通过堆叠TNT模块来构建TNT架构。与破坏patch局部结构的传统视觉转换器(ViT)相比，本文的TNT可以更好地保存和模拟视觉识别的局部信息。在ImageNet和下游任务上的大量实验证明了所提出的TNT体系结构的有效性。

Appendix

• Visualization of Attention Maps
  • Attention between Patches：在下图中，本文绘制了从每个补丁到所有补丁的注意力图。
    • 
    • 外部transformer块中所有贴片之间的注意力图的可视化。
  • 通过上图可以看到，对于DeiT-S和TNT-S，随着层的深入，更多的补丁是相关的。这是因为补丁之间的信息已经在更深的层次上互相充分沟通了。至于DeiT和TNT的区别，TNT的注意力可以集中在Block-12中有意义的斑块上，而DeiT仍然关注与熊猫无关的树。
  • Attention between Class Token and Patches：在下图中，本文为一些随机采样的图像绘制了类标记到所有补丁之间的注意力图。通过绘制出的图像可以看到，输出特征主要集中在与待识别对象相关的补丁上。
    • 
    • 注意力从输出标记映射到输入空间的例子。
• Exploring SE module in TNT
  • 受CNN的压缩和激发(SE)网络的启发，本文提出探索变压器的通道式注意。本文首先平均所有的句子(单词)嵌入，并使用两层MLP来计算注意力值。对所有嵌入的关注成倍增加。SE模块仅引入几个额外的参数，但是能够执行维度方式的关注以增强特征。从下表的结果来看，在TNT中加入SE模块可以进一步略微提高精度。
    • 
    • TNT中SE模块的探索。
• Object Detection with Faster RCNN
  • 作为一个通用骨干网络，TNT也可以应用于多尺度视觉模型，如faster RCNN 。本文从TNT的不同层提取特征来构造多尺度特征。特别地，FPN采用4级特征(1/4，1/8，1/16，1/32)作为输入，而每个TNT块的特征分辨率为1/16。本文从浅到深(3、6、9、12)选择4层，形成多层次的表示。
  • 为了匹配特征形状，本文以适当的步距插入反卷积/卷积层。本文用FPN 在faster RCNN上评估TNT-S和DeiT-S。DeiT模型也以同样的方式使用。COCO2017 val结果如下表所示。TNT取得比ResNet和DeiT主干网更好的性能，表明了它对类FPN框架的推广。
  • 
  • 使用ImageNet预训练在COCO minival集上进行快速RCNN对象检测的结果。"+"表示本文实施的结果。

自注意力机制

• 自注意力机制（self-Attention Mechanism），它最早由谷歌团队在2017年提出，并应用于Transformer语言模型。自注意力机制可以在编码或解码中单独使用，相对于注意力机制，它更关注输入内部的联系，区别就是Q,K和V来自同一个数据源，也就是说Q,K和V由同一个矩阵通过不同的线性变换而来。(详解自注意力机制及其在LSTM中的应用_NLP饶了我的博客-CSDN博客_自注意力机制lstm)

• 比如对于文本矩阵来说，利用自注意力机制可以实现文本内各词“互相注意”，即词与词之间产生注意力权重矩阵，然后对Value加权求和产生一个融合了自注意力的新文本矩阵。文本自注意力的实现步骤如下：

  1. 假设文本矩阵$input={\mathbb{R}}^{(a\times b)}$ ，三个变换矩阵（卷积核）：$ ω^q,ωk∈ \R^{{(b×d)}、ω}v∈ \R^{(b×c)}$ ；

  2. Q、K、V变换：文本矩阵和三个权重矩阵做线性变换，得到$Q,K\in {\mathbb{R}}^{(a\times d)}、V\in {\mathbb{R}}^{(a\times c)}$ :$Q=input\cdot {\omega }^q,K=input\cdot {\omega }^k,V=input\cdot {\omega }^v$;

  3. 缩放点积：$Q\times K^T$然后乘以一个 $1/\sqrt{d_k}$(dk为K的维度，$1/\sqrt{d_k}$为缩放因子，防止内积数值过大影响神经网络的学习），得到注意力得分矩阵$ G∈ \R^{{(a×a)}$，G的行表示某个词在各个词上的得分：$G=QK}T/\sqrt{d_k}$；

  4. 得到注意力权重矩阵：softmax(G)表示注意力权重矩阵W ：$W=softmax(\frac{Q{K}^T}{\sqrt{d_k}})$；

  5. 得到结果矩阵： W* V 得到一个结果矩阵$Attention\in {\mathbb{R}}^{(a\times c)}$，该矩阵就是一个全新的融合了注意力机制的文本矩阵z:

     • $$z=Attention(Q,K,V)=softmax(\frac{Q{K}^T}{\sqrt{d_k}})V$$

• 在上述公式中，变换矩阵${\omega }^q、{\omega }^k、{\omega }^v$都是神经网络的参数，可以随着反向传播而修改，通过修改这些变换矩阵来达到自注意力转移的目的。

多头自注意力

• 若为多头自注意力机制，则有多组卷积核$ ω_i^q,ω_iv,ω_i^k$，将步骤2-5进行h次得到h组结果矩阵 $(z_1,...,z_h)$，将$(z_1,...,z_h)$拼接并做一次线性变换${\omega }^z$ 就得到了想要的文本矩阵：$MultiHead(Q,K,V)=Concat(z_1,...,z_h){\omega }^z$.

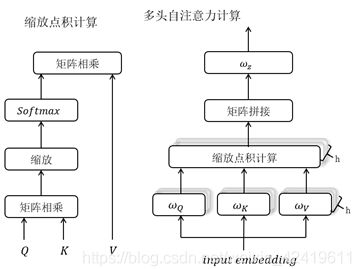
• 缩放点积计算和多头自注意力机制计算过程如下图：

  • 

  • 自注意力机制将文本输入视为一个矩阵，没有考虑文本序列信息，例如将K、V按行打乱，那么计算之后的结果是一样的，但是文本的序列是包含大量信息的.Positional Encoding计算公式如下：

    • $$\{\begin{array}{l}\begin{array}{r}PE(pos,2i)=sin(pos/10000^{2i/d_{model}})\\ PE(pos,2i+1)=cos(pos/10000^{2i/d_{model}})\end{array}\end{array}$$

    • pos 表示位置index，i表示位置嵌入index。得到位置编码后将原来的word embedding和Positional Encoding拼接形成最终的embedding作为多头自注意力计算的输入input embedding。

  • word embedding

    • Embedding在数学上表示一个maping, f: X -> Y， 也就是一个function，其中该函数是injective（就是所说的单射函数，每个Y只有唯一的X对应，反之亦然）和structure-preserving (结构保存，比如在X所属的空间上X1 < X2,那么映射后在Y所属空间上同理 Y1 < Y2)。那么对于word embedding，就是将单词word映射到另外一个空间，其中这个映射具有injective和structure-preserving的特点。

    • word embedding：NLP语言模型中对单词处理的一种方式，这种技术会把单词或者短语映射到一个n维的数值化向量，核心就是一种映射关系，主要分为两种方式：

      • one hot encoding：对语料库中的每个单词都用一个n维的one hot向量表示，其中n为语料库中不同单词的个数。这种方法的原理是把语料库中的不同单词排成一列，对于单词A，它在语料库中的位置为k，则它的向量表示为第k位为1，其余为0的n维向量。
      • 
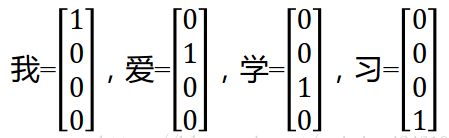
      • word2vec：可以理解为一种对单词onehot向量的一种降维处理，通过一种映射关系将一个n维的onehot向量转化为一个m维的空间实数向量（可以理解为原来坐标轴上的点被压缩嵌入到一个更加紧凑的空间内），由于onehot向量在矩阵乘法的特殊性，我们得到的表示映射关系的n*m的矩阵中的每k行，其实就表示语料库中的第k个单词。
      • 采用这种空间压缩降维的处理方式对语料库中的词进行训练，主要有两种方式
        • skip-gram神经网络训练模型：一种隐层为1的全连接神经网络，且隐层没有激活函数，输出层采用softmax分类器输出概率。输入为一个单词，输出为每个单词是输入单词的上下文的概率，真实值为输入单词的上下文中的某个单词。
        • 主要通过skip-window控制，它代表着我们从当前input word的一侧（左边或右边）选取词的数量。假如有一个句子“The dog barked at the mailman”，选取“dog”作为input word，那么最终获得窗口中的词（包括input word在内）就是[‘The’, ‘dog’，‘barked’, ‘at’]。另一个参数叫num_skips，它代表着我们从整个窗口中选取多少个不同的词作为我们的output word，当skip_window=2，num_skips=2时，将会得到两组 (input word, output word) 形式的训练数据，即 (‘dog’, ‘barked’)，(‘dog’, ‘the’)。
        • CBOW：原理与skip-gram类似，但是输入为上下文信息，输出为信息中的中心词。
        • word2vec的优点：表示单词的向量维度缩减很大，有益于后续RNN训练的收敛性。如果某两个单词的上下文很相似，则计算出来的表示这两个单词的特征向量会很相似，在空间中表示相近的物理位置，所以可以用两个单词生成的向量的长度表示其含义的远近。除了词向量的大小之外，词向量的方向还表示一种含义，若某两个词向量的方向相同，则其表示的含义也相近。

  • Positional Encoding

    • Positional Encoding(位置编码)。传统做NLP邻域使用的模型大多是RNN模型(比如说LSTM、Bi-LSTM)，基于RNN模型的训练是一个迭代的过程，也就是把一句话中的每一个词按顺序输入模型中，当RNN处理完当前的这个词时才可以输入下一个词，这种方式虽然可以使RNN按顺序读取语义信息，但是由于是串行计算，当语句较长的时候计算效率较低。
    • 谷歌大脑在2017年发布的论文《Attention is all you need》中提出了一种新型的NLP处理模型——Transfomer。Transfomer的效果非常好并且可以对语句进行并行计算，也就是同时把一句话中的所有词都输入进去同时计算，大大加快了计算效率。但是问题来了，并行计算好是好，但是怎么让模型知道一句话中每个字的顺序信息呢？这就要引出我们的Positional Encoding(位置编码)了。
    • 对CNN，只能考虑到固定前后的局部信息，RNN能考虑稍微长期的信息，LSTM是有重点的记录，Transformer只能考虑到全局的信息，尤其在bert中，只用了transformer encoder，模型上就完全丧失对位置信息的描述了，因此引入基于位置的特征就可能在特定任务中产生收益。
    • 看个例子：I believe I can be the best.
      • 对于self attention，如果没有positional encoding，两个i的输出将会一样，但是我们知道，这两个i是存在区别的，不是在指代上，而是含义上，第一个i是观点的发出者，第二个i是观点的对象，“认为我会是最棒的，不是别人”，所以从语义上两者就有所区别了，权重向量完全一样可就有问题了吧。这也是缺少位置信息的缺憾。
    • position embedding怎么做
      • 首先，最简单的模式就是对词向量矩阵直接加一层全连接层，就是全连接层。就真的是这么简单！
      • 
      • 对于每个位置的词向量，都稳定的乘以一个稳定的向量，就如上面所示，第1个位置一定对应positonal embedding的第一个向量，那这组向量抽出来。

AdamW优化算法

• 说到优化器，我们脑海中首先浮现的可能就是 Stochastic Gradient Descent （SGD）、Adaptive Gradient (AdaGrad)、Root Mean Square prop (RMSprop)、Adaptive Moment estimation (Adam) 等常用的老牌优化器。但是神经网络发展到了现在，大部分 NLP 预训练模型已不再使用这些方法，而是使用 Adam Weight Decay Regularization (AdamW) 和19年首度亮相的 Layer-wise Adaptive Moments optimizer for Batching training (LAMB)。

• 为解决 GD 中固定学习率带来的不同参数间收敛速度不一致的弊端，AdaGrad 和 RMSprop 诞生出来，为每个参数赋予独立的学习率。计算梯度后，梯度较大的参数获得的学习率较低，反之亦然。此外，为避免每次梯度更新时都独立计算梯度，导致梯度方向持续变化，Momentum 将上一轮梯度值加入到当前梯度的计算中，通过某种权重对两者加权求和，获得当前批次参数更新的更新值。 Adam 结合了这两项考虑，既为每一个浮点参数自适应性地设置学习率，又将过去的梯度历史纳入考量

• 最优化方法一直是机器学习中非常重要的部分，也是学习过程的核心算法。而 Adam 自 14 年提出以来就受到广泛关注。不过自去年以来，很多研究者发现 Adam 优化算法的收敛性得不到保证，ICLR 2017 的最佳论文也重点关注它的收敛性。大多数深度学习库的 Adam 实现都有一些问题，并在 fastai 库中实现了一种新型 AdamW 算法。

• Adam 优化器之旅可以说是过山车（roller-coaster）式的。本质上是一个出于直觉的简单想法：既然明确地知道某些参数需要移动得更快、更远，那么为什么每个参数还要遵循相同的学习率？因为最近梯度的平方告诉我们每一个权重可以得到多少信号，所以我们可以除以这个，以确保即使是最迟钝的权重也有机会发光。Adam 接受了这个想法，在过程中加入了标准方法，就这样产生了 Adam 优化器（稍加调整以避免早期批次出现偏差）！

• 随机梯度下降保持单一的学习率（即 alpha）更新所有的权重，学习率在训练过程中并不会改变；Adam 通过计算梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应性学习率。

• Adam 算法是AdaGrad和RMSProp两种随机梯度下降扩展式的优点集合;适应性梯度算法（AdaGrad）为每一个参数保留一个学习率以提升在稀疏梯度（即自然语言和计算机视觉问题）上的性能。均方根传播（RMSProp）基于权重梯度最近量级的均值为每一个参数适应性地保留学习率。这意味着算法在非稳态和在线问题上有很有优秀的性能。

• Adam 不仅如 RMSProp 算法那样基于一阶矩均值计算适应性参数学习率，它同时还充分利用了梯度的二阶矩均值（即有偏方差/uncentered variance）。具体来说，算法计算了梯度的指数移动均值（exponential moving average），超参数 beta1 和 beta2 控制了这些移动均值的衰减率。

  • α：称为学习率或步长因子，它控制了权重的更新比率（如 0.001）。较大的值（如 0.3）在学习率更新前会有更快的初始学习，而较小的值（如 1.0E-5）会令训练收敛到更好的性能。
  • β1：一阶矩估计的指数衰减率（如 0.9）。
  • β2：二阶矩估计的指数衰减率（如 0.999）。该超参数在稀疏梯度（如在 NLP 或计算机视觉任务中）中应该设置为接近 1 的数。
  • $\epsilon$：该参数是非常小的数，其为了防止在实现中除以零（如 10E-8）。

• 什么是梯度优化算法（GD梯度下降）

  • 首先定义：待优化参数：w，目标函数：f(w) ，初始学习率 α。
  • 然后，开始进行迭代优化。在每个epoch t中 ：
    • 计算目标函数关于当前参数的梯度：$g_t=▽f(w_t)$；
    • 根据历史梯度计算一阶动量和二阶动量：$m_t=\varphi (g_1,g_2,...,g_t);V_t=\psi (g_1,g_2,...,g_t)$；
    • 计算当前时刻的下降梯度：${\eta }_t=\alpha \cdot m_t/\sqrt{V_t}$；
    • 根据下降梯度进行更新：$w_{t+1}=w_t-{\eta }_t$。

• SGD-M 在SGD 基础上增加了一阶动量，AdaGrad 和 AdaDelta 在 SGD 基础上增加了二阶动量。把一阶动量和二阶动量都用起来，就是 Adam 了——Adaptive + Momentum。

  • SGD 的一阶动量：$m_t={\beta }_1\cdot m_{t-1}+(1-{\beta }_1)\cdot g_t$；
  • 加上 AdaDelta 的二阶动量：$V_t={\beta }_2\ast V_{t-1}+(1-{\beta }_2)\cdot g_t^2$；
  • $\widehat{m_t}=\frac{m_t}{1-{\beta }_1^t},\widehat{V_t}=\frac{V_t}{1-{\beta }_2^t}$。优化算法里最常见的两个超参数β1，β2 就都在这里了，前者控制一阶动量，后者控制二阶动量。

• AdamW就是Adam优化器加上L2正则，来限制参数值不可太大，这一点属于机器学习入门知识了。以往的L2正则是直接加在损失函数上，比如这样子：加入正则，损失函数就会变成这样子：

  • $$L_{l2}(\theta )=L(\theta )+\frac{1}{2}\gamma ||\theta |{|}^2$$

Drop Path

• Drop Path是NAS中常用到的一种正则化方法，由于网络训练的过程中常常是动态的，Drop Path就成了一个不错的正则化工具，在FractalNet、NASNet等都有广泛使用。Drop Path就是随机将深度学习网络中的多分支结构随机删除。