深度学习第5周：运动鞋品牌识别

第5周：运动鞋品牌识别

选题：运动鞋品牌识别
难度：新手入门
语言：Python3、TensorFlow2
时间：8月22-8月26日

要求：

跑通程序
理解卷积的运算过程
验证集准确率达到82%
参考文章：https://www.heywhale.com/mw/project/62feef0af31025b77757087a
作者：K同学啊
本文为360天深度学习训练营中的学习记录博客

一、前期工作

import pandas as pd 
import PIL
import tensorflow as tf
from tensorflow.keras import models,layers
import matplotlib.pyplot as plt
import pathlib

data_dir = 'D:\AIoT学习\深度学习训练营\第五周'
data_dir = pathlib.Path(data_dir)
data_dir

WindowsPath(‘D:/AIoT学习/深度学习训练营/第五周’)

1、查看数据

image_count = len(list(data_dir.glob('train/*/*.jpg')))
print('图片总数',image_count)
PIL.Image.open(list(data_dir.glob('*/*/*.jpg'))[0])

图片总数 502

二、数据预处理

1、加载数据

img_height = 224
img_width = 224
batch_size = 16 #考虑样本较少，batch_size设定较小
train_ds = tf.keras.preprocessing.image_dataset_from_directory(
            'D:/AIoT学习/深度学习训练营/第五周/train/',  #注意斜杠方向/
            image_size=(img_height,img_width),
            seed = 123,
            batch_size=batch_size) #502 files
val_ds = tf.keras.preprocessing.image_dataset_from_directory(
            'D:/AIoT学习/深度学习训练营/第五周/test/',
            image_size=(img_height,img_width),
            seed=123,
            batch_size=batch_size) #76files
class_names = train_ds.class_names
class_names

[‘adidas’, ‘nike’]

2、数据可视化

plt.figure(figsize=(20,10))
for image,labels in train_ds.take(1):
    for i in range(16):
        plt.subplot(5,8,i+1)
        plt.imshow(image[i].numpy().astype('uint8'))
        plt.title(class_names[labels[i]])
        plt.axis('off')
        

3、再次检查数据

for image_batch,labels_batch in train_ds:
    print(image_batch.shape) #每批图片的shape
    print(labels_batch.shape) #对应label的shape
    break

(16, 224, 224, 3)
(16,)

4、配置数据

AUTOTUNE = tf.data.AUTOTUNE
train_ds = train_ds.cache().shuffle(800).prefetch(buffer_size=AUTOTUNE)  #prefetch预读,buffer_size可以被加入缓冲器的最大元素数
val_ds = val_ds.cache().prefetch(buffer_size=AUTOTUNE)

三、构建CNN网络

num_class = 2
model = models.Sequential([
            layers.experimental.preprocessing.Rescaling(1./255,input_shape=(img_height,img_width,3)),
            layers.Conv2D(16,(3,3),activation='relu',input_shape=(img_height,img_width,3)),
            layers.BatchNormalization(),
            layers.MaxPool2D((2,2)),
            layers.Conv2D(32,(3,3),activation='relu'),
            layers.BatchNormalization(),
            layers.AveragePooling2D((2,2)),
            layers.Conv2D(64,(3,3),activation='relu'),
            layers.BatchNormalization(),
          
            
            layers.Flatten(),
            layers.Dense(128,activation='relu'),
            layers.Dropout(0.3),
            layers.Dense(2,activation='sigmoid')
])
model.summary()

这次构建神经网络，在卷积层之后添加了BN层，一方面可以提高模型泛化能力防止过拟合，另一方面可以选择较大的学习率使模型更快收敛

四、编译

对于神经网络模型而言，根据不同的输出任务而言，可以分成模式分类和模式回归两大问题。在训练神经网络时，往往采用基于梯度下降的方法不断去缩小预测值和真实值之间的差值，而这个差值就叫做损失（Loss）,计算该损失的函数就叫做损失函数（Loss function）。对于不同输出类型的神经网络模型，其损失函数是不同的，损失函数和输出层的激励函数是相互配套使用的
————————————————
版权声明：本文为CSDN博主「chengjinpei」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/chengjinpei/article/details/115858270

（1）回归任务
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IQkVajlG-1664520561898)(attachment:bab77eb4-63c0-429a-954e-479c55b19422.png)]

• 输出层神经元个数：1个
  损失函数：
  MSE(均方误差)
  输出层配套的激活函数：
  linear、sigmoid、tanh等均可以
  （2）分类任务
  二分类：
  输出神经元个数2
  损失函数：binary_crossentropy 二分类交叉熵损失函数

多分类：几个种类对应几个输出神经元
损失函数可选择categorical_crossentropy(多分类交叉熵损失函数)
sparse_categorical_crossentropy(稀疏多分类交叉熵损失函数)
配套激活函数：softmax
不同的是后者这要求target是数字编码，如：2，0，1
前者要求独热编码如[0，0，1]

新知识点：设置动态学习率

# 设置初始学习率
initial_learning_rate = 0.001

lr_schedule = tf.keras.optimizers.schedules.ExponentialDecay(#Exponential:指数的
        initial_learning_rate,
        decay_steps=10,# 敲黑板！！！这里是指 steps，不是指epochs
        decay_rate=0.92, #lr经过一次衰减会变为decay_rate*lr
        staircase=True)#如果 staircase=True，那就表明每decay_steps次计算学习速率变化，更新原始学习速率，如果是False，那就是每一步都更新学习速率

学习率大与学习率小的优缺点分析:

学习率大

● 优点：
○ 1、加快学习速率。
○ 2、有助于跳出局部最优值。
● 缺点：
○ 1、导致模型训练不收敛。
○ 2、单单使用大学习率容易导致模型不精确。

学习率小

● 优点：
○ 1、有助于模型收敛、模型细化。
○ 2、提高模型精度。
● 缺点：
○ 1、很难跳出局部最优值。
○ 2、收敛缓慢。
注意：这里设置的动态学习率为：指数衰减型（ExponentialDecay）。在每一个epoch开始前，学习率（learning_rate）都将会重置为初始学习率（initial_learning_rate），然后再重新开始衰减。

opt = tf.keras.optimizers.Adam(learning_rate=lr_schedule) #

model.compile(optimizer=opt,
             loss=tf.keras.losses.SparseCategoricalCrossentropy(),#Use this crossentropy loss function when there are two or more labelclasses.
             metrics=['accuracy'])

知识点2.早停与保存最佳模型参数

EarlyStopping()参数说明：

• monitor: 被监测的数据。
• min_delta: 在被监测的数据中被认为是提升的最小变化， 例如，小于 min_delta 的绝对变化会被认为没有提升。
• patience: 没有进步的训练轮数，在这之后训练就会被停止。
• verbose: 详细信息模式。
• mode: {auto, min, max} 其中之一。 在 min 模式中， 当被监测的数据停止下降，训练就会停止；在 max 模式中，当被监测的数据停止上升，训练就会停止；在 auto 模式中，方向会自动从被监测的数据的名字中判断出来。
• baseline: 要监控的数量的基准值。 如果模型没有显示基准的改善，训练将停止。
• estore_best_weights: 是否从具有监测数量的最佳值的时期恢复模型权重。 如果为 False，则使用在训练的最后一步获得的模型权重。

from tensorflow.keras.callbacks import ModelCheckpoint,EarlyStopping

epochs = 50

#保存最佳模型
checkpoint = ModelCheckpoint(filepath = 'best_modelweek5.h5',
                            monitor = 'val_accuracy',
                            verbose = 1,
                            save_best_only = True,
                            save_weights_only =True)
#设置早停
earlystopper = EarlyStopping(monitor='val_accuracy',min_delta=0.001,patience=10,verbose=1)

history = model.fit(train_ds,
                   validation_data=val_ds,
                    epochs=epochs,
                    callbacks=[checkpoint,earlystopper])

Epoch 1/50
32/32 - loss: 37.9714 - accuracy: 0.5677
Epoch 1: val_accuracy improved from -inf to 0.51316, saving model to best_modelweek5.h5
32/32 - loss: 37.9714 - accuracy: 0.5677 - val_loss: 2.3826 - val_accuracy: 0.5132
Epoch 2/50
32/32 - loss: 8.5753 - accuracy: 0.7032
Epoch 2: val_accuracy did not improve from 0.51316
…
Epoch 31: val_accuracy did not improve from 0.89474
32/32 - loss: 0.0687 - accuracy: 0.9761 - val_loss: 2.7008 - val_accuracy: 0.8816
Epoch 31: early stopping

五、模型评估

1. Loss与Accuracy图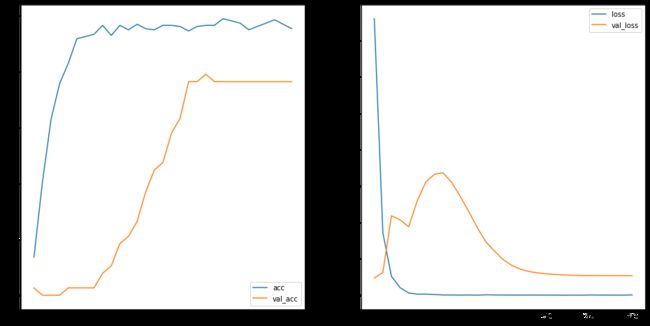

2、图片预测

import numpy as np
model.load_weights('best_modelweek5.h5')
img = PIL.Image.open(r'D:\AIoT学习\深度学习训练营\第五周\test\adidas\36.jpg') 
image = np.array(img)
image = tf.image.resize(image,size=(224,224))

img_array = tf.expand_dims(image,0)
predictions = model.predict(img_array)
print('预测结果为：',class_names[np.argmax(predictions)])

1/1 [==============================] - 0s 40ms/step
预测结果为： adidas

总结

1、交叉熵

图片来源https://blog.csdn.net/superjunenaruto/article/details/108358905
因此对于二分类问题
$$L=-\frac{1}{N}\sum _{n=1}^{\mathbb{N}}{y}^{(n)}log{y}^{\prime (n)}+(1-y^{(n)})log(1-y^{\prime (n)})$$
对于多分类问题
$$L=-\frac{1}{N}\sum _{n=1}^{\mathbb{N}}\sum _{c=1}^C{y}_c^{(n)}log{y}_c^{\prime (n)})$$
其中c为类别数据。可见，当二分类数据输出神经元为2个以独热编码形式输出时，二分类问题交叉熵可以用多分类交叉熵损失函数表示
2、对于不同的问题应该采用不同的损失函数方案，回归问题多采用MSE，分类问题则多使用交叉熵损失函数。
3、categorical_crossentropy(多分类交叉熵损失函数)
sparse_categorical_crossentropy(稀疏多分类交叉熵损失函数)的不同
后者要求target是数字编码，如：2，0，1
前者要求独热编码如[0，0，1]
在本次案例中labels通过单个数字0，1表示类别，而不是数组[1,0],[0,1]因此选择系数多分类交叉熵损失函数
4、初始学习率可以设置的较大，有助于跨越局部最优解，当多轮学习过后目标度量指标始终没有明显变化可以考虑缩小学习率，有助于模型收敛、模型细化。