【DeepDTA模型解读】

1.数据集 Datasets

(1)Davis

Comprehensive analysis of kinase inhibitor selectivity @ Nat. Biotechnol.2011
442蛋白-68配体，30056对相互作用
dissociation constant (Kd) → $p{K}_d=-1og(\frac{K_d}{1e9})$

(2)KIBA

Making sense of large-scale kinase inhibitor bioactivitydata sets: a comparative and integrative analysis @J. Chem. Inf. Model2014
467靶点-52498药物
过滤：至少10对相互作用 → 229蛋白 - 2111药物，118254对相互作用
KIBA（Ki,Kd,IC50) → 构建KIBA分数：Simboost: a read-across approach for predicting drug–target binding affinities using gradient boosting machines.@J. Cheminform.2017

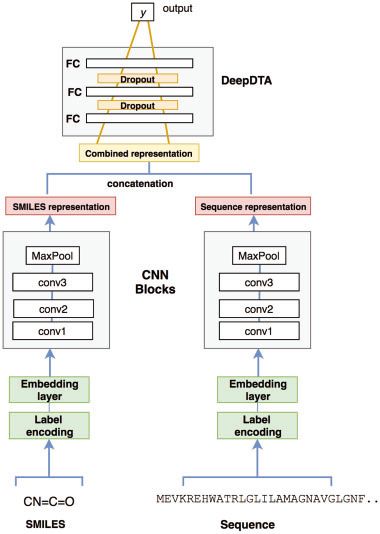
2. 输入表示

(1)SMILE

eg. [C N = C = O] = [1 3 63 1 63 5]
64 labels 固定最大长度 85 （Davis） 100 （KIBA）← 基于分布，cover 80% 蛋白，90%化合物

$>$maximum length 被截断，短序列用0填充

(2) 蛋白序列

Label encoding
25 categories 固定最大长度1200（Davis) 1000(KIBA)

3. 模型

激活函数：ReLU $g(x)=max(0,x)$
回归任务→ MSE损失函数

$$MSE=\frac{1}{n}\sum _{i=1}^n(P_i-Y_i{)}^2$$

P 是预测向量， Y是真实值向量, n 是样本数量

训练100 个周期，mini-batch size = 256

优化算法 Adam 默认学习率 0.001

使用 Keras Embedding layer ，用128维 dense向量 表示符号

Davis 输入（85，128）和（1200，128）
KIBA 输入 （100，128）和（1000，128）

Concordance Index (CI)测量模型表现，与KronRLS 和 SimBoost 比较

4.实验与结果

(1)Baselines

Kron-RLS的目的是 最小化下面函数，f 是预测函数
$$J(f)=\sum _{i=1}^m(y_i-f(x_i){)}^2+\lambda ||f|{|}_k^2$$
$||f|{|}_k^2$是 f 的范数，与 核函数k 有关； $\lambda >0$ 是正则超参数，由用户定义
$J(f)$ 的最小值可以定义为：
当$$f(x)=\sum _{i=1}^m{a}_{i}k(x,x_i)$$ 时
$k$是核函数，$J(f)$取得最小。

为了表示化合物，用相似性矩阵表示，由Pubchem structure clustering server(Pubchem Sim)@http://pubchem.ncbi.nlm.nih.gov
对于蛋白 用Smith-Waterman 算法去构建蛋白相似性矩阵

SimBoost
药物，靶点， 药物-靶点对 构建特征
这些特征 喂到 监督学习方法（梯度提升回归树）

任意药物-靶点对 $d{t}_i$, 预测的结合亲和力分数 $\overline{y_i}$ 表示为：
$$\overline{y_i}=\theta (d{t}_i)=\sum _{m=1}^M{f}_m(d{t}_i),f_m\in F$$
M 表示回归树的数量，F表示所有可能的树的空间

正则化目标函数 去学习树$f_m$的参数：

$$R(\theta )=\sum _{i}l(y_i,\overline{y_i})+\sum _m\alpha (f_m)$$

$l$是损失函数：测量实际亲和力$y_i$与预测值$\overline{y_i}$的差异，
$\alpha$是控制模型复杂度的调整参数
为了表示化合物，用相似性矩阵表示，由Pubchem structure clustering server(Pubchem Sim)@http://pubchem.ncbi.nlm.nih.gov
对于蛋白 用Smith-Waterman 算法去构建蛋白相似性矩阵

(2)评价方法

Concordance Index (CI)

$$CI=\frac{1}{Z}\sum _{{\delta }_i>{\delta }_j}h(b_i-b_j)$$

where $b_i$ is the prediction value for the larger affinity ${\delta }_i$, $b_j$ is the prediction value for the smaller affinity ${\delta }_j$, $Z$ is a normalization constant,
$h(x)$ 是阶梯函数
$$h(x)=\{\begin{array}{l}1\text{if x>0}\\ 0.5\text{if x=0}\\ 0\text{if x<0}\end{array}$$

MSE

(3)实验设置

数据平分6份，5-fold 交叉验证
确定3 个超参数：过滤器数量（蛋白与化合物相同）
化合物的过滤器尺寸长度，蛋白过滤器尺寸的长度

在验证集上最好的平均CI分数的超参数组合被选为最好的组合去model the test set.

先大范围选，在微调超参数，eg.确定过滤器数量：搜索[16,32，64，128，512], 如果 16最好，范围更新为[4,8,16,20]

使用 $r_m^2$ 和$AUPR$评价所获模型在测试集上的表现

参考文献：Bioinformatics, 34, 2018, i821–i829
doi: 10.1093/bioinformatics/bty593