图注意力网络(GAT)理论推导的整理
图注意力网络(GAT)理论推导的整理
- GAT的提出
-
- GAT的提出背景
- 注意力机制的引入
- GAT的结构
-
- 图注意力层
- 计算注意力系数
- 多头图注意力层
- 相关比较
- 总结
tips:本篇博客是本人因学习而整理,为方便归档而发布。博客除参考《Graph Attention Networks》(Yoshua Bengio et. al. 2017)外,也参考了网上各路大神的文章,若有侵犯或错误请私信,本人会第一时间作出回应。
GAT的提出
GAT的提出背景
图卷积网络(GCN)存在一定缺陷。GCN只能应用于转导(transductive)任务,无法完成动态图处理(inductive)。且由于傅立叶变换推导的局限性,难以处理有向图。因此,需要一种更完善的图卷积算法。
注意力机制的引入
Yoshua Bengio团队在CNN的基础上引入masked self-attention,提出了图注意力网络(GAT)1,图中的每个节点可以根据邻居节点的特征,为其分配不同的权值,并且无需使用预先构建好的图。
GAT的结构
图注意力层
首先来介绍单个的图注意力网络层。
图注意力层的结构如下图所示:
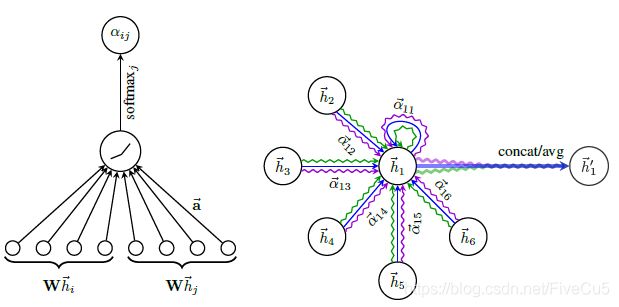
我们将输入的特征向量 h = { h 1 → , h 2 → , … h N → } , h i → ∈ R F h=\{ \overrightarrow{h_1},\overrightarrow{h_2},\ldots\overrightarrow{h_N} \},\overrightarrow{h_i}\in R^F h={h1,h2,…hN},hi∈RF经过一个以注意力为核心的聚合操作,输出一个新的特征向量。 h = { h 1 ′ → , h 2 ′ → , … h N ′ → } , h i ′ → ∈ R F ′ h=\{ \overrightarrow{h_{1}'},\overrightarrow{h_{2}'},\ldots\overrightarrow{h_{N}'} \},\overrightarrow{h_{i}'}\in R^{F'} h={h1′,h2′,…hN′},hi′∈RF′来强化feture。
我们将这个聚合操作称为图注意力层(Graph Attention Layer)。
下面来介绍具体操作。
计算注意力系数
为了获得更高级的表达能力,需要把输入的特征转换为更高维的特征(higher-level feture)。我们先初始化一个矩阵 W ( W ∈ R F ′ × F ) W(W\in R^{F'\times F}) W(W∈RF′×F),再定义一个映射 a : R F ′ × R F → R a:R^{F'}\times R^{F}\rightarrow R a:RF′×RF→R,通过self-attention,计算出两个节点间的权重关系:
e i j = a ( W h i → , W h j → ) (1) e_{ij}=a(W\overrightarrow{h_i},W\overrightarrow{h_j})\tag{1} eij=a(Whi,Whj)(1)
在这个公式中,我们通过W矩阵对顶点特征进行增维。然后,通过masked attention,将顶点 i , j i,j i,j变换后的特征拼接,再计算i节点的邻居节点j,这么做改善了过去模型中每个节点都会进行两两运算而忽略图结构信息的问题。最后,通过a映射,把拼接后的高维特征映射到一个实数上。
之后,为求得注意力系数,我们使用softmax进行正则化处理:
a i j = s o f t m a x j ( e i j ) = e x p ( e i j ) ∑ k ∈ N i e x p ( e i k ) (2) a_{ij}=softmax_j(e_{ij})=\frac{exp(e_{ij})}{\sum_{k\in N_i}^{}exp(e_{ik}) }\tag{2} aij=softmaxj(eij)=∑k∈Niexp(eik)exp(eij)(2)
在实验中,我们又进一步加入了LeakyReLU函数,所得完整公式如下:
a i j = e x p ( L e a k y R e L U ( a → T ∣ W h i → ∣ ∣ W h j → ∣ ) ) ∑ k ∈ N i e x p ( L e a k y R e L U ( a → T ∣ W h i → ∣ ∣ W h j → ∣ ) ) (3) a_{ij}=\frac{exp(LeakyReLU(\overrightarrow{a}^T| W\overrightarrow{h_i}|| W\overrightarrow{h_j}| ))}{\sum_{k\in N_i}^{}exp(LeakyReLU(\overrightarrow{a}^T| W\overrightarrow{h_i}|| W\overrightarrow{h_j}| ))}\tag{3} aij=∑k∈Niexp(LeakyReLU(aT∣Whi∣∣Whj∣))exp(LeakyReLU(aT∣Whi∣∣Whj∣))(3)
把所求注意力模型特征加权求和,可得:
h i ′ = σ ( ∑ j ∈ N i a i j W h → j ) (4) h_{i}'=\sigma \left(\sum_{j\in \mathcal{N}_i }a_{ij}W\overrightarrow{h}_j\right) \tag{4} hi′=σ⎝⎛j∈Ni∑aijWhj⎠⎞(4)
多头图注意力层
为了使self-attention更加稳定,我们引入了multi-head attention(transformer),对(4)式调用K组相互独立的注意力,然后将输出结果连接(concatenated)在一起:
h i ′ = ∥ k = 1 K σ ( ∑ j ∈ N i a i j k W k h → j ) (5) h_{i}'=\|_{k=1}^{K} \sigma \left(\sum_{j\in \mathcal{N}_i }a_{ij}^k W^k\overrightarrow{h}_j\right) \tag{5} hi′=∥k=1Kσ⎝⎛j∈Ni∑aijkWkhj⎠⎞(5)
其中||表示拼接操作, a i j k a_{ij}^k aijk表示第k次注意力系数, W k W^k Wk表示第k组线性变换矩阵。但是如果我们在最后一层(即prediction)中使用multi-head attention,连接(concatenated)输出的特征向量维度过多,就并不合适。所以我们使用averging来得到 h → i \overrightarrow{h}_i hi
h i ′ = σ ( 1 K ∑ k = 1 K ∑ j ∈ N i a i j k W k h → j ) (6) h_{i}'=\sigma \left(\frac{1}{K}\sum_{k=1}^{K}\sum_{j\in \mathcal{N}_i }a_{ij}^k W^k\overrightarrow{h}_j\right)\tag{6} hi′=σ⎝⎛K1k=1∑Kj∈Ni∑aijkWkhj⎠⎞(6)
相关比较
在第二章提出的图注意力层有效解决了传统图网络结构没能解决的以下问题:
- GAT效率更高。相比于其他图模型,GAT无需使用特征值分解等复杂的矩阵运算。
单层GAT的时间复杂度为 O ( ∣ V ∣ F F ′ + ∣ E ∣ F ′ ) O(|V|FF'+|E|F') O(∣V∣FF′+∣E∣F′)。
其中, |V|与 |E|分别表示图中节点的数量与边的数量。 - 相比于GCN,GAT中每个节点的相关性可以是不同的,因此,GAT具有更强的表示能力。
- 对于图中的所有边,attention机制是共享的。因此GAT也是一种局部模型。也就是说,在使用GAT时,我们无需访问整个图,而只需要访问所关注节点的邻节点即可。这一特点的作用主要有:
- 可以处理有向图(若 j → i j\rightarrow i j→i不存在,仅需忽略 a i j a_ij aij即可)。
- 可以被直接用于进行归纳学习。
- GraphSAGE通过从每个节点的邻居中抽取固定数量的节点,从而保证其计算的一致性。这意味着,在执行时,我们无法访问所有的邻居节点。然而,本文所提出的模型是建立在所有邻节点上的,而且无需假设任何节点顺序。
- GAT可以被看作是MoNet的一个特例。具体来说,可以通过将伪坐标函数(pseudo-coordinate function)
设为 u ( x , y ) = f ( x ) ∣ ∣ f ( y ) u(x,y)=f(x)||f(y) u(x,y)=f(x)∣∣f(y),其中, f ( x ) f(x) f(x)表示节点 x x x 的特征, || 表示连接符号;相应的权值函数则变成了
w j ( u ) = s o f t m a x ( M L P ( u ) ) w_j(u)=softmax(MLP(u)) wj(u)=softmax(MLP(u)) 。
总结
图注意力网络(GATs)是一种新型的卷积式神经网络,利用masked self-attention对图形结构数据进行操作。受益于注意力机制,GAT能够过滤噪音邻居,提升模型表现并可以对结果实现一定的解释。
图形注意网络有几个潜在的改进和扩展,可以作为未来的工作来处,以便能够处理更大的批处理大小。一个特别有趣的研究方向是利用注意机制对模型的可解释性进行深入分析。此外,从应用的角度来看,将该方法扩展到执行图分类而不是节点分类也是有意义的。最后,将模型扩展到包含边缘特性(可能表示节点之间的关系),这将允许我们处理更多的问题。
《Graph Attention Networks》(Yoshua Bengio et. al. 2017) ↩︎