机器学习：何为PR曲线与ROC曲线

PR曲线实则是以precision（精准率）和recall（召回率）这两个为变量而做出的曲线，其中recall为横坐标，precision为纵坐标。

想要明白何为precision（精准率）和recall（召回率）首先要明白混淆矩阵的概念。混淆矩阵有四个分类，如图所示。

• TP（True Positive）：指正确分类的正样本数，即预测为正样本，实际也是正样本。
• FP（False Positive）：指被错误的标记为正样本的负样本数，即实际为负样本而被预测为正样本，所以是False。
• TN（True Negative）：指正确分类的负样本数，即预测为负样本，实际也是负样本。
• FN（False Negative）：指被错误的标记为负样本的正样本数，即实际为正样本而被预测为负样本，所以是False。
• TP+FP+TN+FN：样本总数。
• TP+FN：实际正样本数。
• TP+FP：预测结果为正样本的总数，包括预测正确的和错误的。
• FP+TN：实际负样本数。
• TN+FN：预测结果为负样本的总数，包括预测正确的和错误的。

一个阈值对应PR曲线上的一个点。通过选择合适的阈值，比如50%，对样本进行划分，概率大于50%的就认为是正例，小于50%的就是负例,从而计算相应的精准率和召回率。（选取不同的阈值，就得到很多点，连起来就是PR曲线）

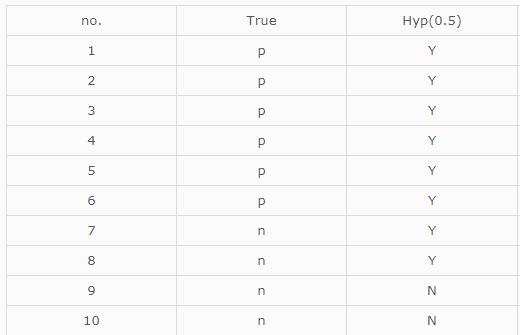
举个例子如下：(true这列表示正例或者负例，hyp这列表示阈值0.5的情况下，概率是否大于0.5)

由上图易知：TP=6，FN=0，FP=2，TN=2。因此recall=6/(6+0)=1,precison=6/(6+2)=0.75，那么得出坐标（1，0.75）。同理得到不同阈下的坐标，即可绘制出曲线。

PR曲线大致如下：

如果一个学习器的P-R曲线被另一个学习器的P-R曲线完全包住，则可断言后者的性能优于前者，例如上面的A和B优于学习器C。但是A和B的性能无法直接判断，我们可以通过平衡点判断。平衡点（BEP）是P=R时的取值，如果这个值较大，则说明学习器的性能较好。

接下来介绍ROC曲线。在ROC曲线中，横轴是假正例率（FPR），纵轴是真正例率（TPR）。

(1)真正类率(True Postive Rate)TPR: TP/(TP+FN),代表分类器预测的正类中实际正实例占所有正实例的比例。
(2)负正类率(False Postive Rate)FPR: FP/(FP+TN)，代表分类器预测的正类中实际负实例占所有负实例的比例。
我们可以发现：TPR=Recall。
ROC曲线也需要相应的阈值才可以进行绘制，原理同上的PR曲线。

举个例子如下：

如下是20个测试样本，第一列代表样本id，第二列代表他们的真实类别（p表示正样本，n表示负样本），最后一列代表训练好的模型A认为每个样本是正样本的概率。

下面就是此训练好的模型A的ROC曲线的画法：
第一步：按照属于‘正样本’的概率将所有样本排序（如上图所示）
第二步：把分类阈值设为最大，即把所有样例均预测为反例，所以此时得到P和R均为0，即(0,0)
第三步:让我们依次来看每个样本。
对于样本1，如果我们将他的score值做阈值，也就是说，只有score大于等于0.9时，我们才把样本归类到正样本，这么一来， 在ROC曲线图中，样本1对应的混淆矩阵为:
 

真实情况	预测结果
	正例	反例
正例	1	9
反例	0	10

第一个样本score=0.9，所以预测为正样本，其本身也为正样本，其他样本score都<0.9，所以都预测为负样本，从混淆矩阵中，我们可以算出X轴坐标（false positive rate）= 0/（0+10）= 0 和Y轴坐标（true positive rate）= 1/（1+9）= 0.1，所以第一个点为(0,0.1)

对于样本2，如果我们将他的score值做阈值，也就是说，只有score大于等于0.8时，我们才把样本归类到正样本，这么一来， 在ROC曲线图中，样本2对应的混淆矩阵为:

真实情况	预测结果
	正例	反例
正例	2	8
反例	0	10

第一个和第二个样本score>=0.8，所以预测为正样本，其本身也为正样本，其他样本score都<0.9，所以都预测为负样本，从混淆矩阵中，我们可以算出X轴坐标（false positive rate）= 0/（0+10）= 0 和Y轴坐标（true positive rate）= 2/（2+8）= 0.2，所以第二个点为(0,0.2)

后面都类似，依次将分类阈值设为每个样例的预测值，即依次将每个样例划分为正确。一共可以得到20个点，所画的ROC曲线如下图所示：

 样本数量越多，ROC曲线就越平滑。 

以下借鉴博客ROC曲线绘制（Python）实现简易ROC曲线的绘制。

以支持向量机模型为例。

先导入需要使用的包，使用roc_curve这个函数绘制ROC曲线。

from sklearn.svm import SVC
from sklearn.metrics import roc_curve
from sklearn.datasets import make_blobs
from sklearn. model_selection import train_test_split
import matplotlib.pyplot as plt
%matplotlib inline

然后使用下面make_blobs函数，生成一个二分类的数据不平衡数据集；

使用train_test_split函数划分训练集和测试集数据；

训练SVC模型。

X,y = make_blobs(n_samples=(4000,500), cluster_std=[7,2], random_state=0)
 
X_train,X_test,y_train, y_test = train_test_split(X,y,random_state=0)
 
clf = SVC(gamma=0.05).fit(X_train, y_train)

X,y = make_blobs(n_samples=(4000,500), cluster_std=[7,2], random_state=0)
 
X_train,X_test,y_train, y_test = train_test_split(X,y,random_state=0)
 
clf = SVC(gamma=0.05).fit(X_train, y_train)

 

从上面的代码可以看到，我们使用roc_curve函数生成三个变量，分别是fpr,tpr, thresholds，也就是假正例率（FPR）、真正例率（TPR）和阈值。

而其中的fpr,tpr正是我们绘制ROC曲线的横纵坐标，于是我们以变量fpr为横坐标，tpr为纵坐标，绘制相应的ROC图像如下：