2020李宏毅机器学习笔记
还没看完,一周内更完。。
笔记目录
- Regression (回归)
-
- Case Study (p3)
- Basic Concept (p4)
- Classification (p10)
- Logistic Regression (p11)
Regression (回归)
Case Study (p3)
机器学习的三个步骤:
- 定义模型,线性?合理性?
- 定义损失函数来判断模型的好坏
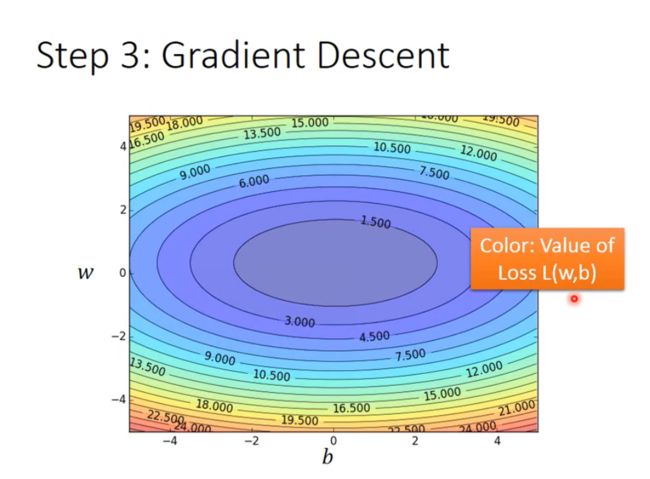
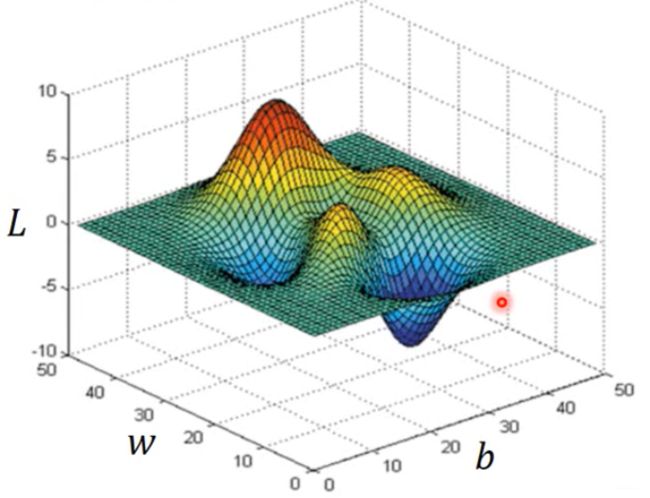
- 梯度下降法求使得loss最小的模型里面的参数
建立模型:
定义损失函数:
求使得loss最小的function,即函数里面的参数

线代貌似可以直接解step3里面的式子,但是忘记了,老师介绍的是Gradient Descen(梯度下降法)。
通过测试一次到五次的model的loss,发现过拟合了,但是想要获得更好的结果,于是back。
Overfitting(过拟合):在training有好结果,但是在testing上面的结果烂掉了。
step1:Redesign the model
数据量的不够导致过拟合的问题,采集了更多的数据之后发现,宝可梦的cp值与物种有关,即存在数据上的初始分嘞情况。
同时可以进一步考虑,是否还有别的因素可能影响?
但是一旦进一步考虑,那么函数式子又会变得很复杂,函数式子一旦变得很复杂就很有可能导致Overfitting。
step2:Regularization(正则化)
在loss function后面加一项,主要是针对w,只要w越小,那么自变量的变化就会对loss的影响就越小,即越平滑。但是前面那个参数要手调,然后找到合适大小的。
Basic Concept (p4)
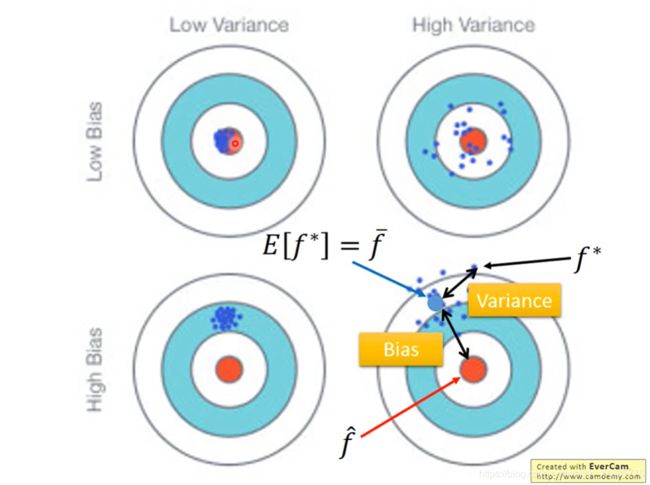
error(误差)来源于哪里?bias(偏差)还是variance(方差)?
Classification (p10)
感觉Classification和Logistic Regression这两节数学上面很美,要认真听,又一次感觉数学的奇妙。需要注意的是这两节的分类都是对于二分类问题,也就是对两个群体分类,对多个群体的分类在后续回讨论,这里挖个坑,后面很精彩。
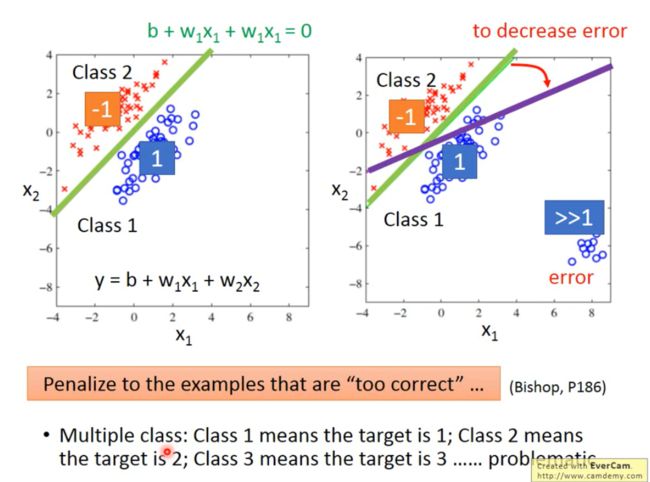
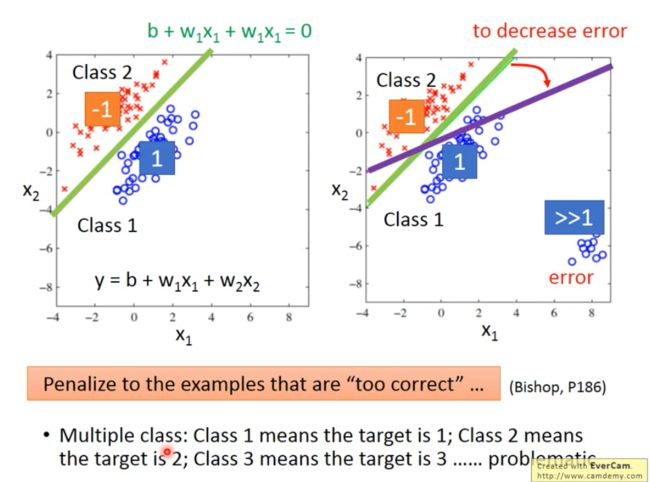
思考:因为探究的是分类,能不能把它当作是Regression进行train?也就是对于Class 1的目标设为1,Class2的目标设为-1?
那么我们会发现,本应该绿色的线才是更好的分类标准,却因为右下角远大于1的data加入使得分类准则训练成了紫色的线,这样明显是错误的,这样分类的标准就被目标本身的值所过大的影响,比如我们把所有大于0的值归为同一类,那么2和3就是一样的,但是Regression这种分类方法就会告诉你3要比2更好,更像这一种类,但实际上他们是没有什么区别的。
因此我们理想的模型和损失函数应该如下所示,这里损失函数是预测错误的次数,这里有其他的模型也可以解决这种分类问题:Perception(感知机模型)、SVM(支持向量机),这门课程是从概率的角度进行讨论,其实从不同的模型去分析讨论,最后的效果会不一样。

那么如何从概率的角度来思考这个问题呢?先观察下面的两种分类以及概率模型,那么我们就可以知道:如果给我一个宝可梦,那么我就能知道它在Class1的概率大还是Class2的概率大,哪个大哪个就是正确答案。 一定要理解这句话,太关键了,这是从概率到分类的一个思维上的转换,其实很好理解,但是我看到后面有时候老会忘记然后回头来重新看一遍。
现在我们不难发现,对于给我们一个x,我们可以通过条件概率算出它属于Class1或者Class2的概率,现在我们只需要求得条件概率 P ( x ∣ C 1 ) P(x|C_1) P(x∣C1)和 P ( x ∣ C 2 ) P(x|C_2) P(x∣C2)就可以求出分类了。
 好,那么接下来我们需要思考一个问题,就是对任意给定的x,它属于Class1的概率应该怎么算呢?比如一只给你一直原盖海龟,要计算它属于水系宝可梦的概率,由于我们在目前的水系宝可梦data里面没有见过它,那这它是水系宝可梦的概率就一定是0吗?其实不是的,这里采用Gaussian distribution来建立模型。这里需要先说明一下,宝可梦一共有7种属性,但是为了现在方便数学上面的推到我们只选择两个属性求Gaussion distribution。
好,那么接下来我们需要思考一个问题,就是对任意给定的x,它属于Class1的概率应该怎么算呢?比如一只给你一直原盖海龟,要计算它属于水系宝可梦的概率,由于我们在目前的水系宝可梦data里面没有见过它,那这它是水系宝可梦的概率就一定是0吗?其实不是的,这里采用Gaussian distribution来建立模型。这里需要先说明一下,宝可梦一共有7种属性,但是为了现在方便数学上面的推到我们只选择两个属性求Gaussion distribution。
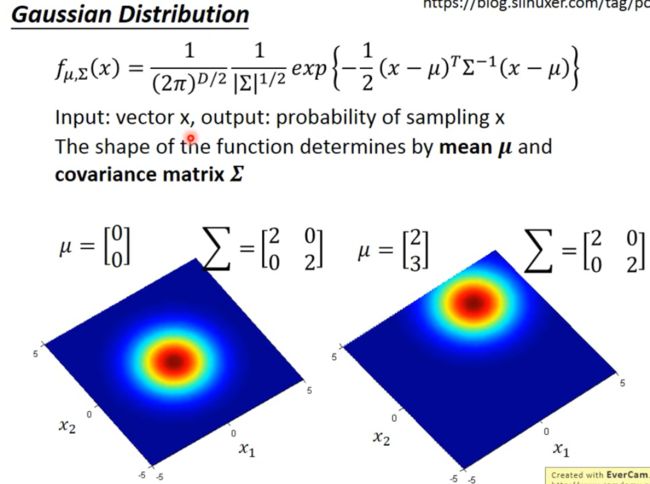
这里不对高斯分布做详细的讨论,可以自行翻阅概率论课本。需要注意的是,这里的 G a u s s i o n ( μ ∗ , Σ ∗ ) Gaussion(\mu ^{\ast},\Sigma ^{\ast}) Gaussion(μ∗,Σ∗)。这里面不是普通的均值和方差,其中 μ ∗ \mu ^{\ast} μ∗是各变量的均值,是一个多维的数组, Σ ∗ \Sigma ^{\ast} Σ∗是协方差矩阵。
于是我们的损失函数,或者说我们的优化目标,也就是要找到一个Gaussion distribution使得我们目前所有水系宝可梦它是水属性的可能性越大。


Generative model 补充: 这里我们可以对这个模型进行进一步的考虑,如果对于一只皮卡丘,我们对其用Gaussion distribution去计算它属于水属性的概率,这个概率不是为0的,这个值很小,很小的概率也不是不可能发生阿,那是不是意味着皮卡丘有可能也是水属性的呢?稍加思考我们会发现,这个模型是一个Generative model(生成模型),顾名思义,它的概率是generate出来的,就好比高中生物里面Aa*Aa,我们是考虑A和a(在机器学习里面其实可以称作特征),也就是说我们是先学习每一个水属性宝可梦的特征值,再通过我们学习到的特征值去判断testing data里面一直新的宝可梦的属性。Generative model与我们后续要学习的Logistic model是有区别的,后续会进一步介绍。 好,那我们现在就可以做分类了,给定的一个x,如果 P ( x ∣ C 1 ) P(x|C_1) P(x∣C1)>0.5那么它就属于Class1
 但非常可惜,最后的结果坏掉了,只有47%的正确率,并且就算我们考虑所有的属性一共7种,从7维的角度去算,仍然只有54%正确率。为什么?
但非常可惜,最后的结果坏掉了,只有47%的正确率,并且就算我们考虑所有的属性一共7种,从7维的角度去算,仍然只有54%正确率。为什么? 
对于下面两个属性的二维Gaussion distribution,他们的covariance matrix不同,那model的参数可能就太多了,那么最后模型的variance就大,那就容易overfitting,这还是二维情形下,如果7-dim情形下那必然overfitting,所以我们可以考虑给一个同样的协方差矩阵。其实也很容易理解为什么给相同的协方差而不是相同的均值,均值相当于打靶的靶心,而协方差是偏离值。

新的协方差矩阵简单的把之前的两个按比例相加就好。那么我们重新计算,可以得到73%的正确率,发现有比较大的提升。
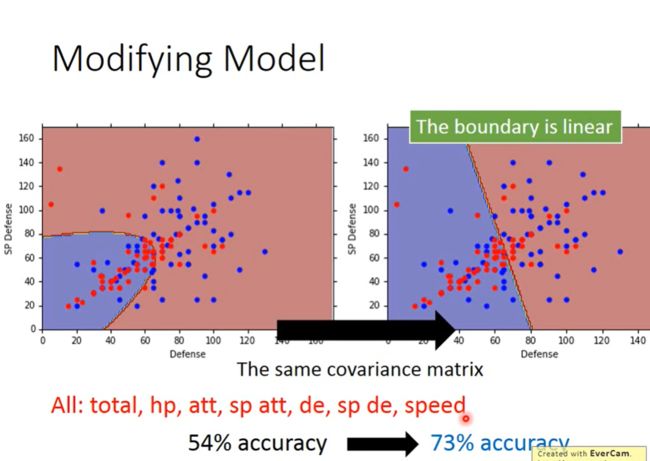
补充: 看老师说这里由于boundary是线性的,所以这种也属于linear model,我想了一下为什么这里的boundary会是直线。其实还是很容易想明白,两个协方差矩阵一样的话,也就是说两个Gaussion的概率密度从中间衰减的速度是一样的,又因为这里只有两个中心,那两个中心的发散的中线就是boundary了。
思考:为什么这里采用的是Gaussion分布而不是别的?
其实这里可以用的很多别的模型,不局限于高斯分布,如果模型简单,那么bias就大,variance就小,模型复杂bias就小,variance就大,所以我们应该根据我们具体的dataset去选择我们的模型。比如一个案例是boundary的,也就是说它的output就是yes or no,那么这种就更适合用Bernoulli distribution;如果一个案例它的各个feature是独立的,没有关联的,那他们的协方差矩阵除了对角线的地方就都是0了,就变成了7个1-D Gaussion,但我们这里的案例各个feature并不是独立的。
接下来是一部分数学推导,推导的是 P ( x ∣ C 1 ) P(x|C_1) P(x∣C1)如何变成 σ ( z ) \sigma (z) σ(z)其中 z = w ⋅ x + b z=w·x+b z=w⋅x+b。数学不好的这里可以直接记住结论,不过不建议这么做,人工智能的本质其实是数学的应用,后续会用到很多这个结论。
插播一个冷知识:Posterior Probability(后验概率),举例区分普通条件概率与后验概率的区别:
1)那么如果我们出门之前我们听到新闻说今天路上出了个交通事故,那么我们想算一下堵车的概率,这个就叫做条件概率 。也就是P(堵车|交通事故)。这是有因求果。
2)如果我们已经出了门,然后遇到了堵车,那么我们想算一下堵车时由交通事故引起的概率有多大,那这个就叫做后验概率 (其实也是条件概率,但是通常习惯这么说) 。也就是P(交通事故|堵车)。这是有果求因。
首先,我们对Posterior Probability进行分析,我们可以讲原来的式子化作一个 σ ( z ) \sigma (z) σ(z),然后我们现在进一步探讨这里的 z z z。

这部分直接贴图了。。。



这里简单的做个总结,其实就是把Gaussion分布的式子带进去计算,然后会得到一个 z z z关于 x x x的式子,仔细观察 x x x前面的系数我们会发现其实就是一个vector,然后后面那一长串其实只是一个常数。
那么,我们为什么不直接去找 w w w和 b b b 而要大费周章的去找下面那五个东西的取值再去计算 w w w和 b b b呢?
下一节介绍…
Logistic Regression (p11)
未完待续…睡觉去了
编辑于——3月29号 22:19