机器学习笔记分类与回归问题深度学习参数介绍及CNN网络搭建介绍
目录
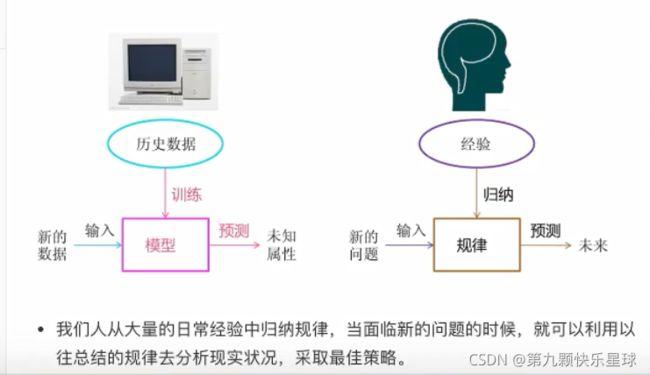
一 机器学习,深度学习能做什么
二 机器学习的定义
三 机器学习算法分类
分类,回归的区别:
分类,回归问题的共同点:
线性回归
线性回归的损失(损失函数/cost/成本函数)
四 深度学习中超参数的介绍:
1什么是超参数,参数和超参数的区别:
2神经网络中包含哪些超参数:
3为什么要进行超参数调优:
4超参数上的重要顺序:
1)学习率,损失函数上的可调参数:在网络参数、优化参数、正则化参数中最重要的超参数可能就是学习率了。学习率直接控制着训练中网络梯度更新的量级,直接影响着模型的有效容限能力;
2)批样本数量:
3)优化器超参数、权重衰减系数、dropout和网络参数
五 CNN网络的搭建:
1)全连接层
2)卷积层
3)池化层
4) 理解全连接,卷积,池化层三者的关系
5)激活函数
什么是激活函数?
为什么需要激活函数?
一 机器学习,深度学习能做什么
传统预测
图像识别
自然语言处理
二 机器学习的定义
三 机器学习算法分类
1分类算法
2回归算法
分类,回归的区别:
1输出变量的不同:
定量输出称为回归,或者说是连续变量预测;
定性输出称为分类,或者说是离散变量预测。
举个例子:
预测明天的气温是多少度,这是一个回归任务;
预测明天是阴、晴还是雨,就是一个分类任务。
2应用场景不同:
回归问题通常是用来预测一个值,如预测房价、未来的天气情况等等,例如一个产品的实际价格为500元,通过回归分析预测值为499元。
分类问题是用于将事物打上一个标签,通常结果为离散值。例如判断一幅图片上的动物是一只猫还是一只狗,分类通常是建立在回归之上,分类的最后一层通常要使用softmax函数进行判断其所属类别。分类并没有逼近的概念,最终正确结果只有一个,错误的就是错误的,不会有相近的概念。
分类,回归问题的共同点:
线性回归
1)定义与公式
线性回归(Linear regression)是利用回归方程(函数)对一个或多个自变量(特征值)和因变量(目标值)之间关系进行建模的一种分析方式。
特点:只有一个自变量的情况称为单变量回归,多于一个自变量情况的叫做多元
回归
通用公式:h(w)=W1X1+W2X2+W3X3...+b=w^T+b
其中w,x可以理解为矩阵
那么怎么理解呢?我们来看这个例子
期末成绩:0.7×考试成绩+0.3×平时成绩
上面这个例子,我们看到特征值与目标值之间建立了一个关系,这个关系可以理解为线性模型。
2)线性回归当中线性模型有两种,一种是线性关系,另一种是非线性关系。
线性回归的损失(损失函数/cost/成本函数)
四 深度学习中超参数的介绍:
1什么是超参数,参数和超参数的区别:
区分两者最大的一点就是是否通过数据来进行调整,模型参数通常是由数据来驱动调整,超参数则不需要数据来驱动,而是在训练前或者训练中人为的进行调整的参数。例如卷积核的具体核参数就是指模型参数,这是有数据驱动的。而学习率则是人为来进行调整的超参数。这里需要注意的是,通常情况下卷积核数量、卷积核尺寸这些也是超参数,注意与卷积核的核参数区分。
2神经网络中包含哪些超参数:
通常可以将超参数分为三类:网络参数、优化参数、正则化参数。
网络参数:可指网络层与层之间的交互方式(相加、相乘或者串接等)、卷积核数量和卷积核尺寸、网络层数(也称深度)和激活函数等。
优化参数:一般指学习率(learning rate)、批样本数量(batch size)、不同优化器的参数以及部分损失函数的可调参数。
正则化:权重衰减系数,丢弃法比率(dropout)
3为什么要进行超参数调优:
寻找到全局最优解(或者相比更好的局部最优解)
使模型尽量拟合到最优
4超参数上的重要顺序:
1)学习率,损失函数上的可调参数:在网络参数、优化参数、正则化参数中最重要的超参数可能就是学习率了。学习率直接控制着训练中网络梯度更新的量级,直接影响着模型的有效容限能力;
2)批样本数量:
批样本是一次训练所选取的样本数。Batch Size的大小影响模型的优化程度和速度。同时其直接影响到GPU内存的使用情况,假如你GPU内存不大,该数值最好设置小一点。
(1)、通过并行化提高内存的利用率。就是尽量让你的GPU满载运行,提高训练速度。
(2)、适当Batch Size使得梯度下降方向更加准确。
3)优化器超参数、权重衰减系数、dropout和网络参数
这些参数重要性放在最后并不等价于这些参数不重要。而是表示这些参数在大部分实践中不建议过多尝试,比如优化器超参数和权重衰减系数,选择默认推荐值即可。dropout通常会在全连接层之间使用防止过拟合。增加网络层数可以提高模型有效性,但一般情况下会选择固定网络层数,对样本数量和质量、层之间的关系进行调优,有大量的硬件资源支持可以在网络深度上进行进一步调整。
五 CNN网络的搭建:
1)全连接层
全连接层(fully connected layers,FC)在整个卷积神经网络中起到“分类器”的作用。如果说卷积层、池化层和激活函数层等操作是将原始数据映射到隐层特征空间的话,全连接层则起到将学到的“分布式特征表示”映射到样本标记空间的作用。
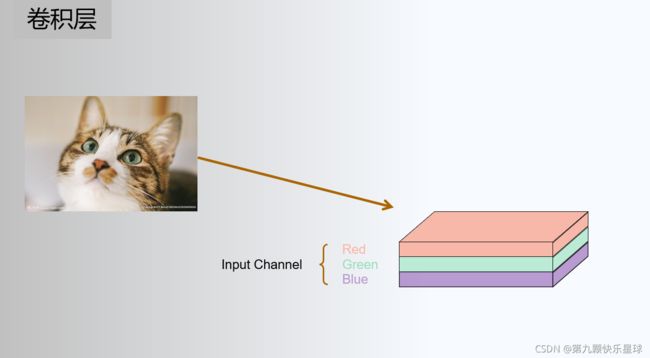
2)卷积层
卷积神经网络中每层卷积层(Convolutional layer)由若干卷积单元组成,每个卷积单元的参数都是通过反向传播算法最佳化得到的。卷积运算的目的是提取输入的不同特征,第一层卷积层可能只能提取一些低级的特征如边缘、线条和角等层级,更多层的网路能从低级特征中迭代提取更复杂的特征。
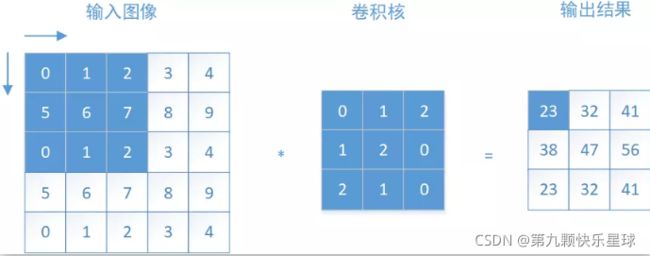
把输入图像看作是一个n维矩阵,然后拿一个m*m维(m
移动过程中涉及一个重要的概念--步长(stride),它的意思就是"扫描"过程中每次移动几个像素,如果步长stride=1,那么从左至右、从上之下逐个像素的移动。
上图二维卷积运算为例,输入图像为一个5*5的矩阵,卷积核为3*3,以步长stride=1进行卷积运算,在左上角这个窗口每个对应元素先相乘再相加,即
0*0+1*1+2*2+5*1+6*2+7*0+0*2+1*1+2*0=23
以这种方式逐个窗口进行计算,就得到图中等号右边的输出结果。
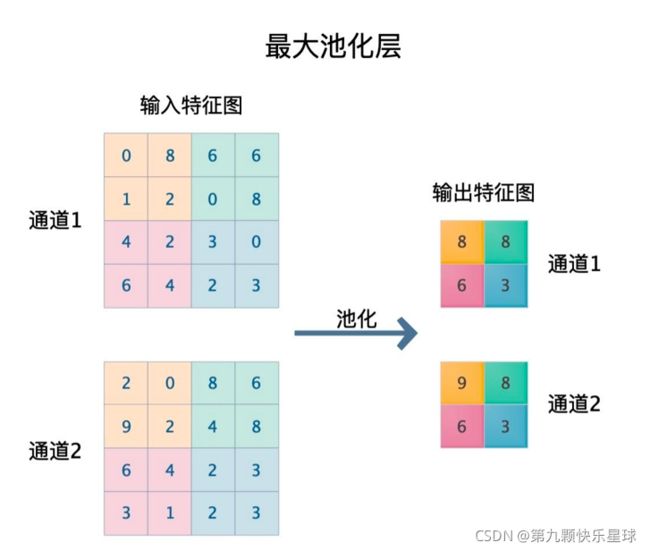
3)池化层
池化层和卷积层一样,是CNN模型必不可少的一个部分,在很多卷积层后会紧跟一个池化层,而且在统计卷积神经网络时,池化层是不单独称为网络层的,它与卷积层、激活函数、正则化同时使用时共同称为1个卷积层。
池化层又称为下采样或者欠采样,它的主要功能是对于特征进行降维,压缩数据和参数量,避免过拟合,常用的池化方式有两种:
-
最大池化
-
平均池化
以最大池化为例介绍一下它是怎么实现的
和卷积层类似,池化层也有窗口和步长的概念,其中步长在里面的作用也是完全相同的,就是窗口每次移动的像素个数。
池化层的窗口概念和卷积层中是不同的,在卷积层中每移动到一个窗口,对应的卷积核和输入图像做卷积运算。而在池化层中,窗口每移动到一个位置,就选择出这个窗口中的最大值输出,如果是平均池化就输出这个窗口内的平均值。
4) 理解全连接,卷积,池化层三者的关系
从卷积网络谈起,卷积网络在形式上有一点点像咱们找对象谈恋爱(滑稽jpg)。卷积核的个数相当于对象候选人,图像中不同的特征(如性格 三观 颜值 身材等)会激活不同的“对象候选人”(卷积核)。
池化层(仅指最大池化)起着类似于“合票”的作用,不同特征在对不同的“对象候选人”有着各自的喜好。
全连接相当于是“普选”。所有被选出的“对象候选人”,需要对最终结果进行“选择”,全连接保证了receiptive field 是整个图像,即图像中各个部分(所谓所有“对象候选人”),都有对最终结果影响的权利。
还可以理解为:
假设你是一只狼,你的任务是找小绵羊。你的视野还比较窄,只能看到很小一片区域。当你找到一只小绵羊之后,你不知道你找到的是不是全部的小棉羊,所以你们全部的狼开了个会,把所有的小棉羊都拿出来分享了。全连接层就是这个狼大会~
5)激活函数
什么是激活函数?
对于神经网络,一层的输入通过加权求和之后输入到一个函数,被这个函数作用之后它的非线性性增强,这个作用的函数即是激活函数。
为什么需要激活函数?
对于神经网络而言,如果没有激活函数,每一层对输入进行加权求和后输入到下一层,直到从第一层输入到最后一层一直采用的就是线性组合的方式,根据线性代数的知识可以得知,第一层的输入和最后一层的输出也是呈线性关系的,换句话说,这样的话无论中加了多少层网络都没有任何价值,这是第一点。如果没有激活函数,输入和输出是呈线性关系的,但是现实中很多模型都是非线性的,通过引入激活函数可以增加模型的非线性,使得它更好的拟合非线性空间。