DBSCAN聚类学习-matlab代码撰写-2022-08-10
对于dbscan的学习,来自于以下的博主,非常的感谢
DBSCAN详解_皮卡丘的情绪的博客-CSDN博客_dbscan
所以,博主再这里不阐述dbscan的原理了,直接上代码,所有注释都有,可以直接吃和改进:
1 dbscan在matlab中的实现
% dbscan学习
% 模拟数据
clc
clear
rng('default') % For reproducibility
% Parameters for data generation
N = 300; % Size of each cluster
r1 = 0.5; % Radius of first circle
r2 = 5; % Radius of second circle
theta = linspace(0,2*pi,N)';
X1 = r1*[cos(theta),sin(theta)]+ rand(N,1);
X2 = r2*[cos(theta),sin(theta)]+ rand(N,1);
data = [X1;X2]; % Noisy 2-D circular data set
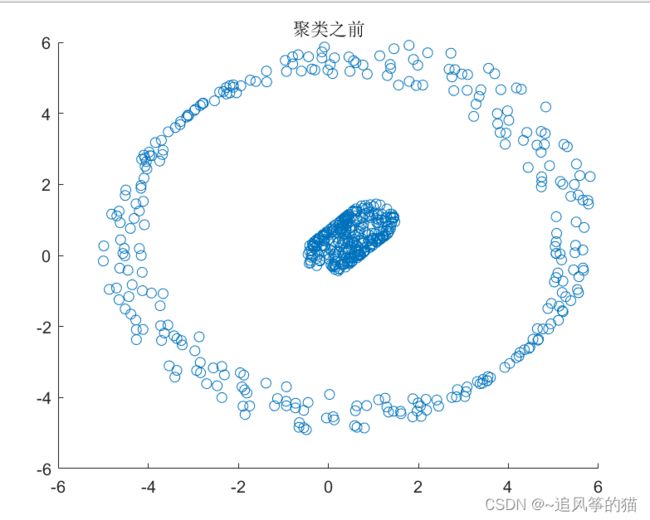
scatter(data(:,1),data(:,2))
title('聚类之前')
% 设置参数,esp为领域大小,minpt为最小数量点
esp = 1;
minpt = 5;
% 计算点与点之间的距离,三维点同样适用
% pdist2(a,b),计算a中的点到b中的点的距离
% 第一行为a中第一个点到b中所有点的距离
% d = pdist2(data,data);
% Rgion = find(d(1,:)<=esp);
% rangesearch功能为搜索esp内的所有点
d = rangesearch(data,data,esp);
% 计算数据的大小
[n,m] = size(data);
% 设置访问标记
vist = zeros(n,1);
% 设置聚类组
idx = zeros(n,1);
% 设置聚类标签
lab = 0;
% 循环整个点组
for i = 1:n
% 是否第i个点已经被访问过,如果被访问过,就下一个点
% 如果没有被访问过,则继续处理
if vist(i,:) == 0
% 访问设置为1,没被访问为0
vist(i,:) = 1;
% 提取集合
neig = d{i};
% 判断是否满足阈值条件,即是否可以聚类
if numel(neig)>=minpt
% 如果密度可以聚类,创建类的标签
lab = lab+1;
% 为当前点归类
idx(i,:) = lab;
% 设置循环指针
k = 1;
% 进行密度可达寻找
while neig
% 寻找d集合中第i个点的esp邻域的第k个点
j = neig(k);
% 判断当前点是否被访问过
if vist(j,:) == 0
% 如果没被访问,则设置为1,即访问过
vist(j,:) = 1;
% 提取新的集合
neig2 = d{j};
% 判断当前点的领域点数量是否满足条件
if numel(neig2)>=minpt
% 满足条件,即将当前点的所有邻域点纳入第i点集合
neig = [neig,neig2];
neig = unique(neig);
end
else
neig(k) =[];
end
% 如果第j个点没有从属类,则归类
if idx(j,:) == 0
idx(j) = lab;
end
% 指针往前,如果指针的值大于neig集合的点的个数
% 说明没有密度可达的点,则结束循环
% k = k+1;
% if k > numel(neig)
% break
% end
end
end
end
end
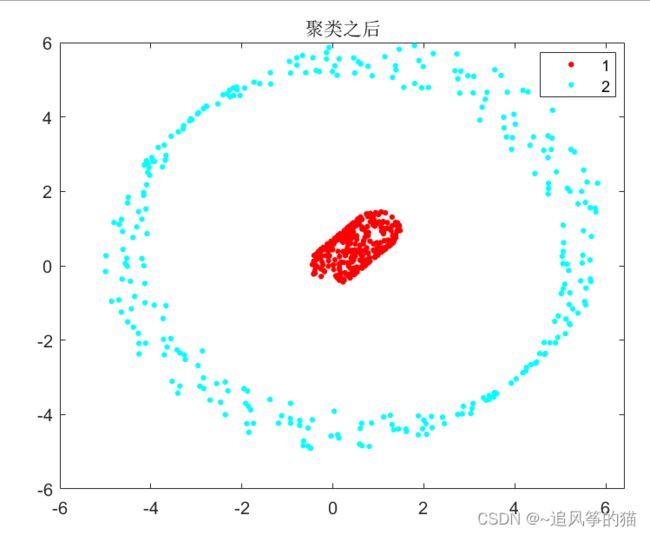
gscatter(data(:,1),data(:,2),idx);
title('聚类之后')
结果如下:
自写得dbscan运行很慢,比起matlab自带得功能,慢上十倍,2w数量的点云分割,需要1分钟。
不知道问题出在哪里,已经看了很多博主写的代码了,仍然没有解决,痛苦。
2 matlab自带dbscan的功能
matlab2019b自带dbscan函数,应用如下:
idx = dbscan(X,epsilon,minpts)
idx = dbscan(X,epsilon,minpts,Name,Value)
idx = dbscan(D,epsilon,minpts,'Distance','precomputed')
[idx,corepts] = dbscan(___)
clc
clear
rng('default') % For reproducibility
% Parameters for data generation
N = 300; % Size of each cluster
r1 = 0.5; % Radius of first circle
r2 = 5; % Radius of second circle
theta = linspace(0,2*pi,N)';
X1 = r1*[cos(theta),sin(theta)]+ rand(N,1);
X2 = r2*[cos(theta),sin(theta)]+ rand(N,1);
data = [X1;X2]; % Noisy 2-D circular data set
scatter(data(:,1),data(:,2))
title('聚类之前')
axis on
idx = dbscan(data,1,5);
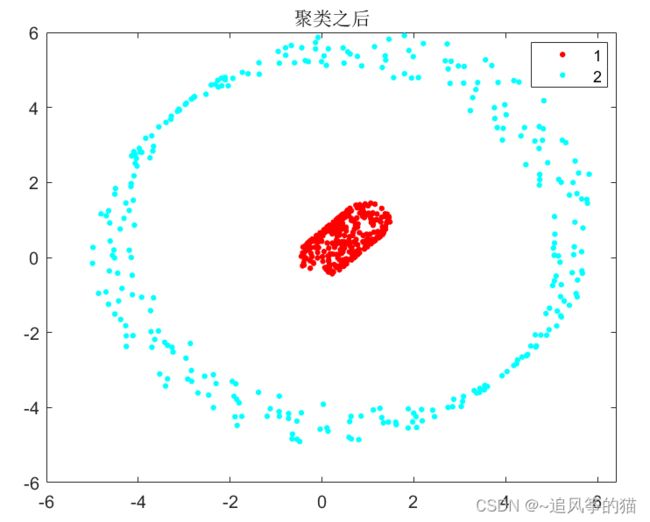
gscatter(data(:,1),data(:,2),idx);
title('聚类之后')结果如下:
效果的差异不明显
此外博主写的k均值和欧式距离聚类如下:
Kmean(k均值聚类)学习-2022-08-09_~追风筝的猫的博客-CSDN博客
Matlab点云欧式距离聚类-2021-12-06_~追风筝的猫的博客-CSDN博客_matlab 欧式聚类
点云-均值漂移-均适用_点云均值漂移-数据集文档类资源-CSDN下载
3、 8月11更新,dbscan代码小优化,运行速度提升
借鉴于以下博主:
DBSCAN的理解和matlab实现_尼古拉斯.贝叶斯基的博客-CSDN博客_dbscan matlab
修改了密度可达的集合合并,比之前的运行速度快了十倍,但是比起matlab自带的函数还是慢着很多很多,不过已经很好了,感觉基本得到了解决。不列结果了,基本一样
clc
clear
rng('default') % For reproducibility
% Parameters for data generation
N = 300; % Size of each cluster
r1 = 0.5; % Radius of first circle
r2 = 5; % Radius of second circle
theta = linspace(0,2*pi,N)';
X1 = r1*[cos(theta),sin(theta)]+ rand(N,1);
X2 = r2*[cos(theta),sin(theta)]+ rand(N,1);
data = [X1;X2]; % Noisy 2-D circular data set
scatter(data(:,1),data(:,2))
% clear
% clc
% % 模拟数据
% [X,Y,Z] = sphere(100);
% loc1 = [X(:),Y(:),Z(:)];
% loc2 = 2*loc1;
% ptCloud = pointCloud([loc1;loc2]);
% pcshow(ptCloud)
% title('Point Cloud')
% data = ptCloud.Location;
tic
% 设置参数,esp为领域大小,minpt为最小数量点
esp = 1;
minpt = 5;
% 计算点与点之间的距离,三维点同样适用
% pdist2(a,b),计算a中的点到b中的点的距离
% 第一行为a中第一个点到b中所有点的距离
% d = pdist2(data,data);
% Rgion = find(d(1,:)<=esp);
% rangesearch功能为搜索esp内的所有点
d = rangesearch(data,data,esp);
% 计算数据的大小
[n,m] = size(data);
% 设置访问标记
vist = zeros(n,1);
% 设置聚类组
idx = zeros(n,1);
% 设置聚类标签
lab = 0;
% 循环整个点组
for i = 1:n
% 是否第i个点已经被访问过,如果被访问过,就下一个点
% 如果没有被访问过,则继续处理
if vist(i,:) == 0
% 访问设置为1,没被访问为0
vist(i,:) = 1;
% 提取集合
neig = d{i};
% 判断是否满足阈值条件,即是否可以聚类
if numel(neig)>=minpt
% 如果密度可以聚类,创建类的标签
lab = lab+1;
% 为当前点归类
idx(i,:) = lab;
% 设置循环指针
k = 1;
% 进行密度可达寻找
while true
% 寻找d集合中第i个点的esp邻域的第k个点
j = neig(k);
% 判断当前点是否被访问过
if vist(j,:) == 0
% 如果没被访问,则设置为1,即访问过
vist(j,:) = 1;
% 提取新的集合
neig2 = d{j};
% 判断当前点的领域点数量是否满足条件
if numel(neig2)>=minpt
% 满足条件,即将当前点的所有邻域点纳入第i点集合
neig2 = setdiff(neig2,neig);
neig = [neig,neig2];
end
% else
% neig(k) =[];
end
% 如果第j个点没有从属类,则归类
if idx(j,:) == 0
idx(j) = lab;
end
% 指针往前,如果指针的值大于neig集合的点的个数
% 说明没有密度可达的点,则结束循环
k = k+1;
if k > numel(neig)
break
end
end
end
end
end
toc
% pcshow(data,idx)
gscatter(data(:,1),data(:,2),idx);