元强化学习 论文理解 MAESN
论文理解 MAESN
- 主要思想
- 具体实现
-
- 元学习框架
- 带有隐层状态的策略
- 元学习更新
- 小结
主要思想
这篇文章主要关注于如何加强对于新任务的探索性。
动机:
以往探索策略在很大程度上是任务无关的,因为它们旨在提供良好的探索,而不利用任务本身的特定结构。然而,与现实世界交互的智能代理可能需要学习许多任务,而不仅仅是一个任务,在这种情况下,可以使用先前的任务来通知如何执行新任务中的探索。
首先,同样的策略必须表示高度探索性的行为,并非常快速地适应最佳行为,这对于动作分布的典型时不变表示来说变得非常困难。
其次,许多当前的元RL方法旨在学习整个“学习算法”,如RNN。它们通过RNN的单次前向传递快速适应,但与从头学习相比,这大大限制了它们的渐近性能,因为与标准RL方法不同,RNN通常不对应于收敛的迭代优化过程。
方法:
我们的目标是通过设计一种元RL算法来解决这两个挑战,该算法通过遵循策略梯度来适应新任务,同时还将学习到的结构化随机性注入潜在空间,以实现有效的探索。我们的算法,我们称之为带结构噪声的模型不可知探索(MAESN),使用先验经验来初始化策略,并学习潜在的探索空间,从中可以对时间上连贯的结构化行为进行采样,从而产生随机的、由先验知识告知的、比随机噪声更有效的探索策略。重要的是,明确训练政策和潜在空间,以快速适应具有政策梯度的新任务。由于自适应是通过遵循策略梯度来执行的,我们的方法至少实现了与从头开始学习相同的渐近性能(并且通常表现得更好),而结构化随机性允许随机化但有任务意识的探索。
具体实现
元学习框架
MAESN将结构随机性与MAML相结合。MAESN是一种基于梯度的元学习算法,它不仅通过扰动动作,而且通过学习的潜在空间引入随机性。策略和潜在空间都经过元学习训练,以快速适应新任务。当在元测试时间解决新任务时,从每个试验的潜在空间中生成不同的样本,提供结构化和时间相关的随机性。然后通过策略梯度更新使潜在变量的分布适应任务。
带有隐层状态的策略
这里引入了隐层状态以加强探索。具体而言就是对于每一个任务 τ i \tau_{i} τi生成一组均值与方差( μ i , σ i \mu_{i}, \sigma_{i} μi,σi)。通过对于每一个任务的均值与方差进行采样可以得到一个隐层状态变量 z i z_{i} zi。这里 z i z_{i} zi是对于每个任务生成一次的。通过将 z i z_{i} zi加入到状态输入的方式,等价于对于每个任务加入了一个噪声以增强探索,而一个任务的隐状态噪声来自于同一组分布,这样增强了任务间的认知与探索。
隐状态示意图如下:
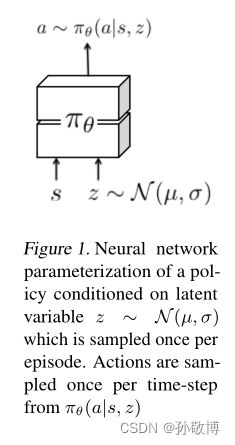
而这里要求( μ i , σ i \mu_{i}, \sigma_{i} μi,σi)是可导的,因此这里使用了VE中的方法。 z = μ + ϵ ∗ σ z = \mu + \epsilon * \sigma z=μ+ϵ∗σ,其中 ϵ \epsilon ϵ是随机的,这样可以对于( μ i , σ i \mu_{i}, \sigma_{i} μi,σi)求梯度。
同时这里同样在TRPO损失的基础上加入了一个希望分布 N ( μ , σ ) N(\mu, \sigma) N(μ,σ)与标准高斯分布尽可能相似的KL散度损失。
其中为了计算关于µ,σ的梯度,我们需要通过采样操作z反向传播,使用似然比或重新参数化技巧。似然比更新为
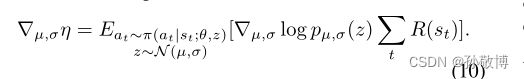
元学习更新
因此元学习更新时对于 θ \theta θ 和( μ i , σ i \mu_{i}, \sigma_{i} μi,σi)( i ∈ T i \in \Tau i∈T)进行更新,更新公式如下:
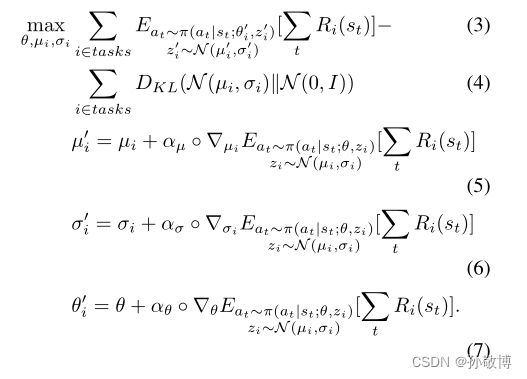
更新的流程图如下:

因此元学习的伪代码为:

小结
总结一下这篇文章,个人认为它主要使用了MAML的框架,其贡献在于加入了一个针对于任务的隐状态作为噪声,以鼓励考虑任务类别的探索。
隐状态的实现主要通过对于每个任务初始化一个可学习的高斯分布均值方差 ( μ , σ ) (\mu, \sigma) (μ,σ),通过从 N ( μ , σ ) N(\mu, \sigma) N(μ,σ)中采样获得隐状态z。将z 与转台一起输入网络模型中或的动作。
进行更新时,损失函数加入了一个 N ( μ , σ ) N(\mu, \sigma) N(μ,σ)与标准高斯分布KL散度的损失以加强近似性。更新参数时除了更新网络参数外也需要更新 ( μ , σ ) (\mu, \sigma) (μ,σ)。