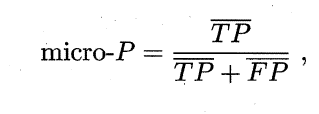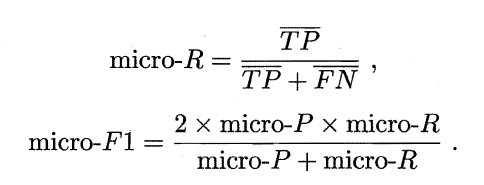DataWhale西瓜书第一第二章学习笔记
视频绪论
人工智能
机器学习
深度学习
计算机视觉
自然语言处理
推荐系统
高等数学:会求偏导数
线性代数:会矩阵运算
概率论与数理统计:随机变量是什么
内容定位:西瓜书里的算法的公式推导
本科数学视频:张宇考研数学系列
第一章
1.2 基本术语
数据集(data set):数据记录的集合
示例(instance)/样本(sample):每条记录是关于一个事件或对象的描述
属性(attribute)/特征(feature):反映事件或对象在某方面的表现或性质的事项
属性值(attribute value):属性上的取值
属性空间(attribute space)/样本空间(sample space)/输入空间:属性张成的空间
例如:色泽 根蒂 敲声 作为三个坐标轴 张成一个用于描述西瓜的三维空间,每个西瓜都可以在这个空间中找到自己的坐标位置。空间中的每个点对应一个坐标向量
特征向量(feature vector):一个示例
令 D = { X1, X2, … , Xm}表示包含m个示例的数据集,每个示例由d个属性描述(上面的西瓜数据使用了3个属性),则每个示例Xi = (Xi1;Xi2;…;Xid)是d维样本空间X中的一个向量,xi ∈Χ, 其中 Xij是Xi在第j个属性上的取值(例如上述第3个西瓜在第2个属性上的值是“硬挺”),d称为样本xi的维数(dimensionality)
学习(Learning)/训练(training):从数据中学得模型地过程
通过执行某个学习算法来完成
训练数据(training data):训练过程中使用的数据
训练样本(training sample):每个样本
训练集(training set):训练样本组成的集合
假设(hypothesis):学得模型对应了关于数据的某种潜在的规律
真相/真实(ground-truth):潜在规律本身
学习过程为了找出或逼近真相
学习器(Learner):有时将模型称为/ 看作学习算法在给定数据和参数空间上的实例化
预测(prediction):获得训练样本的结果信息
标记(label):比如好瓜(自定义对数据进行分类)
样例(example):拥有了标记信息的示例
标记空间(label space)/输出空间 用(xi, yi)表示第i个样例,其中yi ∈ Y是示例xi的标记,Y是所有标记的集合
分类(classification):预测的是离散值 比如 好瓜 坏瓜
回归(regression):预测的是连续值 比如成熟度 0.95 0.37
二分类(binary classification):任务 只涉及两个类别
正类(positive class)
反类(negative class)
多个类别(multi-class classification)
预测任务是希望通过对训练集{(x1, y1), (x2, y2), … , (xm, ym)}进行学习,建立一个从输入空间Χ到输出空间Y的映射 f : Χ⟼Υ 。对二分类任务,通常令Υ={−1, +1}或{0,1}
对多分类任务,|Υ| >2;
对回归任务, Υ = R R为实数集
测试(testing):使用学习的模型进行预测的过程
测试样本(testing sample):被预测的样本
学得 f 后, 对测试例 x,可得到其预测标记y = f(x)
聚类(clustering):训练集中的个体分成若干组,每组称为一个簇(cluster)
潜在概念:浅色瓜 本地瓜 深色瓜 外地瓜
监督学习(supervised learning):分类和回归
无监督学习(unsupervised learning):聚类
泛化(generalization)能力:学得模型适用于新样本的能力
分布(distribution)D: 通常假设样本空间中全体样本服从一个未知,我们获得的每个样本都是独立地从这个分布上采样获得的
独立同分布(independent and identically distributed 简称i.i.d)
训练样本越多,获得的关于的D的信息越多,越有可能通过学习获得具有强泛化能力的模型
布尔概念学习;“是”“不是”表示为0/1布尔值的目标概念的学习

对于没见过的数据;如何判断?
把学习过程看作一个在所有假设(hypothesis)组成的空间中进行搜索的过程,搜索目标:
找到与训练集匹配(fit)的假设,即能够将训练集中的瓜判断正确的假设。假设的表示一旦确定,假设空间及其规模大小就确定了
也许色泽无论取什么值都可以,用通配符“*”来表示。
考虑极端情况:有可能好瓜的概念根本不存在 用∅表示这个假设。
每个样本的特征分别有322种可能取值,面临的假设空间规模大小为4×3×3×1=37

模型的评估与选择
2.1 经验误差与过拟合
错误率(error rate):分类错误的样本数占样本总数的比例
m个样本中有a个样本分类错误,错误率E=a/m,精度1-a/m(accuracy)
误差(error):学习器的实际预测输出与样本的真实输出之间的差异
训练误差(training error)/经验误差(empirical error):学习器在训练集上的误差
泛化误差(generalization error):新样本上的误差
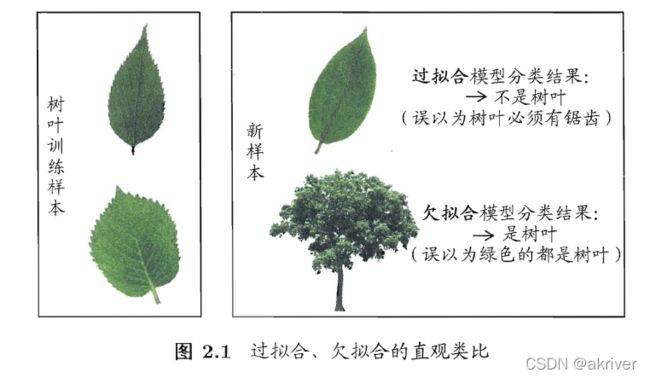
过拟合(overfitting):把训练样本自身的一些特点当作所有潜在样本都具有的一般性质,导致泛化性能下降
学习能力过于强大,把训练样本所包含的不太一般的特性都学到了
欠拟合(underfitting):一般性质尚未学好
学习能力低下;在决策树学习中扩展分支,在神经网络学习中增加训练轮数
模型选择(model selection):用哪一个学习算法,使用哪一种参数配置
2.2 评估方法
使用一个测试集来测试学习器对新样本的判别能力,然后以测试集上的测试误差(testing error)作为泛化误差的近似。通常假设测试样本也是从样本真实分布中独立同分布采样而得。
测试集与训练集尽量互斥。
避免乐观情况
只有一个包含m个样例的数据集D = {(x1, y1),(x2, y2), …,(xm,ym)}
对D进行适当处理,从中产生出训练集S和测试集T
2.2.1 留出法
Hold-out,将数据集D划分为两个互斥的集合,其中一个作为训练集S,另一个作为测试集T,即D = S ∪T,S∩T=∅ 。在S上训练出模型后,用T来评估其测试误差,作为对泛化误差的估计。
二分类任务为例,D包含1000个样本,划分为S包含700个样本,T包含300个样本,用S进行训练后,如果模型在T上有90个样本分类错误,那么其错误率为(90/300)X100%=30%,精度为70%。
*:保持数据分布一致性,避免引入额外的偏差对最终结果产生影响;分类任务中至少保持样本的类别比例相似。
- 例如通过对D 进行分层采样而获得含70% 样本的训练集S 和含30% 样本的测试集T, 若D 包含500 个正例、500 个反例,则分层采样得到的S 应包含350 个正例、350 个反例?而T 则包含150 个正例和150 个反例;若S、T 中样本类别比例差别很大,则误差估计将由于训练/测试数据分布的差异而产生偏差。
- 在使用留出法时,采用若干次随机划分,重复进行实验评估后取平均值作为留出法的评估结果。进行100次随即划分,每次产生一个训练/测试集用于实验评估,100次后就得到100个结果,留出法返回的则是这100个结果的平均。
- 将大约2/3~4/5的样本用于训练,剩余样本用于测试。
2.2.2 交叉验证法
Cross validation划分为k个大小相似的互斥子集。
![]()
每个子集Di尽可能保持数据分布一致性,即从D中通过分层采样得到。每次用k-1个子集的并集作为训练集,余下的那个子集作为测试集;就可获得k组训练/测试集,从而可进行k次训练和测试,最终返回的是这k个测试结果的均值。
稳定性和保真性很大程度取决于k的取值,通常把交叉验证法称为“k折交叉验证“(k-fold cross validation)
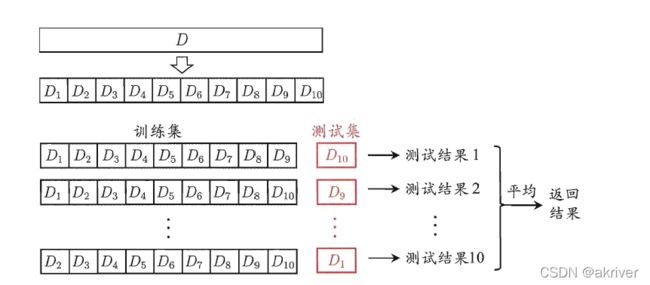
为减小因样本划分不同而引入的差别,k折交叉验证通常要随机使用不同的划分重复p次,最终的评估结果是这p次k折交叉验证结果的均值,常见的有10次10折交叉验证
数据集D中包含m个样本,令k=m,则得到了交叉验证法的一个特例:留一法(Leave-One-Out LOO)
2.2.3 自助法
Bootstrapping 比较好的解决方案,以bootstrap sampling为基础。给定包含m个样本的数据集D,对它进行采样产生数据集D’:
每次随即从D中挑选一个样本,拷贝放入D’,再将该样本放回初始数据集D中,使得该样本在下次采样时仍有可能被采到;过程重复执行m次后,就得到了包含m个样本的数据集D’

通过自助采样,初始数据集D中约36.8%样本未出现在采样数据集D’中,可将D’用作训练集,D\D’用作测试集;
实际评估的模型与期望评估的模型都使用m个训练样本,仍有数据总量约1/3,没在训练集中出现的样本用于测试,测试结果,亦称”包外估计(out-of-bag-estimate)“
2.2.4 调参与最终模型
-
Parameter tuning 假定算法有3个参数,每个参数仅考虑5个候选值,对每一组训练/测试集就有5^3=125个模型需考察。模型在训练过程中使用了所有m个样本,才是最终提交给用户的模型。
-
模型额评估与选择中用于评估测试的数据集常称为验证集(validation set)
-
研究对比不同算法的泛化性能时,测试集上的判别效果来估计模型在实际使用时的泛化能力,而把训练数据另外划分为训练集和验证集,基于验证集上的性能来进行模型选择和调参。
2.3 性能度量
Performance measure 预测任务:

回归任务;均方误差(mean squared error):
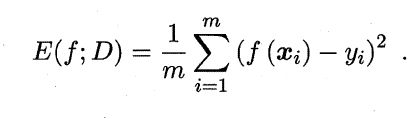
数据分布D和概率密度函数p(⋅),均方误差可描述为:
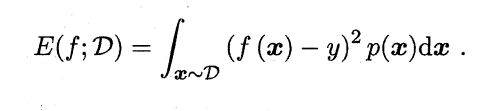
对于数据分布D和概率密度函数p(⋅);
错误率:
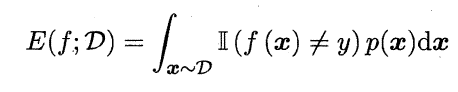
精度:

2.3.2 查准率,查全率与F1
信息检索;用户感兴趣:Precision与Recall
二分类问题:True positive, False positive, True negative, False negative
Confusion matrix:

查准率P与查全率R:
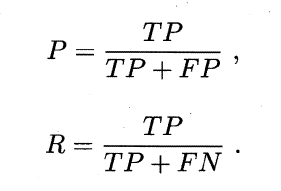
查准率-查全率曲线,简称P-R曲线:

A完全包住C;学习器A的性能优于学习器C
Break-Event Point BEP
学习器C的BEP是0.64,基于BEP的比较,学习器A优于B
比较BEP,更常用F1度量

信息检索:查准率更重要
逃犯信息检索:查全率更重要
F1的一般度量形式Fβ



宏查准率(macro-P),宏查全率(macro-R)以及相应的宏F1(macro-F1):


微查准率(micro-P)微查全率(micor-R)微F1(micro-F1):