分位数回归--基于R

分位数回归

分位数回归是估计一组回归变量X与被解释变量Y的分位数之间线性关系的建模方法。以往的回归模型实际上是研究被解释变量的条件期望。而人们也关心解释变量与被解释变量分布的中位数、分位数呈何种关系。它最早由Koenker和Bassett(1978)提出。OLS回归估计量的计算是基于最小化残差平方。分位数回归估计量的计算也是基于一种非对称形式的绝对值残差最小化。

当我们使用0.9分位数回归，重新得出新函数图像如左图上：
可以看到，这比起普通的回归分析，就能进一步显示出y的变化幅度其实是增大了。所谓的0.9分位数回归，就是希望回归曲线之下能够包含90%的数据点（y），这也是分位数的概念。

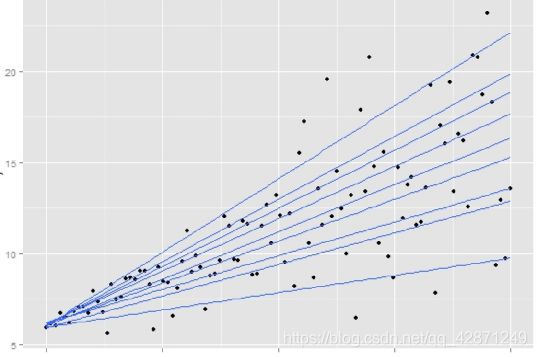
当然，我们仅仅得到0.9分位数回归曲线是不够的，进一步的我们可以画出不同的分位数回归曲线，这样才能能更加明显地反映出，随着x的增大，y的不同范围的数据是不同程度地变化的。

分位数回归优点

（1）能够更加全面的描述被解释变量条件分布的全貌，而不是仅仅分析被解释变量的条件期望（均值），也可以分析解释变量如何影响被解释变量的中位数、分位数等。不同分位数下的回归系数估计量常常不同，即解释变量对不同水平被解释变量的影响不同。
（2）中位数回归的估计方法与最小二乘法相比，估计结果对离群值则表现的更加稳健，而且，分位数回归对误差项并不要求很强的假设条件，因此对于非正态分布而言，分位数回归系数估计量则更加稳健。

案例

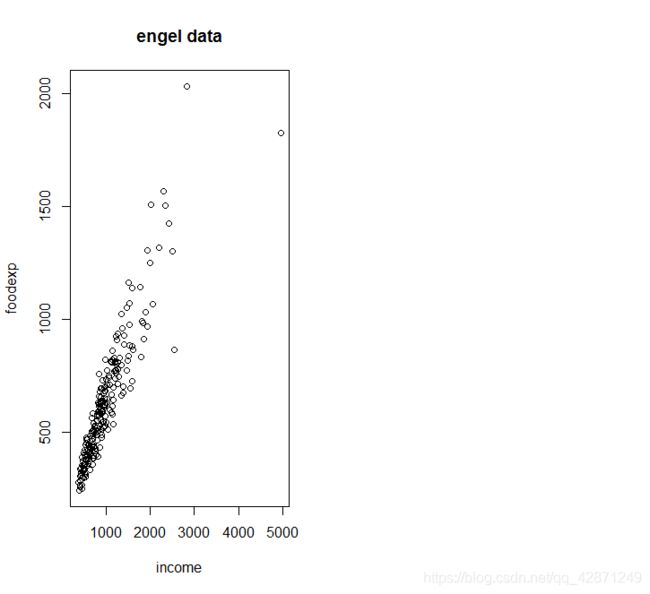
用的是R自带的数据集engel
library(quantreg)#使用包quantreg
data(engel)
head(engel)
income foodexp
1 420.1577 255.8394
2 541.4117 310.9587
3 901.1575 485.6800
4 639.0802 402.9974
5 750.8756 495.5608
6 945.7989 633.7978
包含自变量income ，因变量foodexp

建模使用函数rq
rq(foodexp~income,tau = 1:49/50,data=engel)
其中tau为自己设置的分位数，当设置为-1时，所有分位数的结果全部显示出来
rq1 = rq(foodexp~income,data = data,tau = -1)
summary.rq(rq1)
rq1$sol[4:5,]#4,5行是各个分位数的截距、斜率

完整代码：
先看tau取值 1:49/50
library(quantreg);data(engel)
head(engel)
plot(summary(rq(foodexp~income,tau = 1:49/50,data=engel)))

library(quantreg);data(engel)
par(mfrow=c(1,2))
plot(foodexp ~ income, data = engel, main = “engel data”)#产生散点图
taus <- c(.15, .25, .50, .75, .95, .99)#选择6个tau参数
rqs <- as.list(taus)#构造和taus一样多元素的list来存储回归结果
for(i in seq(along = taus)) { #对每个tau做分位数回归并画图
rqs[[i]]=rq(foodexp~income, tau=taus[i],data=engel)
lines(engel$income, fitted(rqs[[i]]), col = i+1)}
legend(“bottomright”, paste("tau = ", taus), inset = .04,
col = 2:(length(taus)+1), lty=1)

#重复上面(把foodexp换成log10(foodexp)):
plot(log10(foodexp) ~ log10(income), data = engel,
main = “engel data (log10 - tranformed)”)
for(i in seq(along = taus)) {
rqs[[i]]=rq(log10(foodexp)~log10(income),
tau=taus[i],data=engel)
lines(log10(engel$income), fitted(rqs[[i]]), col = i+1)}
legend(“bottomright”, paste("tau = ", taus), inset = .04,
col = 2:(length(taus)+1), lty=1)

#tau=-1:取(0,1)中的密集的tau(这里271个回归, 结果在z中):
library(quantreg);data(engel);attach(engel)
z <- rq(foodexp~income,tau=-1,engel)#最密集的回归
#下面取贫富两个income值(x值):
x.poor=quantile(income,.05);x.rich=quantile(income,.95)
#下面算出贫富的income对所有tau斜率和截距的拟合值(各271个):
qs.poor <- c(c(1,x.poor)%*%zKaTeX parse error: Expected 'EOF', got '#' at position 11: sol[4:5,])#̲用公式x'b计算拟合值 qs.…sol[4:5,])#%5分位点算出的271个y值
#上面z$sol[4:5,]为z中相应于不同分位数的斜率和截距ps<-z$sol[1,]#tau值
ps.wts <- (c(0,diff(ps)) + c(diff(ps),0)) / 2
ap <- akj(qs.poor, z=qs.poor, p = ps.wts)#akj: 自适应核密度估计
ar <- akj(qs.rich, z=qs.rich, p = ps.wts)
#ap$dens与ar$dens为两个密度估计
#下面是画图程序
par(mfrow = c(1,2))
plot(c(ps,ps),c(qs.poor,qs.rich), type=“n”, xlab = expression(tau), ylab = “foodexp”)
plot(stepfun(ps,c(qs.poor[1],qs.poor)),do.points=F,add=T)
plot(stepfun(ps,c(qs.rich[1],qs.rich)),do.points=F,add=T,lty=2)
legend(“topleft”, c(“poor”,“rich”), lty = c(1,2))
plot(c(qs.poor,qs.rich),c(ap$dens,ar$dens),type=“n”,xlab= “FoodExpenditure”, ylab= “Density”)
lines(qs.poor, ap$dens)lines(qs.rich,ar$dens,lty=2)
legend(“topright”, c(“poor”,“rich”), lty = c(1,2))