单纯形法；大M法；两阶段法

线性规划问题的标准形式

规定的标准形式为：

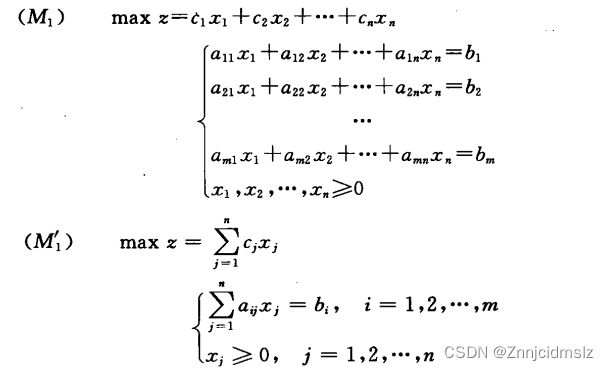
在标准形式中规定各约束条件的右端项bi>0，否则等式两端乘以“一1”。当某一个bi=0时，表示出现退化，这点将在以后讨论。

1.单纯形法

不等式约束中只有≤时，可以用单纯形法。

1.1定义

可行解：满足约束条件和非负约束的解。

最优解：可行解中使目标函数达到最大值的解。

基本解：令非基变量为0，再求线性方程组得到的唯一解。

基本可行解：满足非负约束的基本解。

1.2思路

先找到一个初始的基本可行解，判定其是否为最优解，若否，则转换到相邻的基本可行解，并使目标函数值不断增大，一直找到最优解为止。

1.3计算步骤

①将问题化为标准形，在约束方程的系数矩阵中找到或构造单位矩阵，以单位矩阵为基，求出初始基本可行解；列出单纯形表。

②进行最优性检验

若存在检验数＞0，则不是最优解；若多个检验数＞0，则把较大的那个检验数所对应的变量作为入基变量（进入到基变量中去）。

③转换基可行解

④重复2和3，直到计算结束。

1.4Python求解

import numpy as np
def pivot():
    #1.选择入基变量：index_intoB（求入基变量的列索引）
    l = list(matrix[0][:-1]) #list()转换为列表；matrix[0][:-1]返回第一行（最后一列之外）的数值
    index_intoB = l.index(max(l)) #取检验数的最大值列索引; l.index(a)是返回列表中最左端的a的下标

    #2.选择出基变量：index_outB（求行索引）
    col_inB = [] #建立一个空列表，然后将bi/aij的值放进去，再求min值
    for i in range(b_num):
        if matrix[i][index_intoB] == 0: #若aij为0，则不参与bi/aij的计算
            col_inB.append(0.)
        else:
            col_inB.append(matrix[i][-1] / matrix[i][index_intoB])#计算bi/aij
    m = [x for x in col_inB[1:] if x > 0] #找出col_inB中大于0的值；对于col_inB[1:]中的每个x，如果x>0为真，则将其添加到m中
    index_outB = col_inB.index(min(m)) #取bi/aij的最小值(0除外)作为出基变量；返回的是最小值在col_inB列表中的索引

    #3.将基变量列表中进行新旧基的替换
    indexes_B[index_outB - 1] = index_intoB #index_outB-1为出基变量在基变量列表中的索引，因矩阵第一行是目标函数c，约束矩阵A从第二行开始
    cur_cell_to1 = matrix[index_outB][index_intoB] #主元素的值
    #作为基，其特点为：由单位向量所构成，因此：
    matrix[index_outB] /= cur_cell_to1 #该行全部除以主元素的值，使其为1，即该行标准化

    #4.通过行变换将其他行的非零元去除
    #注意：这一操作对第一行也执行了，将表达式中的新基变量也给消除，用其他非基变量来表示！第一行的最后一个数值极为z0，即目标函数值！
    n = [x for x in range(b_num) if x != index_outB] #对于range(b_num)中的每个x，如果x不等于index_outB，则将其添加到列表n中
    for row in n:
        cur_cell_to0 = matrix[row][index_intoB]
        matrix[row] -= cur_cell_to0 * matrix[index_outB]#先算乘法再减法

def solve():#5.判断检验数是否小于等于0
    flag = True
    while flag:
        if max(list(matrix[0][:-1])) <= 0:  #直至所有检验数小于等于0
            flag = False
        else:
            pivot()

def printSol():
    for i in range(c_num - 1):
        if i in indexes_B:
            print("x" + str(i) + "=%.2f" % matrix[indexes_B.index(i) + 1][-1])
        else:
            print("x" + str(i) + "=0.00")
    print("objective is %.2f" % (-matrix[0][-1]))

matrix = np.loadtxt("G:\data2.txt", dtype=float)
(b_num, c_num) = matrix.shape #matrix.shape可以快速读取矩阵的形状
indexes_B = list(range(c_num - b_num, c_num - 1)) #基变量列表
solve()
printSol()

1.5调用scipy包求解

'''
4 3 0 0 0 0
2 1 1 0 0 10
1 1 0 1 0 8
0 1 0 0 1 7
'''

from scipy import optimize
import numpy as np
c = np.array([4,3])
A_ub = np.array([[2,1],[1,1],[0,1]]) #不等式约束参数矩阵
B_ub = np.array([10,8,7]) #不等式约束参数向量
res = optimize.linprog(-c,A_ub,B_ub) #c为价值向量，代表规划最小值，最大值需改为-c；
print(res)

2.大M法

一些线性规划问题在化为标准形后，约束条件系数矩阵不存在单位矩阵，就需要在约束条件中添加人工变量，构造一个新的线性规划问题。

2.1思路

①将约束条件转化为标准形式（加入松弛变量、剩余变量）

②引入人工变量a，构造基B，找出基变量

③目标函数中引入Ma，M为趋近于正无穷的任意大的数

④制表，构造初试基本可行解

⑤利用检验数判断是否达到最优

参考课程

3.两阶段法

对于大M法，在用计算机求解时，只能在计算机内给M赋值一个尽可能大的数字，由于计算机计算时取值上的误差，可能使计算结果发生错误。

为了克服这个困难，可以对添加人工变量后的线性规划问题分两个阶段来计算，称两阶段法。

思路

• 阶段一：判断原线性规划问题是否有基本可行解

决策变量：原问题未知变量+松弛变量+剩余变量+人工变量
目标函数：令人工变量的系数为1或-1，其余所有变量系数都为0
约束条件：原问题加入人工变量后的约束条件

①构建初始单纯形表
②求检验数并判断
③出基入基变换
④重复②③，直到求出最优解（最终的基变量中无人工变量，且最优解为0，则原问题有基本可行解；反之无）

• 阶段二：第一阶段有基本可行解的情况下，进行阶段二

决策变量：原问题未知变量+松弛变量+剩余变量
目标函数：原问题的目标函数
约束条件：将第一阶段最终单纯形表中的人工变量列去掉

将第一阶段得到的最优解作为第二阶段的初试基本可行解，从第一阶段的最终单纯形表出发继续迭代。