算法积分0042算法笔记——【随机化算法】计算π值和计算定积分
最近研究算法积分,稍微总结一下,以后继续补充:
1、盘算π值
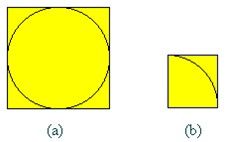
问题描述
设有一半径为r的圆及其外切四边形。向该正方形随机地投掷n个点。设落入圆内的点数为k。由于所投入的点在正方形上平均分布,因而所投入的点落入圆内的概率为 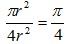 。所以当n足够大时,k与n之比就逼近这一概率。从而
。所以当n足够大时,k与n之比就逼近这一概率。从而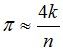 。
。
程序详细代码如下:
//随机化算法 用随机投点法盘算π值
#include "stdafx.h"
#include "RandomNumber.h"
#include <iostream>
using namespace std;
double Darts(int n);
int main()
{
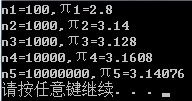
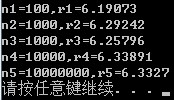
int n1 = 100,n2 = 1000,n3 = 1000,n4 = 10000,n5 = 10000000;
cout<<"n1="<<n1<<",π1="<<Darts(n1)<<endl;
cout<<"n2="<<n2<<",π2="<<Darts(n2)<<endl;
cout<<"n3="<<n3<<",π3="<<Darts(n3)<<endl;
cout<<"n4="<<n4<<",π4="<<Darts(n4)<<endl;
cout<<"n5="<<n5<<",π5="<<Darts(n5)<<endl;
return 0;
}
//用随机投点法盘算π值
double Darts(int n)
{
static RandomNumber dart;
int k = 0;
for(int i=1; i<=n; i++)
{
double x = dart.fRandom();
double y = dart.fRandom();
if((x*x + y*y)<=1)
{
k++;
}
}
return 4*k/double(n);
}
程序运行结果如图:
2、盘算定积分
例:设f(x)=x^2,求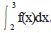
解: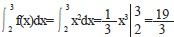
1)随机投点法盘算定积分
基本思想是在矩形区域上随机平均的投点实现。本算法的基本思想是在积分区间上随机平均的产生点, 即在[a,b]上随机平均的取点, 求出由这些点产生的函数值的算术平均值, 再乘以区间宽度, 便可解出定积分得近似解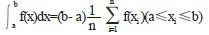 。
。
算法详细代码如下:
//随机化算法 用随机投点法盘算定积分
#include "stdafx.h"
#include "RandomNumber.h"
#include <iostream>
using namespace std;
double Darts(int n,double a,double b);
double f(double x);
int main()
{
int n1 = 100,n2 = 1000,n3 = 1000,n4 = 10000,n5 = 10000000;
double a = 2.0,b = 3.0;
cout<<"n1="<<n1<<",r1="<<Darts(n1,a,b)<<endl;
cout<<"n2="<<n2<<",r2="<<Darts(n2,a,b)<<endl;
cout<<"n3="<<n3<<",r3="<<Darts(n3,a,b)<<endl;
cout<<"n4="<<n4<<",r4="<<Darts(n4,a,b)<<endl;
cout<<"n5="<<n5<<",r5="<<Darts(n5,a,b)<<endl;
return 0;
}
/*
* 基本思想是在矩形区域内随机平均投点,求出由这些点
* 产生的函数值的算术平均值,再乘以区间宽度,便可得
* 出定积分的近似解
*/
double Darts(int n,double a,double b)
{
static RandomNumber dart;
double sum = 0.0;
for(int i=0; i<n; i++)
{
double x = (b-a)*dart.fRandom() + a;//产生[a,b)之间的随机数
sum = sum + f(x);
}
return (b-a)*sum/n;
}
double f(double x)
{
return x*x;
}
程序运行结果如图:
2)概率法法盘算定积分
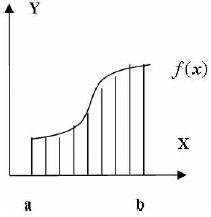
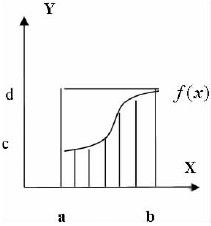
设f:[a,b]→[c,d]连续函数(如图2 所示), 则由曲线y=f(x)以及x 轴和直线x=a,x=b 围成的面积由定积分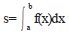 给出。根据几何概型可知
给出。根据几何概型可知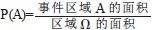 。假设向矩形区域随机平均的投镖n 次, 落入阴影为K次, 又设M为x=a、x=b、y=c、y=d 所围成的矩形面积, s 为定积分面积,则
。假设向矩形区域随机平均的投镖n 次, 落入阴影为K次, 又设M为x=a、x=b、y=c、y=d 所围成的矩形面积, s 为定积分面积,则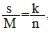 , 所以s= k/n×M。
, 所以s= k/n×M。
算法详细代码 如下:
//随机化算法 用概率法盘算定积分
#include "stdafx.h"
#include "RandomNumber.h"
#include <iostream>
using namespace std;
double Darts(int n,double a,double b,double d);
double f(double x);
int main()
{
int n1 = 100,n2 = 1000,n3 = 1000,n4 = 10000,n5 = 10000000;
double a = 2.0,b = 3.0;
double d = f(b);
cout<<"n1="<<n1<<",r1="<<Darts(n1,a,b,d)<<endl;
cout<<"n2="<<n2<<",r2="<<Darts(n2,a,b,d)<<endl;
cout<<"n3="<<n3<<",r3="<<Darts(n3,a,b,d)<<endl;
cout<<"n4="<<n4<<",r4="<<Darts(n4,a,b,d)<<endl;
cout<<"n5="<<n5<<",r5="<<Darts(n5,a,b,d)<<endl;
return 0;
}
/*
* f 为积分函数, n 为投镖
* 总数, a,b 为积分区间, c,d 为函
* 数f 的值域的端点值
*/
double Darts(int n,double a,double b,double d)
{
static RandomNumber dart;
int k = 0;
for(int i=0; i<n; i++)
{
double x = (b-a)*dart.fRandom() + a;//产生[a,b)之间的随机数
double y = d * dart.fRandom();
if(y<=f(x))
{
k++;
}
}
return d*(b-a)*k/n;
}
double f(double x)
{
return x*x;
}
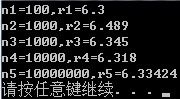
程序运行结果如图:
文章结束给大家分享下程序员的一些笑话语录: 火车
一个年轻的程序员和一个项目经理登上了一列在山里行驶的火车,他们发现 列车上几乎都坐满了,只有两个在一起的空位,这个空位的对面是一个老奶 奶和一个年轻漂亮的姑娘。两个上前坐了下来。程序员和那个姑娘他们比较 暧昧地相互看对方。这时,火车进入山洞,车厢里一片漆黑。此时,只听见 一个亲嘴的声音,随后就听到一个响亮的巴掌声。很快火车出了山洞,他们 四个人都不说话。
那个老奶奶在喃喃道, “这个年轻小伙怎么这么无礼, 不过我很高兴我的孙女 扇了一个巴掌”。
项目经理在想,“没想到这个程序员居然这么大胆,敢去亲那姑娘,只可惜那 姑娘打错了人,居然给打了我。”
漂亮的姑娘想,“他亲了我真好,希望我的祖母没有打疼他”。
程序员坐在那里露出了笑容, “生活真好啊。 这一辈子能有几次机会可以在亲 一个美女的同时打项目经理一巴掌啊”
--------------------------------- 原创文章 By
算法和积分
---------------------------------