深度学习笔记(一)
计算机视觉:
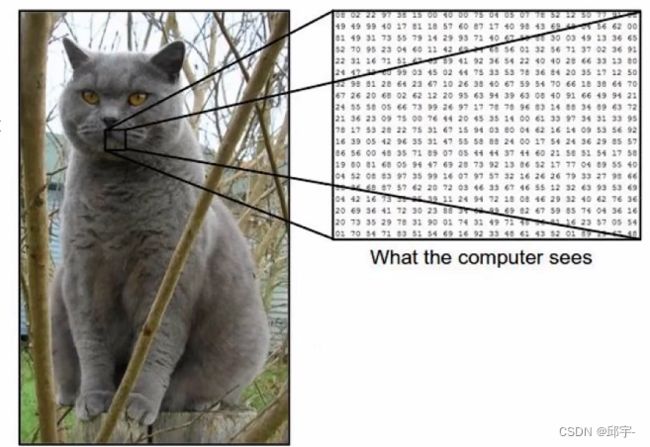
图像表示:计算机眼中的图像
一张图像被表示成三维数组(三维矩阵)的形式,每个像素的值从0到255,图像中数值越大表示该点越亮,图像中数值越小表示该点越暗;
例如:300*100*3,其中300是图像的长,100是宽,3表示颜色通道的数目,一张JPG图像或者RGB图像,其颜色通道数都是3;
计算机视觉面临的挑战:照射角度改变、形状改变、部分遮蔽、背景混入
机器学习常规套路:1、收集数据并给定标签;2、训练一个分类器;3、测试、评估;
神经网络基础:
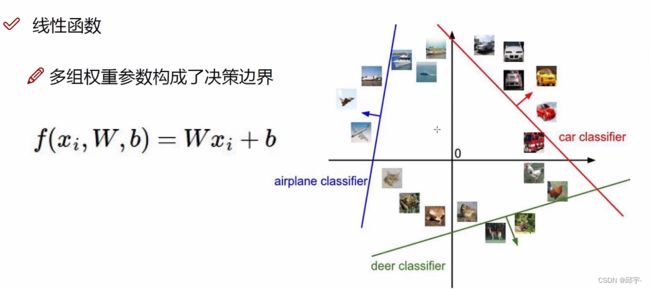
1.线性函数(得分函数):从输入--->输出的映射
每个像素点对于得分结果的作用不一样,有些像素点对于它是猫这个类别的得分是促进作用(比如猫的眼睛、耳朵),有的像素点对于它是猫这个类别起到抑制作用(比如背景),不同像素点对应于当前这个类别的重要程度不一样,3072个像素点要对应3072个权重参数,权重参数越大,表示这个像素点对分类结果越重要
权重参数起决定性影响因素,偏置参数起微调作用
计算方法:
权重参数矩阵是通过多次训练不断优化出来的,它是变化的。神经网络在整个生命周期当中所做的事情就是,什么样的W权重参数能更适合于数据去做当前这个任务,就怎么样去改变W,因为w中的值会对最终结果产生决定性影响。
权重参数控制着整个决策边界的走势,偏置参数起微调作用
2.损失函数
损失函数等于0时代表没有损失,此处1是一个![]() ,相当于一个容忍程度,也就是正确类别得分至少得比错误类别得分高
,相当于一个容忍程度,也就是正确类别得分至少得比错误类别得分高![]() 以上才是没有损失的。正确类别的损失函数的值越小,代表分类越正确。
以上才是没有损失的。正确类别的损失函数的值越小,代表分类越正确。
![]() 是惩罚系数,
是惩罚系数,![]() 值越大,代表着不希望过拟合,把变异的部分值给去掉。
值越大,代表着不希望过拟合,把变异的部分值给去掉。
3.Softmax分类器
概率值越接近于1,越没有损失;越接近于0,损失越大。
4.前向传播
![]()
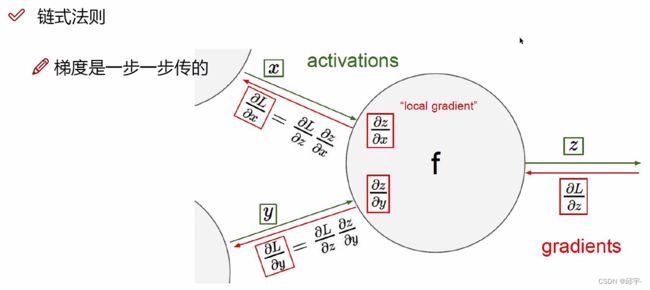
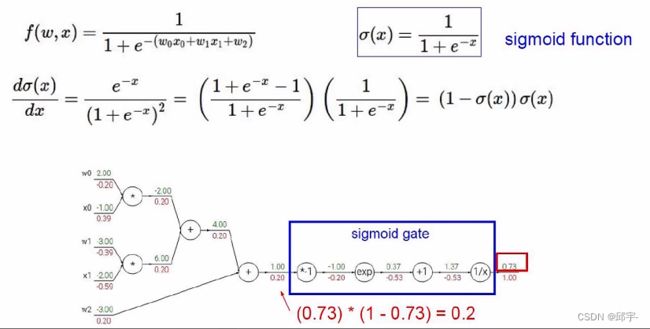
5.反向传播计算方法
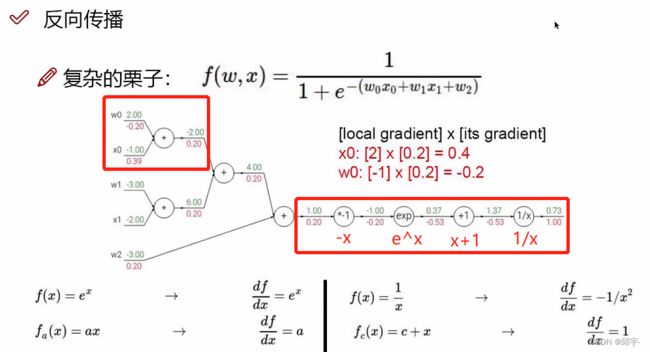
首先,在1/x处,根据![]() ,将x=1.37代入,得到
,将x=1.37代入,得到![]() ,然后-0.53乘以1/x后面的梯度值1.00得到此处的梯度值等于-0.53;
,然后-0.53乘以1/x后面的梯度值1.00得到此处的梯度值等于-0.53;
然后来到x+1处,根据![]() ,然后1乘以x+1后面的梯度值-0.53得到此处的梯度值-0.53;
,然后1乘以x+1后面的梯度值-0.53得到此处的梯度值-0.53;
接着,在![]() 处,根据
处,根据![]() ,将x=-1.00代入,得到
,将x=-1.00代入,得到![]() ,然后0.37乘以
,然后0.37乘以![]() 后面的梯度值-0.53得到此处的梯度值-0.20;
后面的梯度值-0.53得到此处的梯度值-0.20;
最后,在-x处,根据![]() ,然后-1乘以-x后面的梯度值-0.20得到此处的梯度值0.20。
,然后-1乘以-x后面的梯度值-0.20得到此处的梯度值0.20。
对于前面的部分,同样按照反向传播方法来计算:
假设![]() ,根据
,根据![]() 得到
得到![]() ,然后-1.00乘以q后面的梯度值0.20得到此处的梯度值为-0.20;
,然后-1.00乘以q后面的梯度值0.20得到此处的梯度值为-0.20;
根据![]() 得到
得到![]() ,然后2.00乘以q后面的梯度值0.20得到此处的梯度值为0.40。
,然后2.00乘以q后面的梯度值0.20得到此处的梯度值为0.40。
例如图中方框里面的部分可以看作一个整体,
将![]() 代入得到
代入得到![]() ,然后0.2乘以门函数后面得梯度值1.00,得到此处的梯度值0.20
,然后0.2乘以门函数后面得梯度值1.00,得到此处的梯度值0.20
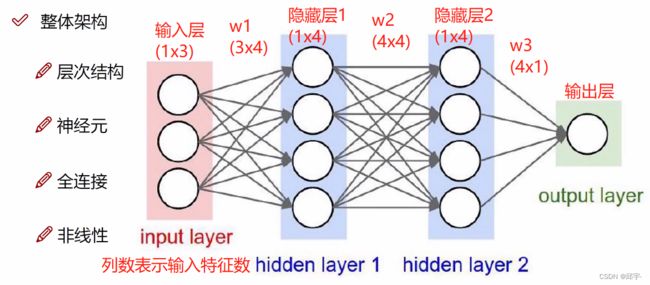
6.神经网络整体架构
层次结构:对数据一层一层的做变换,![]()
神经元:即数据量或者叫做矩阵大小
全连接:输入层中的每个特征点都和隐层中的每个点连在一起
非线性:x与w1组合完后先做非线性变换后再与w2组合,然后又要进行非线性变换后再与w3组合,即非线性操作是加在每一步矩阵计算之后的,假设非线性变换函数是max(0,x)
 隐层1的作用:将原始输入信息转换为计算机认识的数据,把原始的三个特征变换为四个特征
隐层1的作用:将原始输入信息转换为计算机认识的数据,把原始的三个特征变换为四个特征
隐层2的作用:在w1的基础上再进行提取
神经网络结果的好坏取决于w1、w2、w3做得好不好
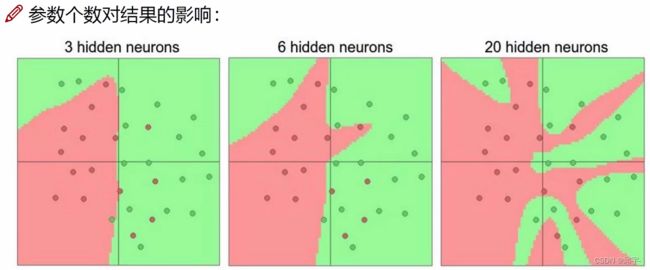
神经元个数对结果的影响:理论上,神经元越多,得到的过拟合程度越大,在训练集上得到的效果越好。但是相对来说,运行速度也会比较慢。
7.正则化与激活函数
正则化的作用:
因为计算损失的时候,是![]() ,所以越小的
,所以越小的![]() 值,越符合训练集的结果,同时,其过拟合程度也越大。通常我们需要的是测试集上的效果比较好的,训练集的效果即便达到100%也没什么用,实际看的是测试集。
值,越符合训练集的结果,同时,其过拟合程度也越大。通常我们需要的是测试集上的效果比较好的,训练集的效果即便达到100%也没什么用,实际看的是测试集。
参数个数对结果的影响:其实就是你想由输入的几个特征,得到多少维的其他的特征
比较常见的权重参数矩阵的大小:64,128,256,512,1024,也即参数的个数。
神经元越多,过拟合风险越大。一般情况下尽量不选过拟合的,尽可能在不过拟合的前提下把任务做好。
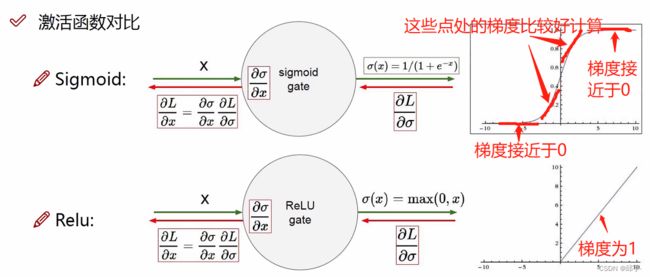
神经网络经过了一组权重参数计算完之后要进行非线性变换,激活函数就列出来几种常见的非线性变换。
sigmoid函数存在的问题:在靠近左右两边的时候,梯度约等于0。约等于0的梯度代表不进行更新、不进行传播。例如:(((xw1)w2)w3)w4,往前传的过程中,如果w3等于0,则w2、w1必然为0.这就是sigmoid函数带来的问题。因为在sigmoid函数中,一旦数值较大,或者数值较小,在进行求导的过程当中,得到的结果可能就不好,会出现梯度消失现象。也就是由于个别层的影响,使得梯度最后计算完之后没了
Relu函数的特点:小于0的部分都等于0,大于0的部分都等于本身,梯度全为1;
不存在梯度消失现象
8.神经网络过拟合解决办法
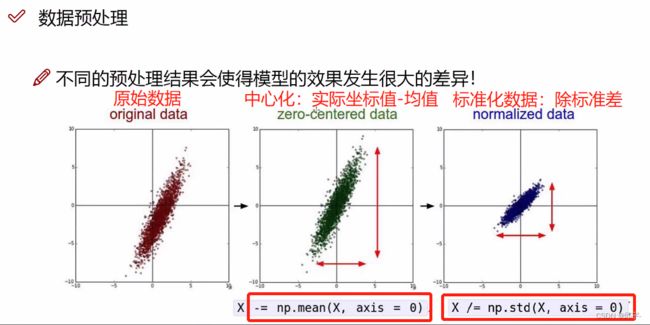
中心化:实际坐标值-均值,得到一个以原点为中心,对称的结果
进行各个维度的放缩或扩充:除标准差
 初始化:先给一个随机的值,然后在训练过程中,反向传播要重新计算参数值。
初始化:先给一个随机的值,然后在训练过程中,反向传播要重新计算参数值。
在进行初始化时,w里面的值是比较小的,学习率Learning Rate也是比较小的。
神经网络中最大的问题是整个网络架构太复杂了,层数比较多,每一层中神经元个数也比较多,会造成整个神经网络过拟合风险特别大。
要让过拟合风险降低,一定程度上要削减整个网络的性能。要舍弃其中一部分,来增强网络抗拒过拟合的能力。
Drop-Out:在神经网络的训练阶段,在每一层、每一次随机的选择固定比例(比如50%)的一部分神经元,将其去掉,让网络架构变得简洁。(测试阶段不需要)